Вычисление периодических решений неавтономного уравнения Дюффинга методом малого параметра

Одним из хорошо известных методов нахождения периодических решений нелинейных дифференциальных уравнений является метод малого параметра, предложенный А. Пуанкаре [4] и получивший свое развитие в последующих работах [5; 6].

В приведенных работах при вычислении периодического решения методом малого параметра, как правило, ограничиваются вычислениями первого или второго приближения в разложении искомого решения в ряд по малому параметру. В предлагаемой работе на основе автоматизации в математическом пакете Maple процесса нахождения приближений   2тг- периодического решения неавтономного уравнения Дуффинга приведены результаты по вычислению приближений до третьего порядка включительно. Разработанный программный модуль в пакете Maple позволяет по наперед заданному произвольному числу приближений найти эти приближения.

Вычисление периодического решения неавтономного уравнения Дуффинга вдали от резонанса. Рассмотрим уравнение Дуффинга в виде [5]

x + а2х = Л sin t + у ^х3,

где собственная частота а - отличное от нечетного целого вещественное число, i - малый параметр, Л и у - некоторые вещественные параметры. Уравнение (1) будем называть возмущенным уравнением для случая вдали от резонанса.

Приведем результат работы программного модуля для п = 3, реализующего алгоритм вычисления методом малого параметра 2л-периодического решения неавтономного уравнения Дуффинга при условии, что значение собственной частоты находится вдали от резонансных значений.

Представим периодическое решение уравнения (1) в виде

x(t) = x0(t) + lx1(t) + 12х2(0 + 13х3(с) + o(i3).

Подставляя выражение (2) в уравнение (1), приравнивая коэффициенты при одинаковых степенях малого параметра μ в левой и правой частях и пренебрегая слагаемыми порядка o(i3), получим систему уравнений

Х0 + )2х0 = Л sin t,

Х₂ + а²х₂ = 3ух 0 х 1 ,

Х1 + ш2х1 = ух03,

Х3 + )2х3 = 3ух^х2 + 3ух0х2.

Последовательно решая уравнения системы (3) в пакете Maple, получим

x0(t) = Л, sin t, х1(С) = B1 sin t + B3 sin 3t, х3(С) = D1 sin t + D3 sin 3t +

+D5 sin 5t + D7 sin 7t, уЛ3

^B3 = ^— 4()² — 1)³()² — 9),

3у2Л5(5а2 — 29)

’ 16(а2 —1)6(а2 —9)2,

x2(t) = C1 sin t + C3 sin 3t + C5 sin 5t, где

л — Л          n      3уЛ3

1    = О7—7,      B1 = 4()2 _ 1)4 ,

_  3у2Л5(5а2 — 41)      _

C1 = 8()2 — 1)7()2 — 9) , C3 =

3у2Л5

r =______________________

C 16(а2 —1)5(а2 —9)()2 —25),

D i

3у 3Л7 (35)4 — 550)2 + 2243) 16(а2 — 1)10(а2 — 9)2

9у3Л7(7а6 — 255а4 + 2361а2 — 6721) 16()2 — 1)10()2 — 9)2()2 — 25)

n      3у3Л7(7ы4- 188^2 + 901)

D5 = 16(^2 - 1)8(w2 - 9)2(^2 - 25)2,

n                     3у3Л7(бо2 - 13)

D7 = -ТбС^'-л)7^^'-!)2^^          ■

Первое уравнение системы (3) будем называть невозмущенным уравнением для случая вдали от резонанса.

В качестве приближения порядка о(/б3) к 2тт-периодическому решению уравнения (1) возьмем

5з (t) = Хо (t) + ^X1 (t) + ^2X2 (t) + ^3Хз (t),                           (5)

Приближения фазовых траекторий уравнения (1) будем строить как параметрические кривые r(t) = (S₃(t),S₃(t)), t £ [0,2^].

Графики периодических решений и фазовые траектории уравнения Дуффинга вдали от резонанса. Поскольку в этом параграфе рассматривается не резонансный случай, то в качестве собственной частоты выберем, например, ^ = 2.

Приведем графики 2я-периодических решений и фазовых траекторий уравнения (1) при Л = 1 и у = 6 и различных значениях параметра ^ (рис. 1, 2).

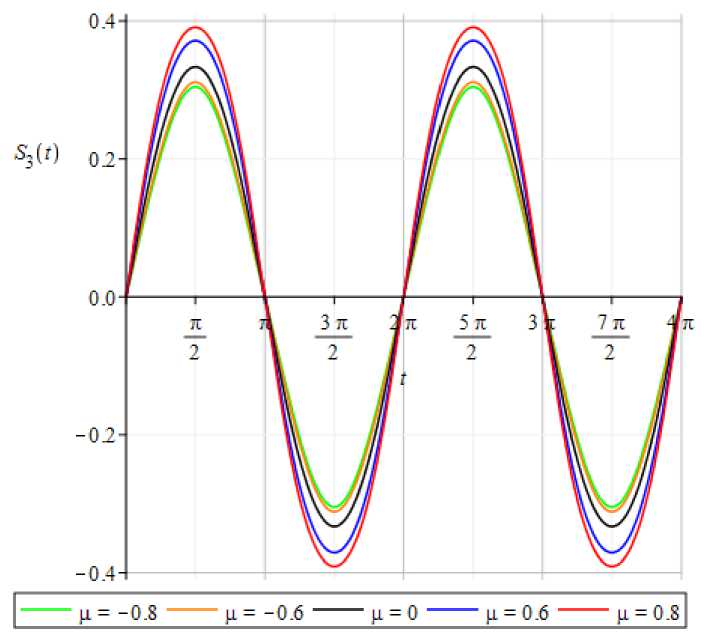
Рис. 1. Графики 2я- периодических решений уравнения (1) в случае отсутствия резонанса при различных значениях параметра ^.

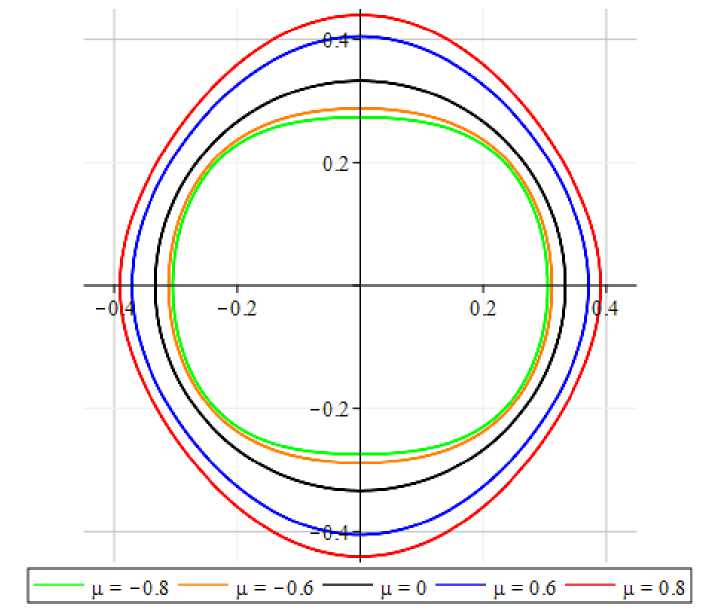
Рис. 2. Графики фазовых траекторий уравнения (1) в случае отсутствия резонанса при различных значениях параметра /л.

Вычисление периодического решения неавтономного уравнения Дуффинга при резонансе. Рассмотрим случай, когда собственная частота ш равна единице или меньше ее на

некоторый малый параметр. Тогда согласно [5] представим собственную частоту ш в виде

ш2 = 1 + Ь/,

• и рассмотрим два случая:

• 1)    резонанс: ш² = 1, Ь = 0;

• 2)    вблизи резонанса: ш² = 1 + /, Ь = 1, / < 0.

Тогда в первом случае уравнение (1) примет вид х + х = /(ух³ + А 1 sin t),

во втором случае получим

х + х = /(-х + ух3 + А1 sin t).

Здесь, А = / А 1 . Уравнения (7) и (8) будем называть возмущенным уравнением для

случаев 1 и 2, соответственно. Уравнение

z + z = 0,

- невозмущенным уравнением для случаев 1 и 2, соответственно.

В виду громоздкости формул, выражающих аналитическую зависимость приближений периодических решений от параметров у и Л1, приведем результаты работы программного модуля для приближенного вычислений 2я-периодических решений с точностью o(g3) при значениях у = 6 и Л1 = 1 для случаев 1) ш2 = 1, Ъ = 0

S3(t) = -0,6057 sin t + g(-0,1389 • 10-1 sin t - 0,4166 • 10-1 sin 3t) +

+g2(0,6372 • 10-2 sin t + 0,1434 • 10-1 sin 3t - 0,2866 • 10-2 sin 5t) +

+g3(-0,2679 • 10-2 sin t - 0,4470 • 10-2 sin 3t + 0,1447 • 10-2 sin 5t -

-0,1971 • 10-3sin7t),

и случая 2) ш2 = 1 + g, Ъ = 1, g < 0

S3(t) = -0,7265 sin t + g(-0,2789 • 10-1 sin t - 0,7189 • 10-1 sin 3t) +

+g2(0,1448 • 10-1 sin t + 0,2 542 • 10-1 sin 3t - 0,7117 • 10-2 sin 5t) +

+g3(-0,6310 • 10-2 sin t - 0,6766 • 10-2 sin 3t + 0,3783 • 10-2 sin 5t -

-0,7042 • 10-3sin7t).

Погрешность вычислений составляет 10 4.

Графики периодических решений и фазовых траекторий уравнения Дуффинга при резонансе. Построим графики 2я-периодических решений и фазовых траекторий уравнения (1) для случаев 1) ш² = 1, Ъ = 0 (рис. 3, 4) и 2) ш² = 1 + g, Ъ = 1, g < 0 (рис. 5, 6)

при различных значениях параметра g.

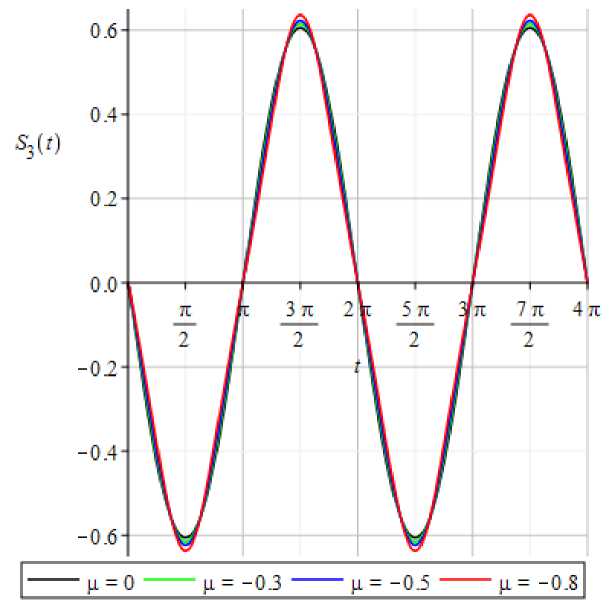
Рис. 3. Графики 2я- периодическому решению уравнения (7) в случае резонанса при ш2 = 1 и различных значениях параметра g.

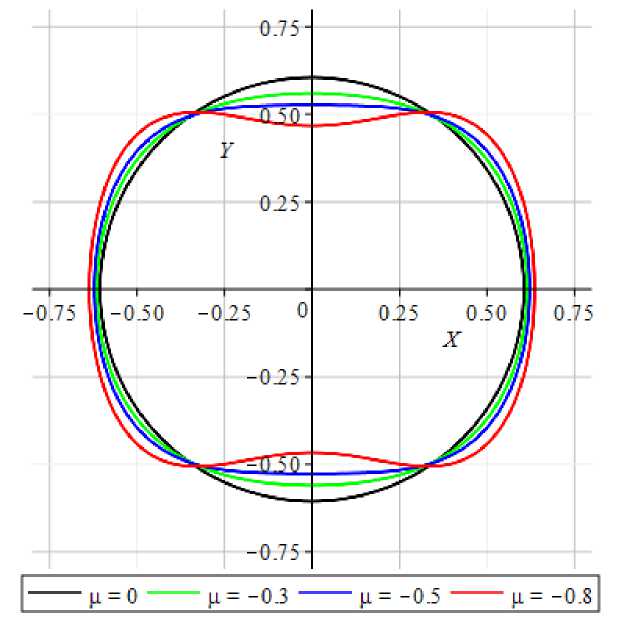
Рис. 4. Графики фазовых траекторий уравнения (7) в случае резонанса при со2 = 1 и при различных значениях параметра ц.

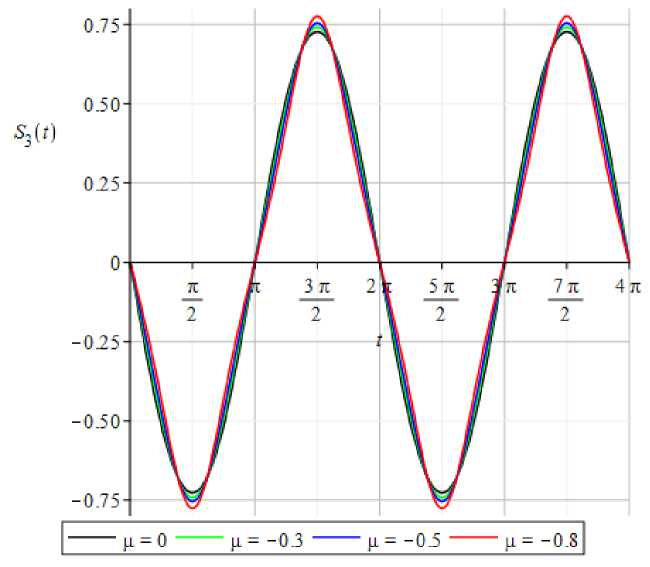
Рис. 5. Графики 2я- периодическому решению уравнения (7) вблизи резонанса при о² = 1 + ц и различных значениях параметра ц.

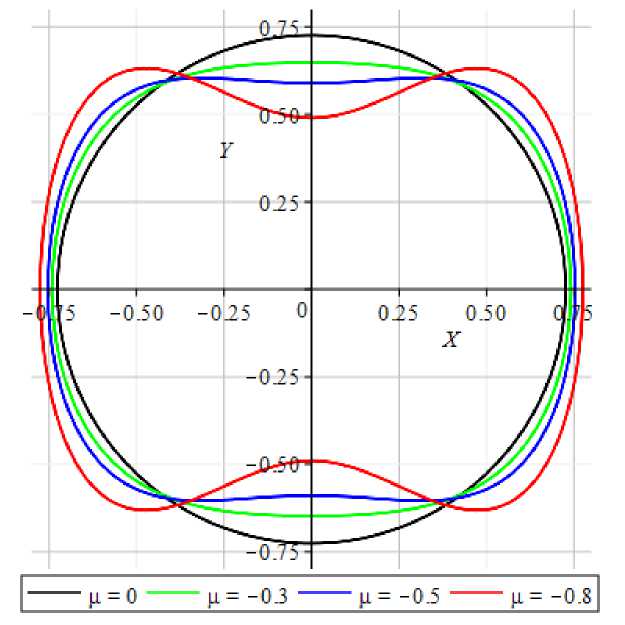
Рис. 6. Графики фазовых траекторий уравнения (7) вблизи резонанса при й)2 = 1 + . и при различных значениях параметра ..

Обсуждение полученных результатов. Достоверность результатов, полученных с помощью метода малых параметров, подтверждается сравнением их с численными решениями задачи Коши для соответствующих уравнений (1), (7) и (8). Начальные данные численных решений определялись из приближенных решений, полученных методом малого параметра.

Из графиков (рис. 1–6) видно, что случаи вдали резонанса и вблизи него имеют общую закономерность, заключающуюся в том, что при уменьшении параметра . по модулю 2n- периодические решения и фазовые траектории возмущенных уравнений приближаются к 2я-периодическим решениям и фазовым траекториям соответствующих невозмущенных уравнений. Причем вдали резонанса амплитуда колебания 2тт-периодических решений при положительных . больше, чем при отрицательных.

Вместе с тем есть и существенные различия. Если в случае вдали от резонанса фазовые траектории представляют собой непересекающееся семейство замкнутых кривых, то в случае резонанса каждая фазовая траектория возмущенной системы пересекает фазовую траекторию невозмущенной системы в четырех точках. Причем в случае резонанса (<д2 = 1, b = 0) эти четыре точки пересечения для всех фазовых траекторий возмущенной системы остаются неизменными, вблизи же резонанса (со2 = 1 + /л, b = 1, /л < 0) соответствующие точки пересечения для различных фазовых траекторий возмущенной системы несколько смещаются.