Вычисление радиационного давления на рассеиватель с произвольной амплитудой рассеяния при воздействии произвольного поля в идеальной жидкости

ВВЕДЕНИЕ. ПОСТАНОВКА ПРОБЛЕМЫ

Вопросам коагуляции различных частиц в ультразвуковом поле по-прежнему уделяется большое внимание. Актуальным в этом круге проблем является расчет радиационного давления на сложные конгломераты связанных между собой вследствие, например, процессов агглютинации, частиц. Ранее в работе [1] рассматривались выражения для сил радиационного давления на сложные конгломераты частиц в поле плоской бегущей и стоячей волн. В этом случае силы оказались зависимыми только от зональных гармоник в разложении амплитуды рассеяния препятствия по сферическим функциям. Поэтому не возникала необходимость рассмотрения общих выражений, связывающих силы радиационного давления со всеми коэффициентами в разложении амплитуды рассеяния препятствия по сферическим функциям. В настоящей работе полученные в [1] выражения обобщаются на произвольное падающее в идеальной жидкости поле и произвольную амплитуду рассеяния препятствия.

Пусть амплитуда рассеяния препятствия f ( 9 , ф ) известна. Необходимо по аналогии с работой [1] выразить компоненты силы радиационного давления через характеристики амплитуды рассеяния, но уже не в плоской волне, а произвольной по форме волне в идеальной жидкости.

РЕШЕНИЕ ЗАДАЧИ

Поле в волновой зоне рассеивателя (источника) имеет вид

ikr

Р ( r , 9ф ) = f ( 9 , ф ) — + O I — I . r V kr )

Здесь ( r , 9 , ф ) — сферические координаты точки наблюдения; p — полевая характеристика акустического поля, например давление; к — волновое число.

Согласно работе [2], всякая дважды непрерывно дифференцируемая по своим аргументам 9 , ф функция f ( 9 , ф ) может быть разложена в ряд Фурье по системе сферических функций Y l^m ( 9 , ф )

P l^m (cos 9 )cos т ф ,   m = 0,1,..., I ;

P m (cos 9 )sin| m| ф , m = - 1, - 2,...,- 1 ,

а именно

to f (9, ф) = ^

l = 0

A ⁰ P l (cos 9 ) +

+ ^ [ A l cos т ф + B l sin m y _ P, (cos 9 ) , ⁽³⁾ m = 1                                                        _

где коэффициенты определяются так:

'A,^m ] = 2 I + 1 ( I - m )! _x \ B = 2 n (1 + 5 o m )( 1 + m )! ^x

n 2n xJJ f (9, ф)P (cos 9)

0 0

cos m ф sin m ф

sin 9 d 9 d ф ,

P l^m — присоединенные полиномы Лежандра. Согласно, например, [3], амплитуда рассеяния удов-

летворяет условиям разложимости в ряд (2).

Известно [4], что вне рассеивателя совершенно идентичное поле (1) может быть создано системой мультиполей, сосредоточенных в одной точке внутри рассеивателя. Свяжем эту систему мультиполей с амплитудой рассеяния. Для этого будем почленно дифференцировать уравнение ikr

( А + к ²) — = - 9 ( х Ж y Ж z )

\       / 4nr

представляет собой ряд по степеням a _i углов cos 9 = sin 9 cos ф , cos 9 ₂ = sin 9 sin ф и cos 9 ₃ = cos 9 вида (7), то это отвечает соответствующему ряду мультипольных источников вида (6).

В работе [1] приведен мультипольный источник, создающий азимутально-симметричное поле с амплитудой рассеяния

с помощью оператора

д ^а 2 д ^а )

а

D a = ',     ,

(д х ^а ’ yy ^{a 2} д z

ю f (9) = £ At 0 p (cos 9),            (8)

I = 0

■ ^а 3

,

| а = а 1 + а ₂ + а ₃, a_i — натуральные числа.

Имеем:

и имеющий вид

5 f ( 9 ) = ^{4 П Х}

ikr

( А + к² ) D ^a ^| =

'       ²    ( 4 n r J

= - D ^a ( J ( х Ж y)5)) =

= - 9^{( а 1 )} ( х Ж ^и ) ( y ) 5 ^{И з} ) ( z ).                ⁽⁵⁾

Здесь - 9 ^й ( x ) = -S ^и ( х) 3^{( а 2} ) ( y ) 3 ^{И з} ) ( z ) — мульти

ю

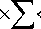
[ l ^/2 ]

A ° Z ( - 1) ⁿ

x 9 ( х ) 9 ( y ) 9 ( z ).

Внутренняя

поль порядка и , сосредоточенный в начале коор

(2 I - 2 n )!      Г1 D |* ^{2 2}

2 l n !( 1 - n )!( 1 - 2 n )l ( ik ^z J

сумма в (9) равна

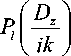
D_z =д / д z ; [ ^ ] означает взятие целой части чис

ла; P l — полиномы Лежандра. Попутно полезно

привести тождество

динат. В получившемся решении

D 1 ^а 1

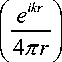
удерживаем только слагаемые с порядком O(r 1). Тогда, очевидно, дифференцировать нужно только числитель. Введем обозначение пИ (>• P (r ,е,ф)

4 n r

= ( ik ) ^И ( sin 9 cos ф ) ^а ( sin 9 sin ф ) ^и cos ^{a з} 9 4—.

Таким образом, мультиполь из (5) создает дальнее поле с амплитудой рассеяния fа (9, Ф) =

( ik )' ^а ( sin 9 cos ф ) ^а ( sin 9 sin ф )^{а 2} cos ^{a з} 9 4 п

,

а мультиполь

- 4 п Д- 9^(а ) ( х ) 9^(а 2 ) ( y Ж'" ) ( z ) ( ik ) ^а

соответствует амплитуде рассеяния

[ у _{( - 1)} n       (2 1 - 2 n )!       _s 1

n^o       2 ln!(1 - n)!(1 - 2 n)!    , следующее из свойства полиномов Лежандра P(1) = 1, I = 0,1,2,... и оказывающееся полезным при расчетах радиационного давления, например, в случае плоских первичных волн.

Получим выражение для мультипольного источника 5 f( _9ф ) , создающего поле с амплитудой рассеяния f ( 9 , ф ), из (3). Для этого, в частности, понадобится тождество [2]

m pm (х) = (1 - х2) m/2-mP1 (х),       (10)

или для х = cos 9

m pm (cos 9) = sinm 9---d----p (cos 9).   (10а)

(dcos 9 ) ^m ‘

Искомое выражение для мультипольного источника 5f (9 ф) получим, следуя технике разложения мультипольных полей (подчеркнем: полей, а не источников), изложенной в [5, 6]. Сначала применим к eikr дифференциальный оператор fи (9,ф) = (sin9cosф)а (sin9sinф)а2 cosaз 9. (7)

Таким образом, если амплитуда рассеяния

m

—D _x + iD_vA  e^ltr

:К\ х y)

= sin ^m 9 e '^{m ф} e '^kr =

= sin ^m O (cos ж ф + i sin т ф )e^licr ,         (11)

d где Dx = ^, Dy = dx

d d y

Основываясь на выражениях (3), (6), (7), (10), (11), можно записать окончательное выражение для мультипольного источника S f_{( 0ф} ) , обеспечи

сопряжение; ( x _1; x ₂, x ₃) = ( x , y , z ); p — плотность среды, го — круговая частота. В (14) в качестве p_s ( x ) следует использовать решение p ( x ) уравнения (13). С учетом этого, а также (12) выражение (14) перепишется в виде

вающего поле с амплитудой рассеяния f ( 0 , ф) из (3):

™

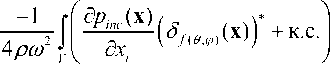
^S f ( 0ф ) = - 4 ^ ^

I = 0

A⁰ P I - D 1+ llz V ik J

п у. pro² 1 =0

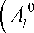
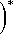
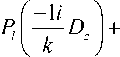
lm

m kl (Al" Re ( Dx + iDy) + m=1V ik 7 х L                J

m

+ У|--^ I [(Am) Re D + iDvT + l                 x y m =1 v k J '            L               J

*                   m^m

+ ( B m ) Im [ ( D . + ID , ) J ) d u m P l ( U )

+ B” Im ( D + iD l           у x         ^y

m d ^m

) ] )      P ⁽ u )

_x d p i„c (x)

X S ( x ) S ( y ) S ( z ).

d x i

+ к.с.

Так, в качестве примера дифоператор при A ₁ ¹

равен D , при B1 — D . Остальные компо-ik                    ik ненты в (12) также вычисляются тривиально. Из (12) в случае азимутальной симметрии непосредственно следует (9).

Таким образом, решением уравнения

Стоящий слева в (15) дифференциальный опе- ,             dp„_r ( x )

ратор воздействует на функцию inc , после dxi чего получившаяся функция рассматривается в точке x = 0 .

Соответствующая составляющая квадратичной компоненты равна [1]

( A + k ² ) p ( x ) = S f ( о , ф ) ( x )              (13)

___( _ss )            1 ^п 2 ^п

Fi   =- 2 p c ? J J| f ( 0 , ф )|²cos O sin о d ф d 0 . (16)

будет поле давления p ( x ) с асимптотикой (1), характеризующейся угловым распределением f ( 0 , ф ) из (3), где ^S f ( о , _ф ) ( x ) — мультипольный источник, определяемый выражением (12).

Полученное выражение (12) для общего случая амплитуды рассеяния и его частный случай азимутальной симметрии (9) могут быть использованы для вычисления радиационного давления на произвольном рассеивателе в произвольном же первичном поле [1, 7]. Так, i -я составляющая перекрестной компоненты радиационного давления определяется выражением [1]

Углы O i , i = 1,2,3 описаны выше, f ( 0 , ф ) определяется из (3).

Выражение (16) выразить в простой форме через коэффициенты A_l ^m и B_l ^m в отличие от случая азимутальной симметрии не удается, однако его вычисление тривиально.

⁽ is )        -I

^Fi = Й 2~

4 pro

x f pT ^(x) ( a + k ² ) P s * ( x ) + к.с. | d V .    (14)

V V ^d x i                            J

Здесь p_inc ( x ), p_s ( x ) — давления падающего и рассеянного полей; звездочка означает комплексное

ВЫВОДЫ

Таким образом, с помощью использования точечного мультипольного источника, создающего поле рассеяния, эквивалентное реальному, удалось получить компактные выражения для расчета сил радиационного давления в произвольном падающем поле.

Настоящая работа выполнена при поддержке фонда РФФИ, грант № 05-03-33108, и целевой научно-технической программы Российской Федерации "Исследования и разработки по приоритет-

ным направлениям развития научно-технологического комплекса России на 2007–2012 годы", лот 2, шифр "2007-2-2.2-04-08".