Вычисление собственных функций ограниченного дробного преобразования Фурье

Дробное преобразование Фурье (ДрПФ) – это семейство линейных преобразований, обобщающих преобразование Фурье. Обычная интерпретация преобразования Фурье – преобразование сигнала из временной области в его частотную область.

Каноническое ДрПФ рассмотрено [1] как Фурье– преобразование a -степени, где a - действительное число. Таким образом, происходит преобразование сигнала между временной и частотной областями. Можно рассматривать ДрПФ как операцию вращения частотновременного распределения на некоторый угол [2].

Изначально ДрПФ рассматривалось в приложениях для квантовой механики. Однако в последнее время оно привлекло повышенное внимание исследователей в оптике, в результате чего были выполнены обширные исследования по его свойствам, оптической реализации и потенциальных приложениях в оптике. Таким образом, в настоящее время ДрПФ активно используется при анализе в оптической обработке информации [3]. Кроме того, что дробное преобразование является удобным инструментом при описании различных явлений в оптике и квантовой механике, дробление некоторого преобразования даёт новую степень свободы (порядок дробления), которая может быть использована для более полного описания объекта/сигнала или как дополнительный кодирующий параметр.

ДрПФ используется в решении дифференциальных уравнений, в квантовой механике и квантовой оптике, в оптической теории дифракции, в описании оптических систем и оптической обработке сигналов, включая применение частотных фильтров, временной фильтрации и мультиплексировании, а также при распознавании образов, в вейвлет-преобразованиях, при операциях над чирп-функциями, при кодировании, создании нейронных сетей и др. Подробный обзор приложений можно найти в работе Т. Алиевой с соавторами [3].

Среди методов оптической реализации ДрПФ можно назвать модульную линзовую систему, систему из нескольких сферических и/или цилиндрических линз [4–8]. Некоторые из таких систем, особенно с цилиндрическими линзами, используются для астигматического преобразования с целью формирования вихревых пучков [5, 8– 10].

Одним из приложений ДрПФ является описание распространения лазерного излучения в средах с градиентным показателем преломления [11, 12].

В данной работе используется одномерное ДрПФ для моделирования распространения оптических сигналов в оптическом волноводе с параболической зависимостью показателя преломления. В случае бесконечной среды аналитическое решение для собственных функций среды известно [1] и описывается модами Эрмита–Гаусса (ЭГ). При учёте поперечной ограниченности градиентного волновода необходимо численно решать задачу на собственные значения и функции. В данной работе выполняется расчёт собственных функций при различных параметрах волновода с квадратичным показателем преломления.

Дробное преобразование Фурье

Рассмотрим одномерный случай прохождения светового пучка через градиентную среду с ограниченной входной областью (рис. 1). Дифракционные эффекты, связанные с данными пространственными ограничениями, влияют на результат прохождения.

------*"    ! d

_____JL

Среда с градиентным показателем преломления

Рис. 1. Схема оптической системы

Параксиальное распространение входного пучка через ABCD-систему может быть описано следующим образом [13]:

F ( и ) =

—^

exp 2ikB ( Ax ^{2 —2} xu ⁺ Du ²) d x,   ⁽¹⁾

где f ( x ) – поле на входе оптической системы, F ( u ) – результат на выходе, n ( x ) = n 0 (1 - ( x 2 /2 a 2 )) k = 2 п / % -волновое число, A , B , C , D – параметры системы.

В случае градиентной среды коэффициенты определяются как [14, 15]:

задача является задачей нахождения собственных функций оператора распространения:

L [ fn ]=Ц nfn ,

A B cos ( z / a ) a sin ( z / a ) C D     - sin ( z / a ) / a cos ( z / a )

где z – дальность распространения, a – параметр, связанный с функцией изменения показателя преломления среды.

Тогда формула (1) может быть переписана как ДрПФ:

Г а [ f ( X ) ] = F a ( U ) Ц

k

2 п ia sin a

+^

J f ^{( x} )

-^

X

exp

ik

2 a sin a

(

x ² cos a- 2 xu + u ² cos a

) d x ^,

где a = z / a .

Если принять во внимание, что на входе система является ограниченной, как показано на рис. 1, то тогда из соотношения (3) для неё получается ограниченное ДрПФ:

r a , d [ f ( x ) ] = F a , d ( U ) =

k

2 п ia sin a

d /2

J f ( x )

- d /2

X

X exp

ik

2 a sin a

(

x² cos a- 2 xu + u² cos a

) d x ,

где d – ширина ограниченной области.

Распространение световых пучков через заданную градиентную среду обладает свойством периодичности, которое справедливо как для неограниченного преобразования, так и для ограниченного. Период самовоспроизведения составляет z T = 2 п a . При этом на расстоянии z_{T /4} = п a /2 ДрПФ вырождается в обычное преобразование Фурье, справедливое для линзовых систем. В плоскости z_{T /2} = п a исходное изображение «переворачивается», а в плоскости z 3 T _/4 = 3 п a / 2 полученный результат эквивалентен применению обратного преобразования Фурье для исходной функции.

Обозначим оператор, соответствующий преобразованию (3), через Г α . Для ДрПФ характерны свойства коммутативности и аддитивности:

Va , в : r a₊e =r a F e =r e F a . (5)

Отметим, что свойство коммутативности не работает в общем случае для произвольной параксиальной ABCD-системы, отвечающей уравнению (1), и для ограниченного преобразования (4).

Поставим нашей целью отыскать такой класс функций, которые самовоспроизводятся на произвольном расстоянии, не обязательно кратном z T . Иными словами, требуется найти набор функций { h_n } , инвариантных к прохождению через оператор Г α . В общем случае такая

где L – произвольный линейный оператор, µ n – собственное значение, отвечающее собственной функции f n .

Решения поставленной задачи для неограниченного оператора (3) хорошо известны – они представляют собой моды ЭГ [16]:

h n ⁽ x ) = exP

x ²

2 o ₀ ²

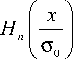
Моды ЭГ проходят через оператор распространения Г α , не изменяя своего вида (с точностью до фазового набега), каким бы ни был параметр α.

Ограниченное дробное преобразование Фурье

Существенный интерес представляет задача нахождения распределений, которые самовоспроизво-дятся в условиях ограничения входной области, т.е. собственных к оператору распространения Г α, d (4).

Если на вход подать собственную функцию такого оператора, то на расстоянии z = a a данная функция будет самовоспроизводиться в промежутке [ - d /2, d / 2]. Желательно, чтобы полученные собст-

венные функции не зависели от параметра a (пройденного расстояния), как и в случае с модами ЭГ. Это

дало бы возможность использовать их для передачи информации без искажений в системах, ограниченных не только на входе, но и на всей области распространения. Схема такой оптической системы изображена на рис. 2.

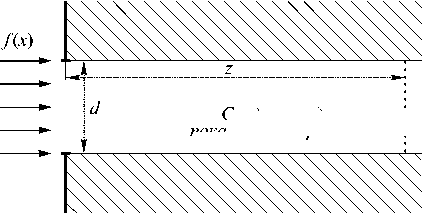
Рис. 2. Оптическая система с ограничением всей области распространения

Среда с градиентным показателем преломления

Поставленное условие соответствует тому, что множества функций во входной и выходной плоскостях, определённых на заданном промежутке, совпадают. Таким образом, можно задать скалярное произведение, зависящее от d :

d /2

( f ^, g ) = J f ^{( x} ) g * ^{( x )d x} .                          ⁽⁸⁾

- d /2

Введённое скалярное произведение позволяет рас

* смотреть сопряжённый оператор F a , d :

(ra,d [ f ], g) = ( f, ra,d [g]) .                           (9)

Используя теорию линейных операторов, можно определить вид сопряжённого оператора:

^. d [ f ( и ) ] =

ik

2 п a sin а

d /2

J f ( и )

- d /2

X

x exp

—ik

2 a sin а

(

и ² cos а— 2 xu + x ² cos а

) d u .

Тогда будет существовать набор ортогональных функций { ф _n ( x ; а , d )}, удовлетворяющих уравнению на собственные значения:

г а , d ^[Га , d [ ф n ] ] = g |² ф n

а также аналогичный набор { х _n ( и ; а , d )} для уравнения:

^Га , d [ ^га , d [ X n ] ] = | g n |² X n ,

причём эти функции связаны между собой следующими соотношениями [17]:

^Га , d [ ф n ] = g n X n ,                                    ⁽¹³⁾

^Га , d [ X n ] = g n ф n ■                                    ⁽¹⁴⁾

Отметим, что в общем случае оба набора функций не являются собственными для исходного оператора.

Оператор Г ^ _d Г _а , _d может быть записан как:

d /2     Го,              1

^га , d ^[га , d [ f ⁽ x ) ] ] = J exp i y-( u ^{2 —} x ²)ctg4^x

— d /2      I ² a

■ (   kd, sin I

I 2 a sin а x--------- п( и — x)

—

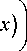
f ( x )d x .

В частности, если а = п / 2 , мы получаем: Г П /2 Л [Г п /2, d [ f ( x ) ] ] =

^d / ² sin ( kd ( и — x ) /2 a )                           ⁽¹⁶⁾

= J ------- V( x )d x .

— d /2        ^п ( ^{и — x} )

Соотношение (16) хорошо известно в теории сфероидальных волновых функций (СВФ), которые являются инвариантными относительного преобразования Фурье на ограниченном промежутке [18]. Таким образом, собственные функции ф _n ( x ; п /2, d ) рассматри

Особенности расчёта СВФ через приближение конечными рядами и матричным методом были рассмотрены в работах [19-22].

Отметим, что функции ф _n ( x ; а , d ) обладают свойством самовоспроизведения на расстоянии z = o a с точностью до изменения фазы (амплитуда сохраняется).

Преобразование, основанное на инвариантности к сфероидальным волновым функциям

В работе [1] рассматривается вывод дробного преобразования Фурье через инвариантность к модам ЭГ. На основании этого можно попытаться вывести аналогичное ограниченное преобразование через СВФ.

Рассмотрим некоторое преобразование Ф _а , которое бы изменяло вид СВФ ф _n ( x ), добавляя фазовый набег:

^Фа [ ф n ⁽ x ) ] = exp ( i ^а n ) ф n ⁽ x ). ⁽²⁰⁾

Для а n = п n /2 данное преобразование вырождается в последовательное применение операций преобразования Фурье, если n <  N , где N - число степеней свободы системы, определяемое размерами области определения и ширины спектра СВФ [23]. Если же брать СВФ с индексом больше, чем N , то соответствующие им собственные числа по модулю будут близки к нулю, что приведёт к нарушению равенства (20).

СВФ образуют ортогональный базис функций, заданных на ограниченном интервале [ — d / 2, d / 2] . Это означает, что по данному базису можно раскладывать произвольные функции, заданные на этом же промежутке [24-26]. Будем рассматривать только такие функции, которые можно разложить по первым N СВФ:

N f (x ) = S cn ф n(x), (21) n=0

ваемого оператора являются СВФ ф _n ( x ; п /2, d ).

Учитывая упомянутое выше свойство инвариантности сфероидальных функций, а также вид ДрПФ, нетрудно показать, чему равняются функции { ф _n ( x ; а , d )} и { х _n ( и ; а , d )}:

где c_n - коэффициенты разложения. Будем считать, что СВФ нормированы. Тогда коэффициенты можно найти следующим образом:

C n = d J ² f ( и ) ф П ( и )d и ,                          (22)

— d /2

ф _n ( x ; а , d ) = ф _n ( x ; а , d ) exp { — ikx ² ctg а / 2 a } , (17)

X _n ( и ; а , d ) = ф _n ( и ; а , d ) exp { iku ² ctg а /2 a } ,    (18)

где СВФ ф _n ( x ; а , d ) могут быть численно найдены из соотношения:

d .² sin ( kd ( и — x ) /2 a sin а )

— ------------------ ф n ( x ; а, d ) dx =

— d /2          ^п ( ^{и — x} )                                  (19)

= | g n ( а , d )|² ф n ( и ; а , d ).

где звёздочкой обозначено комплексное сопряжение. Стоит отметить, что СВФ являются действительными, поэтому этот знак можно опустить.

Применим преобразование Ф ^ к функции f ( x ):

N

^Фа [ ^{f (} x ) ] = S ^Cn ^Фа [ ф n ⁽ x ) ] =

N          n = ^o                                       (23)

= S ^cn ^ex p ( i ^а n ) ф n ⁽ x ).

n = 0

Подставим в (23) коэффициенты C_n из (22):

Фа[ f ( x )] = d/2 [ Л                      1                (24)

= J S exp ( i а n ) ф n ( x ) ф „ ( и ) f ( и )d и .

— d /2 L n = ⁰                                _

Формула (24) осуществляет преобразование, относительно которого СВФ (с номерами меньше N ) и их суперпозиции сохраняют свой вид во время распространения. Ядром преобразования в данном случае является внутренняя сумма:

N

к ( x , u ) = £ exp ( i a „ ) у n ( x ) y ( u ). (25) n = 0

Можно увеличить число слагаемых в сумме до бесконечности, превратив её в ряд, можно также подставить в преобразование произвольную функцию, однако это не избавит от двух основных проблем.

Во-первых, ядро преобразования содержит сумму (либо ряд в случае N →∞), вычисление которой сложно осуществлять. Во-вторых, не ясно, какой оптической среде соответствует такой оператор . Тем не менее, наличие этой формулы даёт направление исследований для построения оптической системы, где бы энергия ни выходила за заданные границы области распространения.

Результаты моделирования

Численный расчёт выполнялся при следующих параметрах: длина волны 1 = 1 мкм, квадратичная функция изменения показателем преломления среды задана параметром a = 25 1 , ширина волновода выбиралась различная. Соотношение a = z / а будет меняться в пределах от 0 до 2 п . Далее картина периодически повторяется.

Сначала зададим ширину входной области d = 24 1 и рассчитаем собственные функции для параметра a = п / 5. График модулей первых собственных значений в этом случае принимает вид в соответствии с рис. 3.

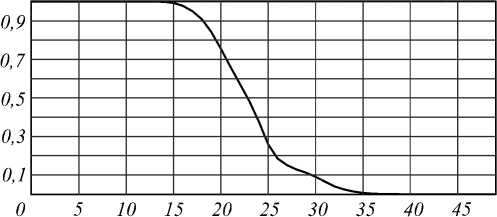
Рис. 3. Модули собственных значений при а = п /5,d = 24 1

График имеет «ступенчатый» вид, поэтому можно сделать вывод о том, что только первые собственные функции, у которых собственное значение не равно нулю, распространяются в заданной среде без потери энергии. Первые три собственные функции изображены на рис. 4.

Как видно из рис. 4, собственные функции очень напоминают моды ЭГ. Распространение 4-й моды показано на рис. 5. Вид функции не меняется с точностью до фазового набега.

Вычислим теперь функции из соотношений (17) и (18). Стоит отметить, что расчёт СВФ, присутствующих в данных формулах, характеризуется неустойчивостью и зависит от ширины волновода d . Полученные функции были рассчитаны при параметрах d = 20 1 , a = n /3.

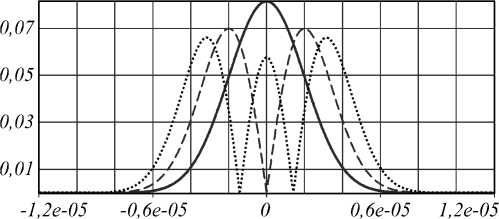
Рис. 4. Амплитуды собственных функций при а = п /5,d = 24 1

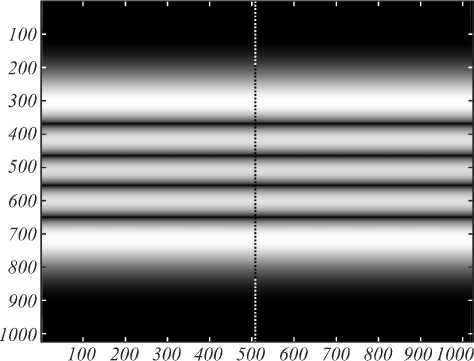
Рис. 5. Распространение четвёртой собственной функции, рассчитанной при а = п /5,d = 24 1

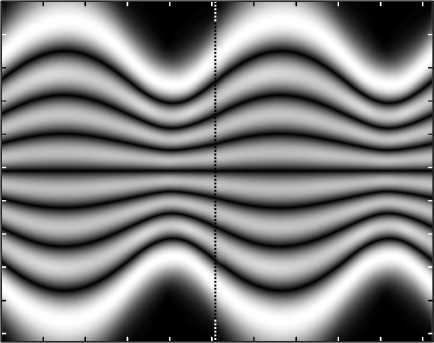
Результаты распространения рассчитанных функций ф ₇( x ; a , d ) и / 7 ( x ; a , d ) показаны на рис. 6 а , 6 б соответственно. Как видно из рисунков, данные функции действительно восстанавливают свой вид на расстояниях z = а п /3 и z = 2 а п /3 соответственно.

Уменьшим размеры входной области до d = 12λ и посмотрим, как меняются соответствующие результаты. На рис. 7 представлен график полученных собственных значений. Как видно, количество ненулевых значений сильно сократилось по сравнению с предыдущими расчётами. Это говорит о том, что число степеней свободы системы уменьшилось.

Собственные функции, изображённые на рис. 8, тоже изменились: на краях области определения они перестали обращаться в ноль.

На рис. 9 показано моделирование распространения собственной функции с номером 4. По сравнению с рис. 5 вид изображения сильно изменился. Данная функция имеет собственное число, меньшее единицы, а значит, распространяется в волноводе с потерей энергии, т.е. не является модой волновода.

Заметим, что расчёт функций, собственные значения которых меньше единицы, затруднён, т.к. задача на собственные значения становится неустойчивой. Проблемы неустойчивого расчёта в описанных условиях отмечались также при вычислении СВФ конечными рядами [19, 20].

Таким образом, набор функций, имеющих собственные значения, близкие к единице, однозначно определяет число степеней свободы рассматриваемой оптической среды и возможность передачи оптического сигнала без искажений.

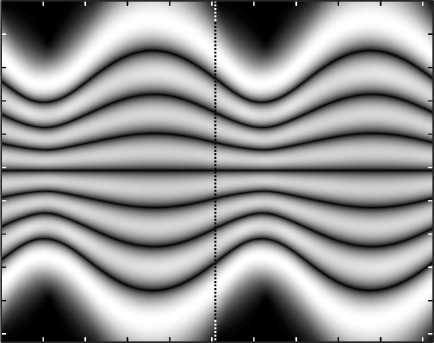
• a)    100 200 300 400 500 600 700 800 9001000

• б)       100 200 300 400 500 600 700 800 9001000

Рис. 6. Распространение функций ϕ ₇ (x; α ,d) (а)

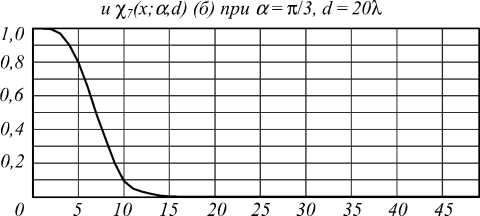
Рис. 7. Модули собственных значений при α = π /5, d = 12 λ

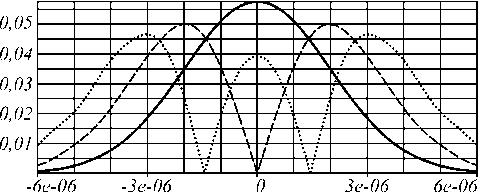
Рис. 8. Амплитуды собственных функций при α = π /5, d = 12 λ

Заключение

В работе рассмотрено одномерное ДрПФ, соответствующее градиентным оптическим средам.

Рассмотрен пространственно-ограниченный оператор распространения в градиентной среде на основе ДрПФ. Выполнен расчёт собственных функций при различных параметрах оптического волновода с квадратичным показателем преломления.

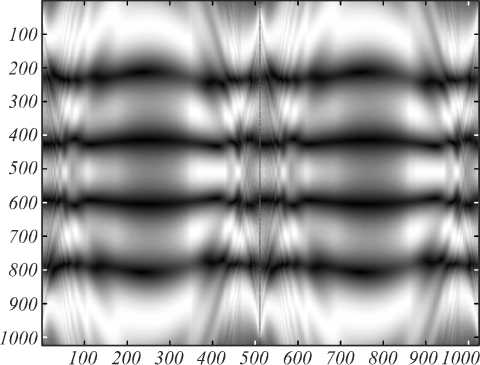
Рис. 9. Распространение собственной функции, рассчитанной при α = π /5, d = 12 λ

Также рассмотрены «парные» собственные функции, соответствующие «входу» и «выходу» из оператора распространения.

Результаты численного моделирования показали, что функции, собственные значения которых близки к единице, практически полностью входят в ограниченные размеры волновода и похожи на моды Эрмита– Гаусса, а также сфероидальные волновые функции.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ, а также Российского фонда фундаментальных исследований (грант 14-01-31401 мол_а).