Вычисление средней температуры n-слойной стенки

В работе [1] при построении математической модели теплового режима здания (ТРЗ) полагалось, что средняя температура его наружной стены в квазистационарном приближении может быть вычислена по формуле t = ^,                          (1)

где t _B - температура внутреннего воздуха, t_н - температура наружного воздуха.

Однако данное допущение предполагает, что выполняются следующие условия:

• 1) коэффициенты теплоотдачи для внутренней и внешней поверхностей стенки а_в, а н ^ да [2];

• 2) стенка однослойная.

В реальных условиях а_в и а н имеют конечные значения, кроме того, наружные стены, как правило, многослойные. Поэтому возникает задача уточнения формулы для средней температуры наружной стены здания. Для решения этой задачи рассмотрим процесс теплопроводности в n-слойной ограждающей конструкции. Для иллюстрации последующих выкладок на рис. 1 приведена схема двухслойной стенки.

Здесь и далее через 5 ^ обозначим толщину всей стенки, имеющей в общем случае n слоев (в случае рис. 1 слоев 2), а через 6 i - толщину i- го слоя, t_Bn - температура внутренней поверхности стены, t_Hn - температура наружной поверхности стены, t (_l_₁)__l - температура на границе ( i- 1) - го и i- го слоев, t - средняя температура i- го слоя, R ^ - термическое сопротивление теплопроводности всей стенки, а R _t - ее i- го слоя.

Нетрудно показать, что температуры на внутренних границах слоев будут равны:

tl_2=tRO -(tBn — ^)-§;(2)

• t2_3 = tBn — (tBn — tHn) • \ 2 ;

Re

• t3_4 = tBn — (tBn — tHn) • 1 o2  ~;

^t (n_l)_n ^t Bn ^(t Bn    ^t Hn ) ^X

X R i +R+R + ^+R n-i

Re.

Обобщая полученные соотношения,

(5) запишем,

что

• ti_(i+i) = tBn — (tBn — tHn) • ^kR1 k .

R e

При этом следует иметь в виду, что температура наружной поверхности формально может быть представлена следующим выражением:

• ^t Hn = ^t Bn - ^(t Bn - ^t Hn ) • ^^k_R^{1 k}-             ⁽⁷⁾

Re

Так как температура по толщине каждого слоя распределяется по прямой, то его средняя температура будет равна полусумме температур на его границах, поэтому

• t i = ^t Bn ^{- (t} Bn ^- ^n ) •    ;                 ⁽⁸⁾

2R e

• ^f 2 = t Bn - ^(t Bn - t Hn ) • _2R^{2 ;               (9)}

2R e

• ^t n = ^t Bn ^{— (t} Bn ^{— t} Hn ) ^

_x 2R i + 2R 2 +2R ₃ +...+2R n-2 +R n-1

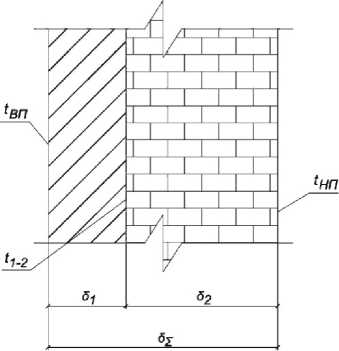
Рис. 1. Двухслойная стенка

Краткие сообщения

Следовательно, общая формула для средней температуры i -го слоя будет такой:

tl = t RO - (t RO — t_m) • ^^i .      (11)

2K £

Вычисляя среднюю температуру n -слойной стенки по известной формуле

• t ^_ T" • (t i • 5 i + t ₂ • S ₂ +... +t _n • S ^ ),      ⁽¹²⁾

OX получим следующее выражение:

t _ £   - ^(£ BO~ ^£ KO )

• x у / 6 . ry y i

  X

  R k + R i )

  
  
  
  

Таким образом, найдена формула, позволяю- щая вычислять среднюю температуру n-слойной стенки по температурам ее внутренней и внешней поверхностей, а также по толщинам ее слоев и их термическим сопротивлениям теплопроводности.

Выясним, как отличаются значения средней температуры многослойной ограждающей конструкции, вычисленные по разным формулам. В качестве примера рассмотрим двухслойную стенку, состоящую из керамзитобетона (6 _i =300 мм, R 1 = = 0,46 м ² -°С/Вт) и минеральной ваты (6 ₂ =100 мм, R 2 = 1,78 м ² ∙ °С/Вт). Примем наружную температуру равной t_н = –34 °С, а внутреннюю – t _в = 21 °С. m                                      -   2i+(~34)

Тогда по формуле (1) получим, что t _---2---=

= –6,5 °С. Заметим, что использование формулы (1) предполагает, что коэффициенты теплоотдачи для внутренней и внешней поверхности а в, ан ^ да, но при практических расчетах их значениях принимаются согласно [3]: ав = 8,7 Вт/ (м2 °С), а ан _ 23 Вт/ (м2 °С). С учетом этого, определены температуры внешней и внутренней поверхности стенки: tRO = 18,37 °С, а tHO = -33 °С. Тогда, условно полагая, что стенка однородная, получим, что t _ i^i^Z^-^^) _ -7,315 °С. Если же вычисле- ния проведем по формуле (13), то получим, что t_ 6,67 °С.

Выводы

Получена формула, позволяющая вычислять среднюю температуру многослойной плоской стенки в соответствии с физикой процесса переноса теплоты. Показано, что погрешности использования ранее предложенных в литературе формул достаточно существенные.