Вычислительная эффективность для решения задачи оптимизации оболочек вращения при ограничениях на флаттер

Рассматриваемая в статье задача относится к классу задач анализа и оптимизации панелей (пластин и оболочек) с точки зрения устойчивости к флаттеру. В настоящее время известны два типа панельного флаттера: первый -связанный, возникающий при взаимодействии двух собственных мод панели; второй - одномодовый, высокочастотный [1; 6]. В данной работе рассматривается первый тип флаттера при высоких сверхзвуковых скоростях с использованием поршневой (квази-статической) аэродинамической теории.

Для получения флаттерных характеристик в качестве базовой используется конечноэлементная модель, что дает возможность рассматривать геометрию оболочки в наиболее общем виде. Однако обращение к процедуре анализа состояния объекта оптимизации (прямой расчет) в оптимизационных алгоритмах реализуется многократно и связан со значительными вычислительными затратами. Одним из подходов, обеспечивающих их снижение является подход, основанный на поэтапной замене исходной «точной» модели упрощенной метамоделью.

В теории оптимизации указанный подход хорошо известен, и при его реализации, как правило, рассматривают аппроксимации трех видов: локальную, глобальную и промежуточную [8; 10] (последняя в англоязычной литературе именуется как mid-range ).

Целью данной работы является исследование вычислительной эффективности решения задачи указанно- 64

го типа с использованием локальных и промежуточных аппроксимаций.

1.    Конечноэлементная модель оболочки

Осесимметричная оболочка рассматривается как подконструкция составной тонкостенной конструкции вращения. При этом формируется ее параметрическая модель, описываемая Безье-функциями и определяемая координатами ключевых точек в двух подпространствах. В двумерном подпространстве, совпадающем с плоскостью осевого сечения оболочки, определяется меридиан, а в одномерном - распределение толщины вдоль меридиана (рис. 1).

Ng -1

x ⁽ t b ) = Х ф n„ X t b ) X i , ^g ,* i =0

Ng —1

У(tb) = X ФNg,i(tb)y, i =0

Ng —1

h (tb) = Хф Nt/( tb) hj, j=0

^ф Ng , i ( t b ) = C Ng t b (1 - t b )     ,       ⁽¹⁾

• ( i )    = N g !

^g   i !( N g — 1)!,

Ф N_t , j ⁽ t b ) = C N_t t b (1 - t b )     ,

( j ) =

C N t =

N t !

j !( N t — 1)

!,0 <  t b <  1.

В этих формулах x ( t b ), y ( t b ), h ( t b ) ,-искомые функции, x_i и y_i – координаты ключевых точек сплайна;

i = 0, Ng -1, где N - количество ключевых точек, задающих образующую оболочки; hj – координаты ключевых точек на числовой оси; j = 0, Nt -1, где Nt – количество ключевых точек, задающих распределение толщины вдоль образующей. На рис. 1 показан вариант оболочки при некотором фиксированном наборе значений координат всех ключевых точек. В качестве конечного элемента используется тонкостенный усеченный конус [4]. На основе принципа Гамильтона получаем уравнение колебаний консервативной системы как ансамбля конечных элементов:

( K - _ю ² M ) U a = 0 , (2)

где K - матрица жесткости; M -матрица масс; u_A - вектор амплитуд перемещений для узловых точек; ω – частота собственных колебаний.

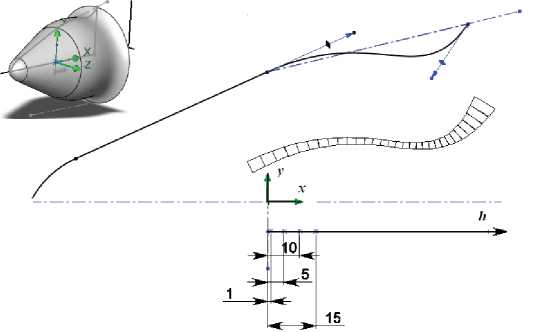
Р и с. 1. Геометрическая модель оболочки

F i g. 1. Geometric model of shell

Aэродинамическое давление определяется в соответствии с известным выражением [2]:

2 q   d w 1 M2 - 2 5 w pa = Mv-M(5s+Um 2 -1 s7

p U где q = a-2^— - динамическое давление потока; ρa – плотность газа; U – скорость потока; M – число Маха. В этом случае уравнение колебаний оболочки как неконсервативной системы приобретает следующий вид [3; 5]:

( K + p M + p p D + p A ) U a = 0 , (4)

гдеAиD–матрицыансамбляконечных элементов (аэродинамической жесткости и аэродинамического демпфирования соответственно); p – комплексная собственная частота. Если собственные вектора задачи (2) используются в качестве нового базиса, то уравнение флаттера приобретает следующую форму:

Gu + p p Du + p Eu = 0 , (5)

где G = Q + p A; Q - диагональная матрица, содержащая собственные значения, т. е. квадраты частот, соответствующих колебаниям в вакууме ω12,ω22,ω32 , и т. д. на главной диаго- нали; A=RTAR , D=R TDR ; u - собственный вектор в новом базисе; E -единичная матрица.

Дальнейшее решение сводится к анализу изменения комплексных собственных частот p при возрастании параметра потока. В качестве критерия наступления флаттера рассматривается появление в спектре кратных собственных значений с последующим выходом одного из них на положительную полуплоскость, что и соответствует колебаниям с возрастающей амплитудой, т. е. флаттеру. Детали построения и тестирования данной конечноэлементной модели подробно изложены в работе [4].

2.    Постановка и решение оптимизационной задачи

Оптимизационная задача ставится и решается как задача нелинейного математического программирования (НМП) в следующем виде:

найти min C (x) при ограничениях

A i ^ X i ^ B i ,i = 1, n, ф _к (x) ^ 0, k = 1, m , (6)

где x – вектор управляемых параметров; C ( x ) – целевая функция, выражающая собой критерий качества объекта проектирования (массу оболочки); n – количество управляемых параметров и, соответственно, количество геометрических ограничений (размерность пространства оптимизации); Ai и Bi , – геометрические ограничения снизу и сверху на управляемые параметры соответственно; m – количество функциональных ограничений. В качестве управляемых параметров рассматриваются координаты ключевых точек Безье (1).

При этом оптимизационная задача (6) решается с использованием аппроксимаций как последовательность оптимизационных задач с поэтапной заменой функций оптимизации упро- щенными аналитическими моделями (метамоделями), сформированными на основе анализа результатов экспериментов с исходной конечноэлементной моделью.

Промежуточные аппроксимации

В этом случае метамодели строятся поэтапно в отдельных подобластях пространства оптимизации конечных размеров, определенных движущимися границами на каждом этапе итерационного процесса. Таким образом, вместо исходной оптимизационной задачи (6) имеем серию оптимизационных задач следующего вида:

найти min C ⁽ r )(x) при ограничениях x ∈ Rⁿ

5 ⁽ r ) <  _r ⁽ r ) <  B ⁽ r )

- (\ i     i—       , (7)

i = 1,n,фкr)(x) > 0,k = 1,m,r = 1,N где C(r)(x) - аппроксимация целевой функции; фкr) (x) - аппроксимации функциональных ограничений; A/r) и Д.(r) - геометрические ограничения снизу и сверху соответственно; индекс r соответствует номеру этапа оптимизационного процесса; N – количество этапов, необходимое для достижения заданной точности.

Структура метамоделей такова, что включают в себя свободные параметры a i , i = 0 ,n , определяемые по результатам экспериментов, проведенных с конечноэлементной моделью объекта в P точках, назначенных в пространстве Rⁿ согласно некоторому плану эксперимента. Для определения свободных параметров используется метод взвешенных наименьших квадратов [8; 10], а в качестве аппроксимирующих функций – мультипликативная модель следующего вида:

C 5 (a) = a ₀17 ^ a ' a . (8)

l = 1

Локальная аппроксимация

В качестве метода, предусматривающего локальные аппроксимации, в данной работе используется метод Пауэлла [9] как последовательность задач квадратичного программирования:

min1d THd + V C (xjT d deRn 2       r при ограничениях

V ф _к (x r ) T d + ф _к (x r ) >  0, k = 1, m .

Матрица H _r представляет собой положительно определенную аппроксимацию Гессиана функции Лагранжа L (x, 2 ) = C (x) - 2 T ^ (x) , ^ (x) = ( ^ф 1 (х), ^ф ₂ (х),...., ^ф т (x)) T , r - номер итерации. При этом положительная определенность матрицы H _r обеспечивается итерационной BFGS-процедурой, использующей только градиенты функций и не требующей явного вычисления вторых производных. Компоненты вектора множителей Лагранжа X , соответствующие неактивным ограничениям, автоматически обращаются в нуль. Существенной особенностью метода является также то, что задача минимизации (1) формулируется в терминах шага d из некоторой исходной точки в направлении к оптимальной. Таким образом, x _{r + 1} = x _r + a _r d _r . Параметр a _r определяется как результат минимизации одномерной функции, исходя из предложенного Пауэллом критерия оптимального выигрыша по следующей схеме:

найти min © ( a ) , где

i =1

P = max

(I X^ p * +| 2 j),

где μ_i^* –

значение параметра μi на предыдущей итерации (на первой итерации ц = |2i|). Самой важной причиной для выбора нами этого алгоритма оптимизации являлся тот факт, что он относится к классу квазиньютоновских методов и требует для своей реализации только первые производные функций, т. е. анализ чувствительности первого порядка.

3.    Анализ чувствительности

Функциональные ограничения

Ф к^r ) (x) задачи (1) формулируются

_Р ⁽ k )

в виде Фкr)(x) = -^- -1, где р(k) - плот-Ро ность потока, соответствующая наступлению флаттера с формой колебаний, соответствующей волновому числу k = ng, ng = n1, n2 (n1 и n2 - начальное и конечное значение волнового числа в спектре учитываемых собственных значений задачи (4)) – минимальная плотность флаттера, соответствующая исходному проектному решению. Таким образом, в части анализа чувствительности актуальной является задача определения частных производных х 1 др (kk    R

ф;r '(x). =—:--— . В соответствии k     '' р ™n дxi с работой [3] производные от плотности должны определяться следующим образом:

ef = Re[(v TT xu)/(v TT p u)] (10) dXi Re[(vTT^, u)/(vTTpu)], 1 ’ где матрица T = Q+ p A + G + 2

+ PPDD + P E, T, Xi,T, Pi,T, Pai" частные производные от x(tb) по xi, p и pa соответственно; v - собственные вектора сопряженной по отношению к (5) задачи. В работе [12] представлены детали численной реализации формулы (10) и результаты в отношении анализа чувствительности к флаттеру оболочек различного вида.

4.    Программная реализация

Высокий уровень развития программных средств в виде CAE-систем делает бессмысленной разработку программного обеспечения «с нуля», при этом проблема расширение функционала этих систем является достаточно актуальной. Одним из примеров решения задач рассматриваемого класса на подобной основе может служить, в частности, подход, представленный в работе [7]. В данной работе программная реализация представляет собой два dll-модуля, являющиеся AddIn-приложениями к системе SolidWorks и в полной мере использующими функционал SolidWorks на основе API и COM-интерфейсов [4–5]. В частности, SolidWorks используется в качестве пост- и препроцессорного средства; кроме этого, используется функционал SolidWorks Flow Simulation для решения аэродинамической задачи. В остальном изложенные в данной работе методы и алгоритмы расширяют штатный функционал SolidWorks.

5.    Результаты и выводы

В работе [11] представлены результаты решения задачи оптимизации по массе оболочки вращения, геометрия которой и распределение толщины заданы согласно (1), N _g = 2 , N _t = 2 , а в качестве метода решения частных задач (7) использовался метод Бокса (нулевого порядка), будем условно этот подход идентифицировать символом A. В данной работе указанная задача была решена двумя методами: 1) на основе многоточечных промежуточных аппроксимаций и с использованием метода Хана и Пауэлла для решения задач (7); 2) на основе локальных аппроксимаций в виде (11), т. е. метод Хана и Пауэлла был использован напрямую без построения промежуточных метамоделей (10). Будем идентифицировать два последних подхода как B и С соответственно. Результаты решения задачи A, B и С полностью совпали, при этом с точки зрения вычислительной эффективности походы A и B друг от друга практически не отличаются, поскольку анализ метамоделей (8) не требует значительных вычислительных затрат.

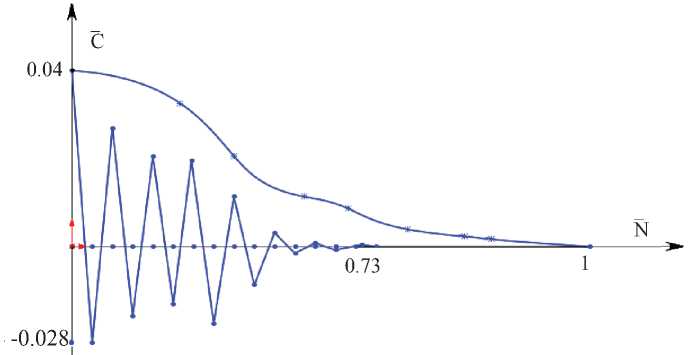
Р и с. 2. Aнализ вычислительной эффективности

F i g. 2. Analysis of computational efficiency

Одним из важных критериев вычислительной эффективности оптимизационного алгоритма является количество обращений к процедуре прямого расчета. Поэтому сравнение вычислительной эффективности подходов B и С представлен на рис. 2 в следующих безразмерных координатах: по о с и абсцисс откладывается параметр N = N ₀ / N _{A max} , где N ₀ – количество совершенных обращений к процедуре прямого расчета; N _{A max} – общее количество обращений к процедуре прямо

• - C - C o_M го расчета в подходе B, C =---- —,

^Copt где С – значение целевой функции при N ₀-ном обращении; C _opt – оптимальное значение целевой функции.

В заключение отметим, что метод промежуточных аппроксимаций обеспечивает значительное снижение вычислительных затрат (до 30 %) по сравнению с аппроксимациями локального типа. При этом выбор метода решения частной оптимизационной задачи с точки зрения трудоемкости не имеет существенного значения.

Практический опыт работы, полученный в процессе решения оптимизационных задач разного рода, позволяет также утверждать, что метод промежуточных аппроксимаций наиболее эффективен на начальных стадиях оптимизации в режиме интерактивного вариантного проектирования.

СПÈСÎÊ ÈСПÎËЬЗÎВÀÍÍЫХ ÈСТÎЧÍÈÊÎВ

• 1.    Алгазин, С. Д. Флаттер пластин и оболочек / С. Д. Aлгазин, И. A. Кийко. – Москва : Наука, 2006. – 247 с.

• 2.    Bольмир, А. С . Оболочки в потоке жидкости и газа : Задачи гидроупругости / A. С. Вольмир – Москва : Наука, 1979. – 387 с.

• 3.    Сейранян, А. П. Оптимизаци флаттерных характеристик / A. П. Сейранян, A. В. Шаранюк // Труды Aрмянской Aкадемии Наук. – 1984. – Т. XXXYII, № 5. – С. 38–50.

• 4.    Чугунов, M. B. Aнализ сверхзвукового флаттера осесимметричной оболочки с меридианом в виде сплайна в среде SolidWorks на базе API [Электронный ресурс] / М. В. Чугунов // Наука и образование : электронное научно-техническое издание. – 2012. – № 4. – URL: http://technomag . edu.ru/doc/348787.html.

• 5.    Чугунов, M. B. Программный модуль для решения задач оптимального проектирования в среде SolidWorks на базе API [Электронный ресурс] / М. В. Чугунов, Ю. A. Небайкина // Наука и образование : электронное научно-техническое издание. – 2011. – № 9. – URL: http://technomag.edu.ru/ doc/206217.html.

• 6.    Экспериментальное наблюдение одномодового панельного флаттера в сверхзвуковом потоке газа / В. В. Веденеев [и др.] // Доклады академии наук. – 2009. – Т. 427, № 6. – С. 768–770.

• 7.    Vedeneev, V. V. Numerical analysis of single mode panel flutter in a viscous gas Flow / V. V. Vedeneev // Proceedings of the ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting and 8th International Сonference on Nanochannels, Microchannels, and MinichannelsFEDSM-IСNMM2010. – pp. 1–6.

• 8.    Polynkin, A. Mid-range metamodel assembly building based on linear regression for large scale optimization problems. / A. Polynkin , V. V. Toropov // Structural and Multidisciplinary Optimization. – 2011. – № 4. – pp .1–13.

• 9.    Powell, M. J. D. A fast algorithm for nonlinear constrained optimization calculations / M. J. D. Powell // Report DAMTP 77/NA 2, University of Сambridge. – 1977.

• 10.    Toropov, V. V. Multipoint approximation method in optimization problems with expensive function values / V. V. Toropov // In: Sydow, A. (ed.) Сomputational Systems Analysis, Elsevier. – 1992. – pp. 207–212.

• 11.    Chugunov, M. V. Optimization of axisymmetric shells for flutter / M. V. Сhugunov, V. P. Malkov, E. N. Batrakov, V. V. Toropov // Proc. of 1st ASMO UK / ISSMO Сonf. on Engineering Design Optimization. Ilkley, MСB University Press. – 1999. – pp. 119–125.

• 12.    Chugunov, M. V. Optimization of axisymmetric thin-walled shells with flutter constraints by simulation approach method and sensitivity analysis / M. V. Сhugunov, V. P. Malkov // Transaction of St-Petersburg academy of sciences for strength problems. – 1997. – Vol. 1. – pp. 93–100.

В статье решается задача о сверхзвуковом флаттере осесимметричной оболочки при числах Маха, больших 1.7. Рассматриваемая оболочка является элементом составной конструкции вращения, и образующая ее задана Безье-сплайном. В качестве метода решения используется МКЭ. Приводится решение тестовых задач.

В работе представлена методика и ее программная реализация для решения задач оптимального проектирования на базе API SolidWorks. В процессе решения задачи функции оптимизации поэтапно аппроксимируются упрощенными аналитическими зависимостями, анализ которых не требует больших вычислительных затрат. Приложение реализовано в виде AddIn DLL-модуля, функционирующего в адресном пространстве SolidWorks и использующего COM-интерфейс.

Поступила 19.01.2015 г.

Об авторах:

The problem of supersonic flutter of an axisymmetric schell for Mach number greater then 1.7 is solved in the article. This shell is an element of a complex structure of rotation, and its meridian is formed with Bezier-spline. FEM is used for the analysis. Solutions of test tasks are provided.

The method and its program realization for the solution of optimal design problems on the basis of API SolidWorks are presented in this paper. In the course of the solution of this problem the functions are approximated step by step by the simplified analytical dependences, which do not demand big computing expenses for the analysis. The appendix is realized in the form of AddIn of the DLL module functioning in address space of SolidWorks with usage of the COM-interface.

Submitted 19.01.2015

About the authors: