Выделение гироскопических инерционных сил из центробежных и кориолисовых инерционных сил

Для управления механическими системами (МС), например, манипуляционными системами промышленных роботов, широко используются уравнения динамики (УД) [1, 2]. Эти УД чаще всего выводятся по формализму Лагранжа [3–5], реже по формализму Аппеля и другим формализмам [6]. Для использования формализма Лагранжа необходимо знать выражение Лагранжиана, т. е. разности кинетической и потенциальной энергии. Выражением кинетической энергии МС является квадратичная форма обобщенных скоростей, коэффициентами которой являются элементы матрицы инерционных коэффициентов (МИК). Вывод элементов МИК для МС с тремя и более подвижными телами является сложной и громоздкой задачей. Не менее сложно применять к кинетической энергии формализм Лагранжа. Поэтому в учебной и научной литературе чаще всего выводятся УД плоских двухзвенников [7–10]. Рассматриваются также конкретные МС [11–13] и их классы [14].

Несколько новых методов выписывания элементов МИК изложено в книге [15]. Там же по формализму Лагранжа выведены общие формулы для автоматического выписывания обобщенных инерционных сил (ОИС). В конкретных примерах, демонстрирующих эффективность предложенного формализма выписывания УД, из ОИС выделены гироскопические инерционные силы (ГИС). Но общие формулы отдельного выписывания центробежных инерционных сил (ЦИС), кориолисовых инерционных сил (КИС) и выделения среди них ГИС в книге [15] отсутствуют. В настоящей статье этот пробел устранен.

Постановка задачи. В статье ставится задача вывода общих формул для выписывания ОИС в виде суммы ЦИС, КИС и ГИС для произвольных механических систем с голономными стационарными связями и их распространения на два класса систем тел (СТ), на древовидные СТ с открытыми ветвями (ДСТОВ) и на СТ с одной открытой ветвью (СТОВ). В структуре формул для ДСТОВ и СТОВ должны быть явно выделены номера тел, движения которых порождают указанные ОИС. Эффективность предлагаемых формул можно продемонстрировать на примерах ручного выписывания ЦИС, КИС и ГИС ДСТОВ для типовых манипуляторов промышленных роботов.

1. Формализмы выписывания ОИС

Введем обозначения:

q i - i-я обобщенная скорость (ОС);

H ji - элементы симметричной (H ij = H j{ ) положительно определенной матрицы инерционных коэффициентов (МИК);

q₁, q₂,...,q_N — обобщенные координаты (ОК);

Hjik = 9Hji/ dqk, j > i.

Утверждение 1 . УД механической системы с голономными стационарными связями представимы в виде

S j=i ^Hij^qj + ^Hii^qi + ^=1+1 ^Hji^qj + ^qd + ^q _O i + h_g i = Q gi ,                                (1)

где i = 1,2, ...,N; Q_g i - i-я обобщенная движущая сила, включающая силу тяжести;

hci = 0,5Hiiiq?+^.i+iHjijqj(2)

- ЦИС(1) - центробежная инерционная сила, действующая на l-е тело;

hOi = 0,5qi I%i Hujqj + Ij^ qj I".i Hjikqk(3)

- КИС(1) - кориолисова инерционная сила, действующая на l-е тело;

дТ/ dqi = 0,5 I^=i Hjjiqj + Ik 2 qk Ijzi Hkjiqj;(4)

hgi = ТЙ Hijqj + 0,5Huqi - дТ/ dqi(5)

– ГИС(i) – гироскопическая инерционная сила, действующая на i -е тело.

В формуле (3) запись N/l в верхнем пределе суммирования указывает на то, что индекс суммирования не принимает значение l. Аналогично трактуется запись N/j.

Доказательство . Кинетическая энергия механической системы (МС) с голономными стационарными связями представима в виде

Т = 0,5 I^ Hjjqj + I^ qk I^Zi Hkjqj, где в общем случае элементы МИК зависят от всех ОК. Из выражения Т получим дТ/ dqi = Ij.i Hijqj + Huqi + I^. Hnq$.

Согласно формализму Лагранжа УД МС представим в виде [16]

(дТ/ dq i )_t - дТ/ dq i = S /.i H ij q j + H_uq_t + I^ H ji q j + h i = Q_g i , где h i - l-я обобщенная инерционная сила (ОИС), вычисляемая по формулам:

hi = hai + hbi + hpi — дТ/ дqi, hai = I. Hijqj, hbi = Huqi, hpi = I!j-i+i Hjiqj,                                                                              (6)

ат aqt = hdi + hei, hdi = 0,5I^i Hjjiqj, hei = Ik=2 qkIj=i Hkjiqj.

Из формул (6) следует искомая формула (4).

Выделим из ОИС гироскопические составляющие, т. е. ГИС. Для этого выполним следующие очевидные преобразования:

I i.i Mi = I^ q i I ^=2 q k I jZ H kji q j =

= I ^.2 q kIM q j^^i H kji q i = I^ q i I j^l q j H ij .

I^ (h ai - h ei )q i = I^ i q i l j~A H ij q j - ^ q i I j^i q j H ij = 0.

Следовательно, по определению Тэта (мощность ГИС равна нулю [16]) выражение h_a i - h_e i входит в формулу вычисления ГИС(1). Аналогично

I^i hdiqi = 0,5I^i qiI^.i Hjjiqj = 0,5IjCi qj I^i Hjjiqi = 0,5I^ Hjjqj.

H^ (0,5h bi - h₁ i )q i = 0,5 1 .i Й„я ? - 0,5I ^.i H_nq j = 0, т. е. выражение 0,5h bi - h ^i входит в формулу вычисления ГИС(1).

Таким образом, hi = 0,5hbi + hpi + hgi, где формула вычисления ГИС имеет вид hgi = hai - hei + 0,5hbi - hdi = hai + 0,5hbi - дТ/ дqi, что с учетом обозначений (6) доказывает искомую формулу (5).

Выражение 0,5h bi + h_p i , не входящее в ГИС(1), представим в виде суммы h_c i + h_O i , где h_c i - ЦИС, h_O i - КИС. Для этого в выражениях h bi , h_p i выделим слагаемые с квадратами ОС.

Эти слагаемые составляют ЦИС. Оставшиеся слагаемые составляют КИС. Используя обозначение (6), получим

0,5h_bi + h_pi = 0,5Н^ + J Li+i H jt q j =

= ^0,5qf L k^l ^Hiik^qk ⁺ E y^i+i ^qj^{l N} =i ^Hjik^qk = ^hci ^{+ h}oi , где

• ^hci = ^0,5Hiii^qi + ’L^Ij=i+i ^Hjij^qj ,

• ^hoi = 0,5 ^qi E fc^l ^Hiik^qk ⁺ E j^i+i ^qj^{l N} ^I ^Hjik^qk ,

что совпадает с искомыми формулами (2), (3). Утверждение доказано .

Рассмотрим древовидные системы тел с открытыми ветвями (ДСТОВ), состоящие из поступательных и вращательных кинематических пар, где в качестве ОК приняты относительные линейные и угловые величины. В ДСТОВ каждое тело имеет несущие и несомые тела. В случае подсистемной нумерации тел ДСТОВ знак суммирования величины O j по номерам тел, несущих i-е тело, записывается в виде j j ^-1 O j и знак суммирования величины O j по номерам тел, несомых i-м телом, записывается в виде lN=i_+I O j , где N i - номер последнего тела i-й подсистемы ДСТОВ [15].

Утверждение 2 . УД ДСТОВ с подсистемной нумерацией тел представимы в виде

• ^{1    1 H}ij^qj ^{+ H}ii^qi ⁺ E y^i+i ^Hji^qj ^{+ h}ci ^{+ h}oi ^{+ h}gi = ^Qgi ,

где i = 1,2,..., N;

hci = I-^i+i Hjijqj(7)

• -    ЦИС(i), действующая на i-е тело и зависящая от квадратов ОС его несомых тел;

hoi = h0i + ^j^^i+i qjIk=i+2 Hjikqk

• -    КИС(i), действующая на i-е тело и зависящая от произведений разноименных ОС его несомых тел, а также от произведения ОС i-го тела на ОС его несомых тел;

hgi h; - V ■ Hijqj — дТ/дЯ1(9)

• -    ГИС(i), действующая на i-е тело и зависящая, во-первых, от квадратов ОС его несущих тел, во-вторых, от произведения ОС i-го тела на ОС его несомых тел, в-третьих, от произведений разноименных ОС его несущих тел на ОС как несущих, так и несомых тел;

hgi = 0,5qiE;,:ii+iHiijqj

• -    составляющая КИС(Г) и ГИС(i), действующая на i-е тело и зависящая от произведения ОС i-го тела на ОС его несомых тел.

Доказательство . Общий вид УД для ДСТОВ получается из формулы (1) путем использования записей сумм по номерам несущих и несомых тел.

В ДСТОВ с подсистемной нумерацией тел H jj зависит от q j _+i, q j ₊₂, •••, q_Nj , H kj зависит от q j _+i, q j ₊₂, ...,q k , q k _+i, ..., q_Nk и в обозначении H kji индекс i должен быть больше индекса j [15]. Поэтому для ДСТОВ формулы (2), (3) принимают вид:

hci = Ey^i+i Hjijq7?, hoi = 0,5qilNLi+i Hiijqj + lNii+i qjI^+2 Hjikqk, что с учетом обозначения (10) совпадает с формулами (7), (8).

Для ДСТОВ из формулы (5) получим hgi = I j-1 Hijqj + 0,5qi iN^i+i Hiijqj — дТ/ dqi, что с учетом обозначения (10) совпадает с формулой (9). Утверждение доказано.

Рассмотрим системы тел с одной открытой ветвью (СТОВ). Для них цепочка тел с номерами 1,2,...,i — 1 является несущей для i -го тела и цепочка тел с номерами i + 2, i + 3,... ,N является несомой i-м телом.

Утверждение 3 . УД СТОВ представимы в виде

Sj-i H^jQj + HuQi + 2y-i+i Hj^Qj + hc( + hoi + hg^ — Qg^, где i — 1,2,...,N;

hd — ^=i+i Hjtjqj;(12)

hot — hsoi + Ij^i Qj iN-j+i (Hki]- + Hjik)qk;(13)

9Т/ dqt — 0,5 lj-\ Hjjtqj + Sj-i Qj iN-j+i H^qk(14)

hgt — h90i + Ijzi Htjqj - дТ/ dqt;(15)

hsot — 0,5Hitqi — 0,5qt lN=t+i H^;(16)

hcN — hoN — hs0N — дТ/ dqi — 0;  hoi — hgi — h90i.(17)

Доказательство . Для СТОВ элементы H kj МИК, где k >  j, зависят от q j _+i, q j ₊₂, •••, q_N [15].

Следовательно, для СТОВ формулы (7), (9), (10) принимают искомый вид (12), (15), (16).

Для доказательства формулы (13) преобразуем двойную сумму в формуле (3) с учетом структурных свойств СТОВ. Получим

S N-i+i q j l N=i H jik q k — I .N=ui q j^k-i H jik q k + S N-j+i H jik q k ).                      (18)

В первой двойной сумме изменим порядок суммирования по формуле (2) приложения 1 книги [15]. Тогда получим lN-i+i ^^k-i Hjikqk — lN-i+i qklN-k+i Hjikqj — lN=i+i qjIk-j+i Hkijqk. Следовательно, формула (18) принимает вид lN=i+i qjIk-/i Hjikqk — TJ—i+i qjIk-j+i Hkijqk +lN-i+i qjlN-j+i Hjikqk и формула (3) для СТОВ представляется в искомом виде (13). Утверждение доказано.

• 2.    Примеры выписывания ОИС

Рассмотрим примеры выписывания по формулам (11)–(17) УД СТОВ с явно выраженными ЦИС, КИС и ГИС.

В УД используются моменты инерции тел относительно осей их связанных систем координат (ССК). Для сокращения записей будем считать, что ССК i -го тела, т. е. ССК(i), является главной для i-го тела и два осевых момента инерции тела совпадают. Обозначим через I j^ ,i f , i f осевые моменты инерции i -го тела, т. е. i f - момент инерции i -го тела относительно оси O i X i , i f - момент инерции i -го тела относительно оси O ^ y, i f - момент инерции i -го тела относительно оси O jZi , где Xi, ^, , Z i - орты CCK(i), O i - полюс i-го тела.

Условимся вводить ССК тел так, чтобы в исходном положении СТОВ, т. е. для нулевых значений ОК, оси CCK(i) были параллельны соответствующим осям неподвижной СК, в которой ось абсцисс Ox направлена горизонтально вправо, ось ординат Оу направлена вертикально вверх и ось аппликат Oz - на нас. В кинематических схемах СТОВ тела вращательных кинематических пар будем изображать в исходных относительных положениях, т. е. когда их ОК равны нулю.

Для упрощения процесса выписывания ОИС введем в обращение таблицу ОК (ТОК). Заголовок ТОК содержит обозначения номера строки к и столбца j МИК, на пересечении которых расположен элемент H kj , где к >  j. За числами к и j в порядке возрастания номеров перечислены ОК, от которых зависят элементы МИК, т. е. циклические ОК в ТОК не записываются. Под заголовком проведена двойная горизонтальная линия. ТОК разбита на блоки, которые отделены друг от друга двойной горизонтальной линией. Номер блока равен номеру, который записан в первом столбце. Столбцы k,j отделены от столбцов ОК двойной вертикальной линией.

ТОК заполняется по следующим правилам.

• 1.    Если цифра в столбце j последней строки к -го блока равна к, то индикаторы 0 или 1 в следующих столбцах указывают на зависимость (индикатор равен 1) или независимость (индикатор равен 0) от соответствующей ОК диагонального элемента H kk .

• 2.    Если первые две цифры строки равны k, j, то следующие за ними индикаторы 0 или 1 указывают на зависимость (1) или независимость (0) элемента H kj от соответствующей ОК.

• 3.    Если элементы H_k j постоянны, где к >  j, то строка с первыми двумя числами к и j в ТОК отсутствует.

Каждый пример начинается с рисунка, на котором представлены кинематическая схема манипулятора (далее – схема), его МИК и ТОК. Схема и МИК взяты из примеров 1–6 книги [15]. На схеме изображены положения полюсов тел, каждое из которых является началом ССК тела, и положения центров масс (ЦМ) тел – в виде крестиков. В записи элементов МИК и в основном тексте используются следующие обозначения:

a t = m oi lO j C j l, где m_o t - масса i-го тела, О^ - радиус-вектор, проведенный из полюса i-го тела в его ЦМ;

m t - масса i -й подсистемы, т. е. тел с номерами i,i + 1,...,N;

q_t - орт оси вращения O t q t i -го тела;

P t - орт оси O f P t поступательного движения i -го тела относительно предшествующего тела;

st = sin(qt); Ct = cos(qt).

Здесь и далее для сокращения записи МИК опускается ее обозначение H, а вместо ненулевых наддиагональных элементов записываются их обозначения.

Аббревиатуру МС в примерах следует трактовать как манипуляционная система робота.

Пример 1 . МС с полярной СК в вертикальной плоскости на рис. 1. Для этой МС имеем:

N = 2; qt = z; р2 = х2= Xi; q2 = O^;

масса m_o t (i = 1,2) распределена симметрично оси O ^ X t .

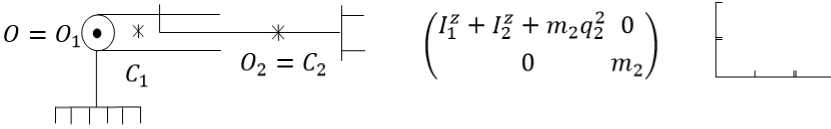
Рис. 1. Механическая система с полярной системой координат Fig. 1. Mechanical system with polar coordinate system

к	j	fP
3	1	1

По формулам (17) имеем:

hc2 = ^02 = hS02 = дГ/ dqi = 0, hoi = hgi = hSgi.

Для i = 1 по формулам (12), (16) и ТОК выпишем hCi = H2i2q2 = 0, ^oi = 0,5qlH112q2, где с учетом выражения Hii имеем Hii2 = 2m2q2.

Для i = 2 по формуле (14) выпишем

дГ/ dq2 = 0,5Hii2q2 + qiH2i2q2 = m2q2ql.

Следовательно, по формуле (15) получим

hg2 = H2iqi — дТ / dq2 = -m2q2q2.

Таким образом, УД МС на рис. 1 с выделенными ГИС имеют следующий вид:

№ + 12 + m2q2)qi + 2hgi = Qgi,

(       m2q2 + hg2 = Qg2, где qgi = m2q2qiq2, hg2 = -m2q2q2. Действительно, по определению Тэта

hgiqi + hg2q2 = m2q2q2q2 — m2q2qlq2 = 0.

Пример 2 . МС с декартовой СК в вертикальной плоскости на рис. 2. Для этой МС имеем:

N = 3; pi = у; p2 = X; q3 = z; qi = OOi; q2 = OiO2;

масса mo3 распределена симметрично оси O3X3.

По формулам (17) имеем:

hc3 = ho3 = hg3 = дГ/ dqi = 0, hoi = hgi = hflgi.

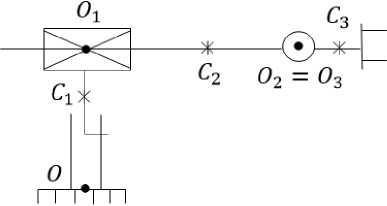
Рис. 2. Механическая система с декартовой системой координат Fig. 2. Mechanical system with Cartesian coordinate system

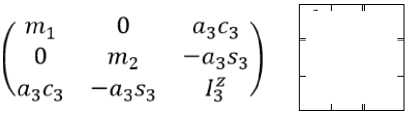
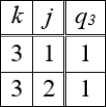
Для i = 1 по формулам (12), (16) и ТОК выпишем hc1 = ^212^2 + Н31393 = Н31393,

^о1 = 0'591(^11292 + Н11393) = hg1 = 0, где с учетом выражения Н31 имеем Н313 = — a3s3.

Для i = 2 по формулам (12), (16), ТОК и элементам МИК выпишем ^hc2 = ^Н 3239з = - ^а3^С3 9 з ,

hs02 = 0'592Н2292 = 0, ^02 = дТ/ д92 = 0, hg2 = 0.

Согласно определению Тэта, если ^ = 3 и h_g1 = h g ₂ = 0, то h g ₃ = 0.

Таким образом, в МС на рис. 2 ГИС отсутствуют и УД имеют вид

(№ 1 9 1 + ^н з19з + ^Н32 9 з = Q g1 , ^m2⁹2 + ^н з29з - ^н з19з = ^Qg2 , ^Н31 9 1 + ^Н32⁹2 + ^з9з = ^Qg3 .

Пример 3 . МС с цилиндрической СК на рис. 3 (N = 3) . Для этой МС имеем:

^ = 3; ^ = у; р2 = ^; р3 = —у; 92 = O1O2; 9з = O2O3;

массы m₀ i (для i = 1 и i = 3) распределены симметрично осям О ^ у;

масса m02 распределена симметрично оси О2%2.

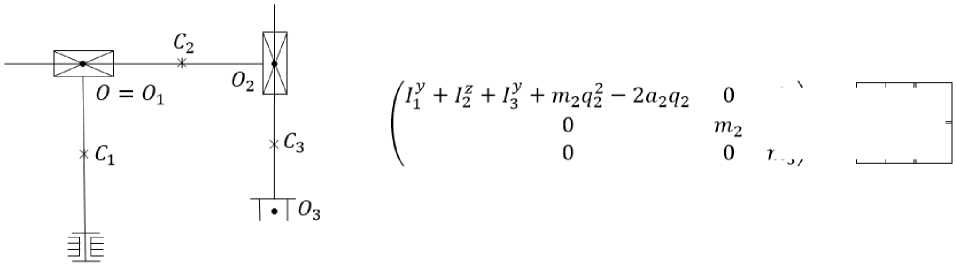
Рис. 3. Цилиндрическая механическая система ( N = 3)

Fig. 3. Cylindrical mechanical system ( N = 3)

По формулам (17) имеем

hC3 = ho3 = hg3 = дТ/ д91 = 0, h01 = hg1 = hg1.

Для i = 1 по формулам (12), (16) и ТОК выпишем ^hC1 = ^Н212⁹2 + ^Н313^{9 2} = 0, ^hg ₁ = ⁰ ' ⁵⁹1^Н112⁹2 .

С учетом выражения Н11 имеем

Н112 = 2т292 - 2^2 = 2mq2, где mq2 = №292 - «2.

Для i = 2 по формулам (12), (16) и ТОК выпишем ^hc2 = ^Н323⁹3 = 0, ^hg2 = ⁰ ' ⁵⁹2^Н223⁹3 = 0.

По формуле (14) выпишем

дТ / dq2 = 0,5H112q^ = mq2ql,hg2 = — дТ/ dq2 = —w^qi.

Таким образом, УД МС на рис. 3 с выделенными ГИС имеют следующий вид: ГUi + 12 + I3 +m2q2- 2a2q2)qi + 2hgi = Qgi, j              m2q2 + hg2 = Qg2, m3q3 = Qg3, где hgi = m^q^, hg2 = —m^i- Действительно, hgiqi + hg2q2 = m^q^ — mq2q^q2 = 0.

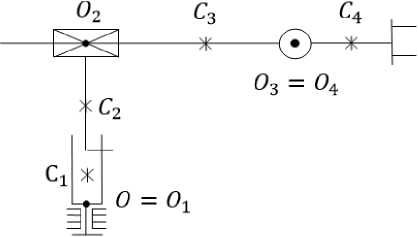
Пример 4. МС с цилиндрической СК на рис. 4 (N = 4 ). Для этой МС имеем:

^ = 4; ^ = у; р2 = у; р3 = %i; q4 = z4 = Zi; q2 = O^; q3 = O2O3;

массы m_O i (i = 1,2) распределены симметрично осям О ; у_;;

массы m_O j (j = 3,4) распределены симметрично осям O j X j .

Иц

О

О

. о

о

ТП2 о о 4 С4

оот3

ci4s4

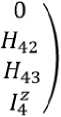
k	j	43	44
1	1	1	1
4	2	0	1
4	3	0	1

Рис. 4. Цилиндрическая механическая система ( N = 4)

Fig. 4. Cylindrical mechanical system ( N = 4)

По формулам (17) имеем

hC4 = ho4 = hs04 = дТ/ dqi = 0, hoi = hgi = h90i.

Для i = 1 по формулам (12), (16) и ТОК выпишем hCi = 0, hgi = 0,5qi(Hii3q3 + Hii4q4').

Используя МИК, получим

Hii3 = 2(m3q3 + a4C4 - Пз) = 2hq,

^Hii4 = ^2q3^(-a4^s4^{) — 2(I}4 ^{— I}4()^c4^s4 = ^-2Iq ,

где hq = m3q3 + a4c4 — a3, Iq = [a4q3 + (If — If)c4]s4. Следовательно, h0i = (hqq3 - Iqq4')qi.

Для i = 2 по формулам (12)-(16), ТОК и МИК выпишем hc2 = H323q3 + H424q4 = —a4S4q4,

hS02 = 0, ho2 = 0, дТ/ dq2 = hg2 = 0.

Для i = 3 по формулам (12)-(16), ТОК и МИК выпишем

hc3 = H434q4 = —a4C4q4, ho3 = 0, hg3 = 0,

дТ/ дqз = 0,5Hii3q12 = hqq2, hg3 = — дТ/ дqз = —hqq2.

Для i = 4 по формулам (14), (15) выпишем

дТ/дq4 = 0,5Hii4qi = —Iqqf,hg4 = —дТ/дq4 = Iqq2

Таким образом, УД МС на рис. 4 с выделенными ГИС имеют следующий вид:

/1 ^qi + ^2hgi = ^Qgi ,

rn2q2 + H42q4 + H43qi = Qg2, m3q3 + H43q4 - H42q4 + hg3 = Qg3, < H42q2 + H43q3 + I4q4 + hg4 = Qg4, где hgi = hqqiq3 - Iqq^; hg3 = -hqql; hg4 = IqQ^ Очевидно, что hgiqi + hg3q3 + hg4q4 = 0.

Пример 5. Ангулярная МС на рис. 5 (N = 3 ) . Для этой МС имеем: N = 3; q^y; q₂ = q₃ = Z i ; L = O 2 O 3 ; C 23 = cos(q 2 + ^q3 );

массы m_O i (i = 1,2,3) распределены симметрично осям O ^ y.

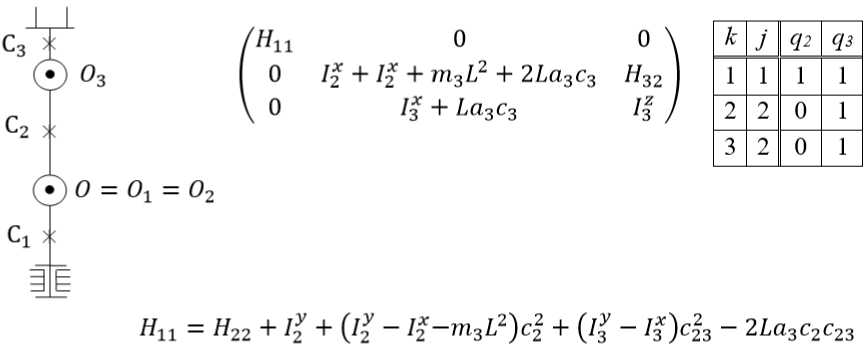
Рис. 5. Ангулярная механическая система ( N = 3)

Fig. 5. Angular mechanical system ( N = 3)

По формулам (17) имеем

hC3 = ho3 = h9O3 = дТ/ dqi = 0, hoi = hgi = h90i.

Для i = 1 по формулам (12), (16) и ТОК выпишем ^hci = 0, ^hO!i = 0, ^5qi ( ^Hii2^q2 ^+Hii3^q3⁾ .

Для i = 2 по формулам (12)-(16), ТОК и МИК выпишем hc2 = H323q3 = —La3S3ql, hO>2 = 0,5q2H223q3 = —La3S3q2q3, ho2 = h9O2, dT/dq2 = 0,5Hii2ql hg2 = hg2 — дТ/ dq2 = 0,5(H223q2)q3 — Hii2ql.

Для i = 3 по формулам (14) и (15) выпишем дТ/ dq3 = 0,5(Hii3qI + H223q2^ + q2H323q3, hg3 = H3iqi + H32q2 — ^q^ = H323q2q3 — 0,5(Hii3qI + H223q2) — q2H323q3.

Таким образом, УД МС на рис. 5 с выделенными ГИС имеют следующий вид:

^Hii^qi ^{+ 2h}gi = ^Qgi ,

H22q2 + H32q3 — La3S3ql — La3S3q2q3 + hg2 = Qg2, H32q2 + I3q3 + hg3 = Qg3.

Вычислим мощность ГИС. Получим hgiqi + hg2q2 + hg3q3 = 0,5qi(Hii2q2 + Hii3q3)qi +

⁺ 0, ^5(H223^q2^q3 ^{— H}iI2^qiL^)q2 ^{— 0} , ^5(HiI3^qI ^{+ H}223^q2^)q3 = 0.

Пример 6 . Универсальная МС с декартовой СК (рис. 6). Для этой МС имеем: W — 6; p j — z; p₂ — x; q₃ — y; p₄ — —y;

q5 — Z5; q6 — Z6; q1 — 001; q2 — 0T02; q4 — 0304;

массы m_Oi (i — 3,4,5,6) распределены симметрично дующие обозначения:

осям

использованы сле-

0_ty_t . В МИК

В

— / 5 — / 5	+ / ; —/б7
ma	0	^31	0	^51	0 \
0	m2	^32	0	^52	0 '
—ttCgSs	-ns3s5	Л "  Bel	0	0	^63
0	0	0	m4	^S4	0
—aS3Cg	ac3s3	0	-«s5	15 + 1б	0
0	0	l^s	0	0	'U

а — а 5 + а ^ ; Л — ^ + / ^ + / 5 + / 6 ;

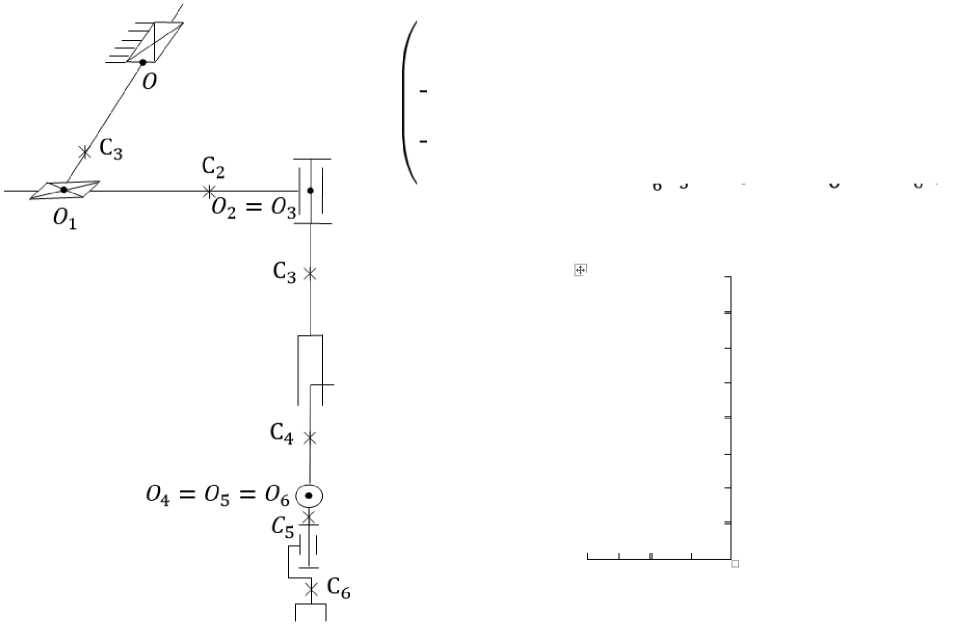
Рис. 6. Механическая система с декартовой системой координат Fig. 6. Mechanical system with Cartesian coordinate system

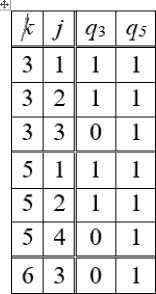
По формулам (17) имеем

hc6 — hob — hS06 — дГ/ 8q, — 0, ho1 — hgl — hOr

Для i — 1 по формуле (12) на основе ТОК выпишем отличные от нуля ЦИС. Получим ^hc1 ^— ^ 313^q3 ⁺ ^ 515^q5 , ^hc2 ^— ^ 323^q3 ⁺ ^ 525^q5 , ^hc4 ^— ^ 545^q5 .

По формуле (16) на основе ТОК выпишем

• ^ho3 ^{— 0} , ^5q3 ^ 335^q5 .

По формуле (13) на основе ТОК выпишем отличные от нуля КИС. Получим

• ^hO1 ^{— q}3⁽ ^ 513 ⁺ ^ 31s ) ^q5 , ^ho2 ^{— q}3⁽ ^ 523 ⁺ ^ 325 ) ^q5 ,

• ^h03 ^{— h}O°3 ^{+ q}5 ^ 635^q6 .

По формуле (15) на основе ТОК выпишем отличные от нуля ГИС. Получим

• ^hO3 ^{— h}03 ^+q1№13^q3 +^ 315^ ) ^{+ q}2№23^q3 +^ 325^ ) ^-дГ/^3 ,

• ^hO5 ^{— q}1⁽ ^ 513^q3 ⁺ ^ 515^q5 ) ^{+ q}2⁽ ^ 523^q3 ⁺ ^ 525^q5 ) ^{+ q}4 ^ 545^q5 ^{— дГ/ dq}5 ,

• ^hO6 ^{— q}3 ^ 635^q5 .

Таким образом, УД МС на рис. 6 с выделенными ГИС имеют следующий вид:

• г т^ - ac3s5q3 - as3c5q5 + a[s3s5(q2 + q^) - 2c3c5q3q5"\ = Qgi,

m2q2 - as3S5q3 + ac3c5q5 - a[c3s5(ql + qi2) + 2s3C5q3q5] = Qg2,

• _ -ac3S5q1 - as3c5q2 + (Л - Bcj^ + I^c^ + Bs5c5q3q5 + hg3 = Qg3, m4q4 - as5q5 - ac3qf = Qg4,

-as3c5qi + ac3c5q2 - as5q4 + (I^ + Ig)q5 + hg5 = Qg5,

• .                   Iec5q3+I^q6-I^s5q3q5 = Qg6,

где hg3 = Ibc5q3q5 - I^'s5q5q6, hg5 = I6s5q3q6 - Ibssc5q2, hg6 = q3H635q5.

ОИС принимают вид

hi = a[s3s5(q2 + qi2) - 2c3c5q3q5],

h2 = -a[c3s5(ql + qi;) + 2s3c5q3q5],

h3 = (2Ibc5q3 - I6'q6)s5q5, h4 = -ac5q5q5, h5 = (I6q6 - Ibc5q3)s5q3, h6 = -I6's5q3q5.

Заключение

Описанные формализмы позволяют выделять ОИС в произвольных механических системах. Особое значение имеет выделение ГИС, так как их мощность равна нулю, что упрощает решение ряда задач, связанных с вычислением работы, установочной и потребляемой мощности приводов, а также оптимальным управлением в смысле минимизации энергозатрат на реализацию программных движений управляемых систем тел.