Выделение главных направлений в задаче аппроксимации на основе гауссовских процессов

Для решения многих задач инженерного проектирования в различных областях промышленности необходимо уметь строить высокоточные аппроксимации многомерных зависимостей на основе данных, собранных в результате проведения натурных экспериментов и/или симуляционных экспериментов с физическими моделями.

В настоящее время для восстановления зависимостей широко распространено применение методов, основанных на. гауссовских процессах. Этот подход предполагает, что неизвестная зависимость порождена, гауссовским полем с неизвестной ковариационной функцией, принадлежащей некоторому параметрическому семейству. В рамках такой модели задача построения аппроксимации сводится к оценке неизвестных параметров ковариационной функции по имеющемуся набору данных с помощью максимизации соответствующей функции правдоподобия.

Стандартным параметрическим семейством, используемым для моделирования ковариационной функции, является гауссовская ковариационная функция (на основе взвешенного евклидова расстояния). Использование такого семейства фактически неявно означает, что верно предположение о совпадении направлений наиболее значимого изменения аппроксимируемой функции и направлений координатных осей в пространстве данных. Очевидно, что это предположение является достаточно ограничивающим и не всегда, выполняется в реальных задачах. Для того чтобы снять указанное ограничение и сделать модель данных более общей, было предложено использовать ковариационную функцию на основе расстояния Махалоиобиса [7]. Однако такой подход не позволяет работать с данными высокой размерности («проклятье высокой размерности», см. [4]) в связи с существенно большим числом параметров ковариационной функции, которые необходимо оценивать. Таким образом, актуальна задача разработки алгоритма настройки параметров ковариационной функции на. основе расстояния Махаланобиса, который бы позволял проводить эффективную настройку параметров и в случае данных высокой размерности.

В данной работе предложен новый алгоритм подстройки параметров ковариационной функции на. основе расстояния Махаланобиса, позволяющий эффективно решить поставленную выше задачу. Кроме того, разработанный подход позволяет линейно снизить размерность данных в некоторых задачах, выделив главные направления изменения аппроксимируемой зависимости.

Работа, устроена, следующим образом. В разделе 2 приведены основные обозначения и кратко изложена, суть метода, аппроксимации на. основе гауссовских процессов. В разделе 3 предложен новый метод оценки параметров ковариационной функции гауссовского процесса. на. основе расстояния Махаланобиса. В разделе 4 приведен подход к решению задачи эффективного снижения размерности на основе предложенного метода выделения главных направлений изменчивости аппроксимируемой зависимости, описан статистический тест для оценки размерности сжатия. В разделе 5 приведены результаты вычислительных экспериментов на искусственных и реальных данных.

2.    Регрессия на основе гауссовских процессов

Задача аппроксимации многомерной зависимости ставится следующим образом. Пусть y = J (x) — некоторая неизвестная функция со входом x G X С R^m и вы ходом y G R¹, Di_earn = ( X, У) = {(x_i, y_i = J (x_i) ,г = 1,W} — обучающая выборка. Задача состоит в построении аппроксимации y = J(x) = J(x|Di_earn) для исходной зависимости y = J(x) по обучающей выборке Di_earn.

Если для всех x G X (не только для x G Di_earn) имеет место примерное равенство

J(x) ~ J(x),

то считается, что аппроксимация хорошо воспроизводит исходную зависимость. Выполнение соотношения (1) проверяют на. независимых тестовых данных D_test = (X*, У*) = {( Xj, yj = J (xj )) , j = 1,7V*}, оценивая качество построенной аппроксимации с помощью среднеквадратичной ошибки:

N*

e(JlDtest) =

A ^r£(yj — J(xj))2•

N * j=1

2.1.    Гауссовские процессы

Гауссовский процесс является одним из возможных способов задания распределения на пространстве функций. Гауссовский процесс J(x) полностью определяется своей функцией среднего m(x) = E[J(x)] и ковариационной функцией cov(y, y' ) = k(x, x') = E[(J(x) — m(x))(J(x') — m(x'))]. Если положить функцию среднего нулевой m(x) = E[J(x)] = 0, а ковариационную функцию считать известной, то функция апостериорного (для заданной обучающей выборки) среднего значения гауссовского процесса в точках контрольной выборки X* имеет вид [6] J(X*) = К*К ^-1У, где К* = К (X*,X) = [fc(xi, Xj ),г = MV*,j =ІЛ],К = К (X,X) = [fc(xi, Xj ),i,j =ІЛ ].

Обычно предполагается, что данные наблюдаются с шумом: y(x) = J(x) + e(x), где e(x) ~ N (0, Т2) — белый шум. В так ом случае наблюдения y(x) являются реализацией гауссовского процесса, с нулевым средним и ковариационной функцией cov(y(x), y(x')) = k(x, x') + T 25(x — x'), г де 5(x) — дельта-функция. Таким образом, функция апостериорного (для заданной обучающей выборки) среднего значения гауссовского процесса f (x) в точках контрольной выборки X* принимает вид

f(X*) = к*(к + a²I )^-1У,                              (3)

где I — единичная матрица, размера. N х N.

Заметим, что наличие в формуле (3) дисперсии шума a ² фактически приводит к регуляризации, что позволяет улучшить обобщающую способность аппроксиматора. При этом апостериорная ковариационная функция гауссовского процесса в точках контрольной выборки имеет вид

V[X*] =к(X*,X*)+a²I* -к*(к + a²IГк¹.,                (4)

где к(X*,X*) = [k(x_i, Xj),i,j = 1,..., N*], I* — единичная матрица размера N* х N*.

Дисперсии гауссовского процесса, в точках контрольной выборки могут быть использованы как оценки ожидаемой ошибки аппроксимации в этих точках. Заметим, что для этого нет необходимости вычислять по формуле (4) всю матрицу V[X*], а достаточно вычислить только элементы ее главной диагонали, которые и являются искомыми дисперсиями.

Кроме того, зная среднее и ковариационную функцию, можно также получить апостериорную оценку среднего и дисперсии производной гауссовского процесса, в точках. Если df(x)I

Эх Ix=xo, то Law (g(xo)|(X, У)) = N (Jт (к + a2I )-1У, В -Jт (к + a21)-1J), где

J^т =

dk(xo - xi)     Әк(хо - x_n)

d xo      ^,.",     dxo

В =

cov(g1(xo),51(xo))

cov(g1(xo),gm(xo))

. cov(gm(xo),51(xo))

cov(gm(xo),gm(xo)Y

^cov⁽gt,gj ) =

8²k(xo, xo) dx^ldx^j

gi — i-я компонента вектора градиента g.

2.2.    Оценка параметров гауссовского процесса

При работе с реальными данными ковариационная функция породившего их гауссовского процесса, как правило, неизвестна, поэтому необходимо уметь идентифицировать ее по данным.

Предположим, что ковариационная функция гауссовского процесса, принадлежит некоторому параметрическому семейству k(x, x‘) = k(x, x'|a), где a G R^ — вектор параметров ковариационной функции. Семейство k(x, x‘|a) обычно берется из класса так называемых стационарных ковариационных функций, т.е. функций, значения которых зависят только от разности значений аргументов k(x,x‘|a) = k(x — x'|a). Стандартный способ оценки значений параметров а по обучающей выборке Diearn состоит в использовании принципа. максимума, правдоподобия. Логарифм правдоподобия гауссовского процесса, в точках обучающей выборки [6] при этом имеет вид log р(у|X, a,a) = -2ут(к + a2i)-1у - 2 log |к + a2iI - ^2 log 2т, (5)

где |к + a²I| — детерминант матрицы к + a²1

Кроме параметров а ковариационной функции, параметром функционала (5) является также значение дисперсии шума наблюдений ст², которое также можно настраивать по обучающей выборке. Таким образом, нахождение оптимальных значений параметров сводится к отысканию максимума правдоподобия по параметрам log р(У |X, a, a) ^ max_a,5-.

2.3.    Ковариационная функция

Выбор конкретного семейства ковариационных функций k(x, x '|a) обычно продиктован соображениями удобства, а также априорными представлениями о свойствах аппроксимируемой зависимости.

Для моделирования ковариационной функции часто используется экспоненциальное семейство K q(x , x ') = (г^ exp(— d(x, x')), где d(x, x) — расстояние между точками x и x ' в некоторой метрике. Наиболее распространены два. типа, расстояния:

• •    Взвешенное евклидово расстояние

m

d(x, x') = ^ Ө^х¹ - (ж')")², x = (аЛ ••• ,^^m),                    (6)

г=1

где Ө" Е R, г = 1,m. При использовании такого расстояния возникает необходимость настроить m параметров Ө1,..., Ө_т.

е Расстояние Махалонобиса

d(x, x) = ( x — x ' )^T A( x — x '),                             (7)

где А Е Rmxm — некоторая положительно определенная матрица. Для параметризации этой матрицы в силу положительной определенности А можно использовать разложение Холецкого А = LTL, где L — верхняя треугольная матрица с положи тельными элементами на. главной диагонали. В таком случае необходимо настроить m(m+1)

—^—- параметров, зі ідаюттіих матрицу L.

В работе [7] показано, что использование ковариационной функции на. основе расстояния Махаланобиса обеспечивает инвариантность точности аппроксимации по отношению к степени коллинеарности направлений наиболее значимого изменения аппроксимируемой функции и направлений координатных осей в пространстве данных. В то же время при использовании ковариационной функции на. основе взвешенного евклидова, расстояния получаются аппроксимации, точность которых существенно зависит от взаимного расположения направлений наибольшей изменчивости аппроксимируемой зависимости и координатных осей в пространстве данных. Однако качество построенных моделей, испольующих ковариационную функцию на. основе расстояния Махаланобиса, существенно ухудшается с ростом размерности. Это связано с квадратичным ростом числа, настраиваемых параметров при увеличении размерности задачи.

3.    Выделение значимых направлений через аппроксимацию градиента

В этом разделе описан подход к оценке параметров ковариационной функции на. основе расстояния Махаланобиса, который позволяет проводить эффективную настройку параметров и в случае данных высокой размерности.

При определении ковариационной функции типа. (7) на. основе расстояния Махаланобиса. можно использовать следующую параметризацию1:

d(x, x') = (x — x')TBTЛB(x — x'), где B — ортогональная матрица m x m, Л — диагональная положительно определенная матрица размера m x m. При такой параметризации матрица B осуществляет поворот осей координат, а диагональная матрица Л регулирует ширину ядер вдоль новых повернутых осей.

Если матрица В фиксирована и известна, то аппроксимацию / можно искать в виде f (х) = д(хВ), где g — аппроксимация на основе гауссовских процессов, использующая функцию ковариации на основе взвешенного евклидова расстояния (6). В таком случае достаточно оценить только гиперпараметры (диагональную матрицу весов Л) ковариационной функции соответствующего гауссовского процесса.

Если матрица Л фиксирована, то матрицу В можно оценить из следующих соображений. Пусть по исходной выборке построена аппроксимация / на основе гауссовских процессов. Это дает нам возможность получить оценки градиентов / в точках выборки X:

{N df(x) I УМI 1 Х = М Хтх ЭХ1 lx=x,,■■■, Эхт lx=xj. ’ Х (Х - )•

В таком случае мы можем развернуть координатные оси так, чтобы производные вдоль них не были скоррелированы между собой, т.е. найти В как собственные векторы матрицы г^Т г.

Таким образом, базовый алгоритм оценки гиперпараметров Ви Л состоит из следующих шагов:

• •    Строим аппроксимацию / на основе гауссовских процессов по выборке Di_earn.

df (x) I               Әf (x) I      1 ^N

• •    Вычисляем градиенты аппроксимации Г =    ^1 |    , • • •, g^ m |    J в точках

обучающей выборки.

• •    Вычисляем матрицу ковариации градиентов Ер = Г^ТГ.

• •    Вычисляем матрицу В собственных векторов Ер.

• •    «Поворачиваем» входные векторы выборки Di_earn, получаем новую выборку Dlearn = ZY ) = {( z = Х,В^Т, у ,) , г = I?N}.

е Настраиваем веса во взвешенном евклидовом расстоянии с помощью максимизации правдоподобия выборки Di_earn для соответствующего гауссовского процесса. Полученные значения весов используются в качестве оценки матрицы Л.

Возможно дополнительно улучшить качество итоговой аппроксимации через итеративное вычисление В:

• •    Зададим t = 1, х⁽⁰⁾ = х,, (г = 1,• • •, N), Во = I, где I — единичная матрица.

• •    По выборке данных {х^{(/ 1)}, у,}^ оцениваем матриц у проектирования В, используя базовый алгоритм.

• •    Пересчитываем итоговую матрицу проектирования согласно формуле В^ = В • В^г-

• •    Проектируем х, из текущего базиса в базис, заданный Вр х^ = х,В^Т, г = 1, • • •, N,

• •    Если мы достигли последней итерации, то останавливаемся; иначе t = t + 1, и переходим к шагу 2.

4.    Эффективное снижение размерности на основе гауссовских процессов 4.1.    Задача эффективного снижения размерности

В таком случае итоговый поворот можно записать как В = И, Вд Построение аппроксимации на основе новой выборки Di_earn = ( Z, Y) = { (z , = х ,В ^Т, у ,), г = 1,N} с «повернутыми» векторами входов зачастую существенно увеличивает точность аппроксимации.

В этом разделе приведена постановка задачи эффективного снижения размерности, а также показано, что алгоритм, предложенный в предыдущем разделе, позволяет ее решить.

Пусть процесс, порождающий данные, имеет вид y = f ( х ) + е( х ), где предполагается, что f ( х ) = g(xB^T ), е — случайный шум с Ее = 0 и В G R^cixm, d <  m, ВВ^Т = Idxd-

Под задачей эффективного снижения размерности [19] понимают задачу нахождения выпуклой оболочки 5 = 8рап{В}, которая задает центральное среднее подпространство регрессии.

Пусть В — оценка матрицы В, тогда должно быть выполнено следующее равенство:

f (хВ^ТВ) « f (х)                                 (8)

Если В содержит в себе центральное среднее подпространство, т.е. В G 8рап(В) то равенство (8) выполняется в точности.

Пусть {31, P2,... ,P_m} - собственные векторы, a {A1 > A₂ > • • • > A_m} - соответствующие им собственные числа матрицы Ер = Г^ТГ, полученные в алгоритме поворота координатных осей, описанном в разделе 3.

Если для некоторого к выполнено, что Ai ~ 0,г > к, то рассматриваемая аппроксимация имеет почти нулевую производную вдоль направлений Pi,г > к, т.е. значение функции f (х) слабо меняется вдоль направлений Pi, г > к. Значит, возможно снизить размерность входных данных, спроектировав данные на линейное подпространство В, составленное из собственных векторов матрицы Ер, соответствующих наибольшим собственным числам. При этом «потеря информации» об аппроксимируемой функции будет минимальной.

4.2.    Оценка эффективной размерности данных

В случае применения предложенного подхода эффективная размерность данных (то есть размерность центрального среднего подпространства) определяется рангом матрицы Г градиентов модели. Таким образом, оценка рекомендуемой размерности данных для процедуры снижения размерности, сформулированной в предыдущем разделе, сводится к определению размерности линейного подпространства, натянутого на. столбцы матрицы градиентов.

В литературе предложено большое количество подходов к оценке эффективной размерности данных для рассматриваемой постановки задачи.

При использовании метода, главных компонент часто в качестве оценки требуемой размерности используют число компонент, объясняющих заданную долю дисперсии данных [5]. Оценка, доли объясненной дисперсии в свою очередь равна, доле суммы наибольших у^^ д _ к собственных чисел, т.е. tk = ^m1 3. Достаточное значение t^ обычно задается внешним г=1 Лг для процедуры образом и никак не учитывает особенностей конкретных данных. На практике часто выбирают значения между 70% и 99%.

В [14] описывается тест на. сферичность. Тест основан на. том, что если вся значимая дисперсия объяснена, выбранными главными компонентами, то в дополнении к подпространству, задаваемому матрицей В, дисперсия изотропна и разброс данных в этом подпространстве может быть представлен многомерной сферой. При заданном к проводится тест на. равенство между собой собственных значений.

Близкий подход предлагается в [20]. Здесь используется то обстоятельство, что если присутствуют два. одинаковых собственных числа, то соответствующее им двумерное подпространство будет устойчиво к возмущениям выборки, однако главные направления в нем будут нестабильны. С помощью бутстрепа. можно сгенерировать набор случайных реализаций выборки. Размерность многомерной сферы, содержащей оставшуюся дисперсию, может быть найдена, из тех соображений, что оценка, этого подпространства, по различным бутстреп-реализациям будет наиболее стабильной.

В [10,18] предлагается универсальный подход, позволяющий оценить ранг матрицы В линейного проектирования, если ее оценка В оказывается асимптотически нормально рас- пределенной и несмещенной (например, в работе приведен явный вид теста на размерность данных для метода эффективного снижения размерности SIR [8]).

Далее опишем статистический тест для предложенного подхода к эффективному снижению размерности, позволяющий оценить размерность искомого подпространства.

Так как данные являются некоторой реализацией нормального поля, то для оценки ранга можно применить общие результаты из [10,18], которые позволяют проверять гипотезу о ранге случайной матрицы.

Пусть параметры случайного гауссовского поля заданы, то есть известно совместное распределение У — JV(ц, К), У = (yi,..., yN ). В таком случае матрица градиентов апостериорных средних рассматриваемой зависимости /(х) имеет безусловное распределение:

Г = {d/^l  --^l Г   ^V (^J К-1Ц'

0X1 Іх=х^г OX^m Іх=хЮ i=1

где X = Jт К-1 J, матрица J имеет вид J = [ J^, J2,..., J^ ]т, Ji — матриц а размера т х N вида Ji = ^kx)!    , k(x) = {К (x, xi )}г=г x=xl

Выпишем сингулярное разложение матрицы Г = UDV, где U — ортогональная матрица размера N х N, V — ортогональная матрица размера т х т, D — диагональная матрица размера, N х т.

Если исходная матрица В на самом деле имеет ранг к, то можно представить матрицу D в вило

D=ID где Di — невырожденная диагональная матрица размера к х к, D^ — матрица размера

(N — к) х (т — к). элементы которой должны равняться тмю. Аналогично U =  ¹

U2

U1 II U2 имеют размер к х N и к х (N — к). V = [V1  V2]. матрицы V1 ii V2 имеют размер т х к ii т х (т — к).

Используя результаты [10,18], можно показать, что если l = xec(U2^ ГЕ2)> г де нес() — вектор, составленный из элементов соответствующей матрицы, и Q = (V0U2 )X(V20U₂), где 0 - произведение Кронекера, то 1 ^{T q}I ^- Х^^-к^к-к), rankly

Заметим, что для вычисления l и Q и последующей оценки ранга можно считать гра-лиепт не во всех N точках, а доста точно рассмотреть только N *. т < N * <  N точек. В таком случае процедура оценки сводится к последовательной проверке критерия ^2 для величины l^T Ql и различных размерностей к начиная с единичной.

5.    Экспериментальные результаты5.1.    Устойчивость к повороту осей

Продемонстрируем предложенный подход на. примере функции Mystery (рис. 1):

у = 2 + 0.01(x2 — X2)2 + (1 — X1)2 + 2(2 — x2)2 + 7 sin(0.5x1) sin(0.7x1x2), где X1 G [0, 5] 11 x2 G [0, 5].

Пусть задана некоторая случайная выборка данных Di_ea/rn = {хг, уг}⁸=1, порожденная рассматриваемой функций. Будем строить аппроксимации по этой выборке в виде У = / (xV ^т ). где

V = [^cosy sin у

— sin у cos у

есть матрица поворота осей координат на угол у.

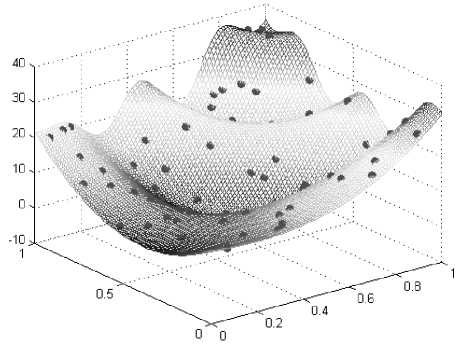
Рис. 1. Функция Mystery

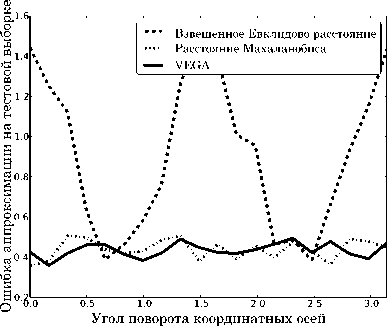
Рис. 2. Чувствительность аппроксимации к повороту координатных осей

На рис. 2 изображена зависимость качества модели от угла поворота осей координат у для различных способов задания расстояния в ковариационной функции². Под качеством модели понимается среднеквадратичная ошибка, аппроксимации на. тестовой выборке (2).

Оценка, гиперпараметров аппроксимации, использующей ковариационную функцию на. основе расстояния Махаланобиса, с помощью стандартного и предложенного подходов позволяет добиться независимости качества, модели от поворота, осей координат. В приведенном двумерном случае стандартный и предложенный в данной работе алгоритмы настройки гиперпараметров дают одинаковую точность, однако, с ростом размерности стандартный метод обучения модели с ковариационной функции, использующей расстояние Махаланобиса, существенно проигрывает в точности по сравнению с предложенным подходом поворота, координатных осей в связи с ростом числа, гиперпараметров, которые необходимо оценивать в процессе обучения (см. также результаты тестирования на. многомерных данных в [1]).

5.2.    Сравнение точности методов эффективного снижения размерности

В данном разделе протестирована, точность предложенного метода, эффективного снижения размерности в том случае, когда, зависимость, порождающая данные, имеет вид f (x) = g(xBT). (9)

Для иллюстрации качества, решения задачи эффективного снижения размерности с помощью разработанного алгоритма, было проведено сравнение предложенной процедуры с популярными подходами: Sliced Inverse Regression [8,9], Structural Adaptation via Maximum Minimization [19], Minimum Average Variance Estimation [12], Outer Product of Gradients [12], Partial Lest Squares [11].

Точность процедуры определялась близостью пространств, задаваемых настоящей матрицей B и её оценкой B. Мера близости вычислялась согласно формуле Е = || (I — B^TB)B ^TБ\\. Размерность сжатия при этом считалась известной.

Для тестирования использовался набор из 27 гладких функций, которые обычно применяются для тестирования алгоритмов оптимизации [21]. Размер обучающей выборки составлял 300 точек, исходное пространство имело размерность 10. мат puna. B — размер 5 х 10. Для осуществления сжатия генерировалась ортогональная матрица B f _иц размера 10 х 10. Из ее 5 строк составлюгтась матрица B. Далее для фупкщш f в т<>нке x G R¹⁰ значение вычислялось согласно формуле y = f (xB^T ).

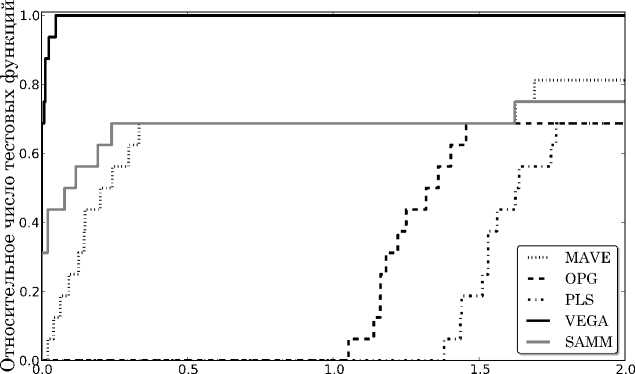
Логарифм расстояния между пространствами

Рис. 3. Кривые Долана. Мора, для набора, тестовых функций по ошибкам сжатия/восстановления

Результаты сравнения (с помощью кривых Долана-Мора, см. [3]) методов приведены на. рис. 3. Предложенная процедура, оказалась наиболее эффективной в сравнении со стандартными подходами.

5.3.    Эксперименты по оценке размерности

В этом разделе рассмотрена, эффективность предложенного метода, оценки размерности в случае выполнения модели (9). Далее приведены результаты вычислительных экспериментов для случая пространства размерности 10 (х € [—1, 1]¹⁰) и случайной ортогональной матрицы В = {/31, ...,/35} размера 5 х 10. В экспериментах использовались следующие искусственные функции:

• •    Сумма квадратов (SqSum): /₁(х) = E5=i г(3іх)².

• •    Функция Griewank: А( х ) = E5=i ⁽⁶⁰⁰§x^{2 -} П5=х cos (600^) + 1.

• •    Функция Trid: /i( x ) = E5=i(Д^ х )² - Е5=1(Д х )(Д-1 х )-

• •    Функция Berm: /1^(x) = (^£L1 [Е5=1⁽^ ^{+ b)} (^ ^- 1)]) .

В таблице 1 приведены оценки размерности для рассмотренных функций в зависимости от размера обучающей выборки.

Таблица!

Результаты оценки размерности с помощью предложенного статистического теста

Function	Sample size
	50 60 70 80 90 100 200 300 400
SqSum Griewank Trid Perm	2    2    7    5    5     5      5      5      5 1    7    7    2    3     5      5      2      5 1    4    8    1    6     5      5      5      5 1     1    7    7    7     6      6      5      5

С ростом выборки оценка, размерности с помощью предложенного статистического теста, постепенно сходится к настоящему значению. Темп сходимости определяется сложностью функции.

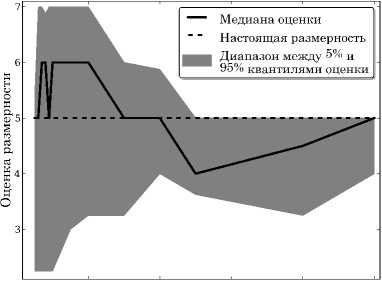
Для функции Trid приведен график, показывающий разброс результатов оценки от размера. выборки (см. рис. 4). Для каждого размера, выборки, рассмотренного в предыдущем тесте (см. таблицу 1), было сгенерировано по 5 случайных наборов данных. По оси ординат отложена разность оцененной размерности и настоящей, то есть значение 0 соответствует правильной оценке размерности. На этом примере видно, что разброс по запускам уменьшается с ростом выборки и оценка сходится к правильному значению. Аналогичный результат для более сложной функции Perm изображен на. рис. 5. В этом случае для рассмотренных размеров выборки не удается получить такую же хорошую картину сходимости, однако в целом с ростом выборки оценка, также постепенно сходится к настоящему значению.

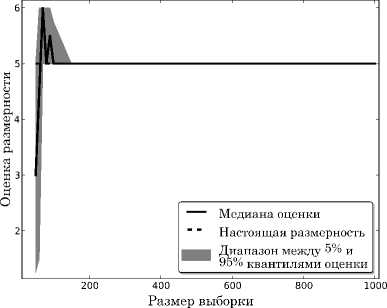
Рис. 4. Оценка размерности на функции Trid для нескольких запусков

200         400         600         800         1000

Размер выборки

Рис. 5. Оценка размерности на функции Perm для нескольких запусков

5.4.    Эксперименты на реальных данных Рис. 6. Ошибка, аппроксимации для задачи предсказания эпергозатратпости маневров вертолета.

Для демонстрации эффективности предложенного подхода, была, рассмотрена, задача, аппроксимации энергозатрат по параметрам маневра вертолета, включающим в себя 51 величину: масса, моменты вращения, углы, высота, и т.п. Были рассмотрены аппроксимации на. основе гауссовских процессов с тремя подходами к подстройке параметров ковариационной функции: 1) стандартный подход с использованием взвешенного евклидова, расстояния; 2) предложенный в статье метод на. основе расстояния Махал ано бис а; 3) пред- ложенный в статье метод в комбинации со снижением размерности на основе выделения направлений с наиболее значимой изменчивостью аппроксимируемой функции. Ошибка аппроксимации оценивалась во всех случаях с помощью десятикратного скользящего контроля. Эффективная размерность данных, оцененная с помощью статистического теста, составила от 12 до 15 параметров в зависимости от номера итерации процесса скользящего контроля. Результаты, приведенные на рис. 6, говорят о целесообразности применения предложенного метода на данной задаче. Более того, сокращение числа параметров в ~ 4 раза на основе выделения наиболее значимых направлений позволяет сохранить качество аппроксимационной модели, существенно сократив сложность задачи.

6.    Вывод

В работе описывается процедура построения регрессии на основе гауссовских процессов, позволяющая осуществить линейное снижение размерности данных. Кроме того, предлагается процедура оценки размерности сжатия данных. Эксперименты показали высокое качество предложенных процедур.

Работа выполнена при поддержке Лаборатории структурных методов анализа данных в предсказательном моделировании МФТИ, грант правительства РФ дог. 11.G34.31.0073.