Выделение малоразмерных объектов алгоритмами сегментации на основе модели системы со случайной скачкообразной структурой

Одной из важных задач обработки изображений является их сегментация. Задача сегментации изображений практически неизбежно возникает при построении различных систем обработки двумерных и трехмерных изображений, систем обнаружения и систем распознавания образов [1]. В большинстве случаев под сегментацией понимают выделение на изображении однородных участков (ОУ). Понятие "однородность участка" определяется условиями задачи, например, однородными могут считаться области с одинаковыми параметрами распределения яркости, одинаковыми параметрами текстуры, типом поверхности и т.д. В данной работе под сегментацией будем понимать разделение локационного изображения подстилающей поверхности на ОУ, соответствующие определенным типам (классам) подстилающей поверхности (например- лес, поле и т.д.) со средним значением на изобра- ( i )

жении величины m ⁽⁾, где 1 -номер класса подстилающей поверхности.

С достаточной для практики точностью подстилающая поверхность может быть представлена совокупностью чередующихся ОУ. При переходе от одного участка к другому значение m ^{( 1} ) меняется произвольным образом, что позволяет рассматривать систему формирования изображения как систему со случайной скачкообразной структурой, генерирующую дискретную последовательность значений яркости элементов изображения (ЭИ). Используя такое представление, на основе обработки изображения производится постановка в соответствие каждому его элементу номера класса подстилающей поверхности 1 . Таким образом, изображение оказывается сегментированным.

В работе [2] на основе модели системы со случайной скачкообразной структурой разработаны алгоритмы, позволяющие эффективно сегментировать изображение подстилающей поверхности, проведено исследование их эффективности при сегментации ОУ, значительно превосходящих по площади размеры элемента разрешения локатора.

Цель данной работы - построение алгоритмов сегментации изображений со сглаживанием достаточной статистики и исследование свойств алгоритмов на основе модели системы со случайной скачкообразной структурой по выделению малоразмерных объектов.

1.    Алгоритмы сегментации со сглаживанием достаточной статистики

Аналогично [2] процесс формирования яркостных отсчетов X k строки изображения опишем моделью одномерной авторегрессии. С учетом обозначений, принятых в [2], процесс смены классов подстилающей поверхности описывается дискретной марковской последовательностью { 9 k , 1 = 0,1,... } , состояния которой 1 являются номерами классов ( 1 = 1,2,..., M ).

Для случая, когда возможно запоминание всей строки изображения X N = { X ₀, X j ,—, X N } , задача состоит в оценивании 9 ₀, 9 ₁,..., 9 N на основе наблюдений X N . Оценку номера класса будем определять по критерию максимума апостериорной вероятности. Сглаженная достаточная статистика удовлетворяет рекуррентному уравнению в обратном направлении отсчетов ( k = N - 1, N - 2,...0) [3]:

W k,N ( 9 k = в ) = W k ( 9 k = в ) £^----- p ^{Xk + 1 I X}k ’ ^{9 + 1} j ’ ^{9Wk + 1} j ^{9 в} ------W k _{+ 1} N ( 9 k + 1 = j )     ⁽¹⁾

j = ¹ E p ( X k + 1 I X k , 9 k + , = j , 9 k = 1 П9 . . = j 9 = 1 )W k ( 9 k = 1 )

1 = 1

с начальным условием:

Wn,N (9n ) = Wn (9n ), где Wk N (9k = в) = P(9k = вХ ) - сглаженная апостериорная вероятность принадлежности k-го ЭИ к в-му классу (в = 1,2,...,M); Wk(9k = в) =

P(9k = pIXX) - апостериорная вероятность принадлежности к-го ЭИ к в -му классу, полученная при обработке строки изображения в прямом направлении отсчетов [2]; p(Xk+1X,9k+1,9k), n(9k) -условные плотности вероятности и переходные вероятности соответственно. Алгоритм сегментации, определяемый выражением (1), назовем одностроч- ным алгоритмом сегментации со сглаживанием достаточной статистики – сокращенно ОА2 в отличие от однострочного алгоритма, представленного в работе [2], который сокращенно назовем ОА1.

При обработке изображения по строке и столбцу в соответствии с выражением (1) путем усреднения соответствующих апостериорных вероятностей получим комбинированный алгоритм сегментации со сглаживанием достаточной статистики, назовем его КОА2. Комбинированный алгоритм сегментации, полученный в работе [2], назовем КОА1.

2.    Выделение алгоритмами сегментации малоразмерных объектов

Под малоразмерными объектами будем понимать ОУ, сравнимые по площади с размерами элемента разрешения локатора.

Для исследования свойств алгоритмов сегментации изображений на основе модели системы со случайной скачкообразной структурой по выделению малоразмерных объектов была проведена серия тестовых экспериментов методом имитационного моделирования для двух классов подстилающей поверхности ( М =2). Первый класс подстилающей поверхности соответствует фону, второй класс – малоразмерным объектам с соответствующими средними уровнями яркостей m ⁽¹⁾ и m ⁽²⁾ . В качестве модели изображения выбиралось тестовое поле размером 150х150 ЭИ, представленное совокупностью ОУ фона и объектов, сформированных в соответствии с выражением (4) в [2]. Параметры моделей определялись следующим образом: m (1) = m 0 = 150; m (2) = m ₀ + A m ; p Xy2 = 0,1; ^(1,2) = 2. Ошибка в определении номера класса, аналогично [2], оценивалась значением P ОШ , называемой ошибкой распознавания состояния:

1 NL

^Р ош =^" Z^ zi , k , ⁽²⁾ NL k = 1 I = 1

где L , N – размеры изображения по вертикали и горизонтали, z_l,k – величина, принимающая значение ноль в случае, когда оценка номера класса O _lk и номер класса θ l,k l,k -го ЭИ совпадают, и равная единице в противном случае.

Свойства подстилающей поверхности определяются элементами матрицы переходных вероятностей (МПВ):

п ( O k +W ) =

^п 11

.^п 21

^п 12

^п 22

Для описания результатов исследований введем коэффициенты К 12 и К 22 , определяемые МПВ (3):

К - ^П 21 ■       К - ^П 22 v ^П 12

K 12 =---- ^;       K 22 =---- ^х----.              ⁽⁴⁾

^п 22                ^п 21 ^п 11

Значение К12 увеличивается при росте числа объектов на изображении и уменьшении их размеров. В процессе исследований линейные размеры объектов изменялись от 49х49 ЭИ до 3х3 ЭИ. Коэффициент К22 характеризует соотношение площади объектов и фона на изображении. С целью детального исследования свойств алгоритмов ошибка распознавания состояния рассчитывалась как по всему изображению (ALL IMAGE), так и по площади выделяемых объектов (OBJECT).

Сначала исследовалась зависимость P ОШ от К 12 при фиксированных значениях К 22 . Графики зависимости представлены на рис. 1, 2 для К 22 =0,1 и К 22 =0,01, при которых площадь объектов составляет 10% и 1% от площади фона на изображении соответственно. Из графиков видно, что с увеличением К 12 , то есть с увеличением числа объектов и уменьшением их размеров, ошибка распознавания растет. При этом ошибка по всему изображению больше в том случае, когда больше площадь объектов на изображении. Ошибка по площади объектов больше при меньшем значении К ₂₂. Такое поведение кривых на графиках объясняется влиянием МПВ (3) на работу алгоритмов. Наиболее эффективны алгоритмы сегментации со сглаживанием достаточной статистики ОА2 и КОА2. Как видно из графиков, при малых размерах объектов ( К 12 =0,5) эффективность алгоритмов сегментации становится низкой – P ОШ достигает значений более 0,5. Поэтому размеры сегментируемых участков объектов не могут быть менее 5x5 ЭИ.

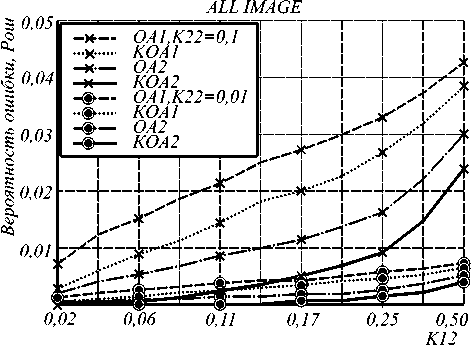
Рис.1. Зависимость ошибки распознавания состояния по всему изображению от коэффициента К12

Далее проводилось исследование зависимости P_ОШ от К ₂₂. Графики зависимости представлены на рис. 3, 4 для К 12 =0,02 и К 12 =0,5. Из графика на рис. 3 видно, что при увеличении соотношения площади объектов и фона на изображении P ОШ по всему изображению увеличивается, а по площади объектов уменьшается (рис. 4). При этом при достаточно больших значениях К 12 ( К 12 =0,5) ошибка имеет значения более 0,5. Таким образом, удовлетворительная работа алгоритмов сегментации возможна при ограничении размеров сегментируемых участков объектов.

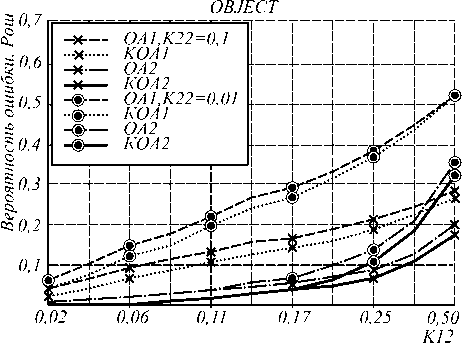
Рис.2. Зависимость ошибки распознавания состояния по площади объектов от коэффициента К12

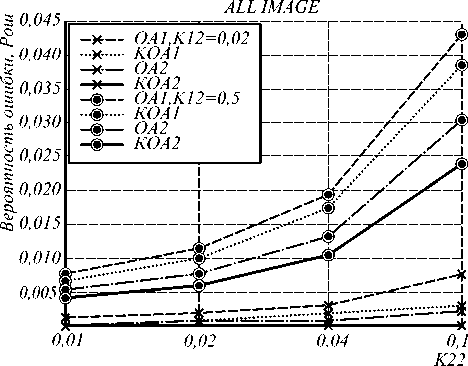
Рис.3. Зависимость ошибки распознавания состояния по всему изображению от коэффициента К22

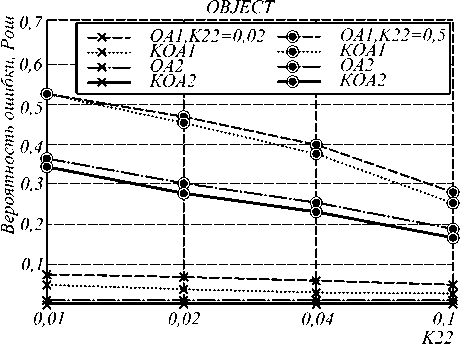
Рис.4. Зависимость ошибки распознавания состояния по площади объектов от коэффициента К22

Следующие графики отражают зависимость

PОШ (рис. 5, 6, 7, 8) от параметра ∆m , равного разности средних уровней яркостей классов объектов и фона. Из рис. 5,6,7,8 видно, что с увеличением ∆m ошибка уменьшается, причем при ∆m = 10 - 15 уменьшается до нуля в зависимости от применяемого алгоритма. При увеличении соотношения площади объектов и фона на изображении при фиксированных значениях К12 (рис. 5) ошибка распознавания по всему изображению увеличивается, а по площади объектов – уменьшается. Как отмечалось выше, это объясняется влиянием МПВ (3) на работу алгоритмов. При уменьшении размеров объектов и увеличении их числа (с увеличением К12) при фиксированных значениях К22 ошибка распознавания состояния увеличивается, достигая больших значений по площади объектов (рис. 7, 8). Из сравнения графиков, приведенных на рис. 5, 6 и 7, 8, следует, что эффективность сегментации изображений в большей степени определяется размерами и числом объектов на изображении, чем соотношением площади объектов и фона.

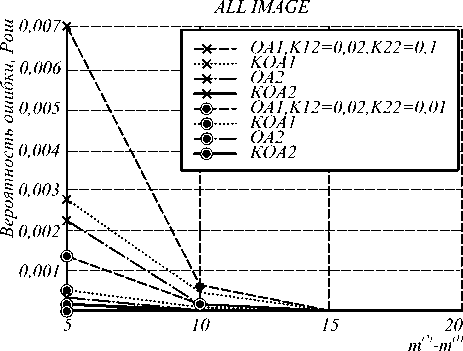
Рис.5. Зависимость ошибки распознавания состояния по всему изображению от ∆ m при К₁₂=Const

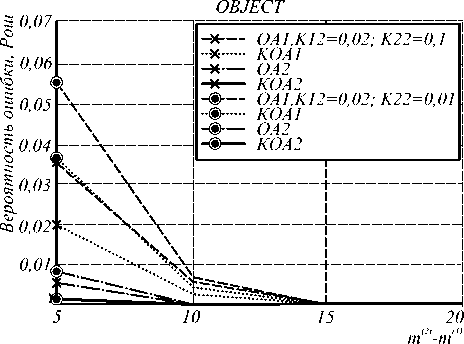
Рис.6. Зависимость ошибки распознавания состояния по площади объектов от ∆ m при К₁₂=Const

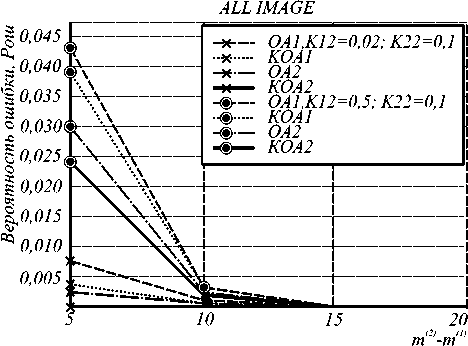
Рис.7. Зависимость ошибки распознавания состояния по всему изображению от A m при К₂₂=Const

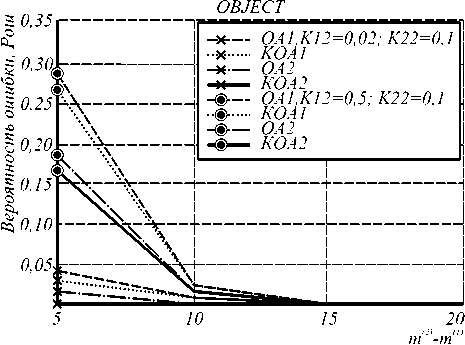
Рис.8. Зависимость ошибки распознавания состояния по площади объектов от A m при К₂₂=Const

Для иллюстрации работоспособности рассмотренных алгоритмов ниже приведен пример обработки реального изображения городской застройки, полученного когерентным локатором и представленного на рис. 9, с помощью алгоритма сегментации КОА2 (рис. 10) при следующих условиях: М =3; m ⁽¹⁾ = 54, m ⁽²⁾ = 99, m ⁽³⁾ = 197; р '^ ^;' = 0,1; _a ⁽¹⁾ = 14, <т ⁽²⁾ = 30 , □ ⁽³⁾ = 51. Из рисунков видно, что на обработанном изображении малоразмерные объекты, соответствующие типу подстилающей поверхности с m ⁽³⁾ = 197, выделены с сохранением их границ.

Заключение

Результаты исследования свойств алгоритмов сегментации изображений, разработанных на основе модели системы со случайной скачкообразной структурой, показывают возможность эффективного выделения малоразмерных объектов на изображении.

Наиболее высокой эффективностью обладает комбинированный алгоритм сегментации со сглаживанием достаточной статистики. Полученные характеристики эффективности алгоритмов позволяют определить ограничения на размеры сегментируемых участков объектов.

Рис.9. Реальное изображение когерентного локатора

Рис.10. Обработанное алгоритмом сегментации КОА2 изображение

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант РФФИ № 06-08-00596-а.