Выделение сигналов из их смеси (элементы алгоритмов и нейросетевых структур)

Задачи восстановления формы сигналов (ВФС), регистрируемых средствами нескольких каналов в виде смеси с различными соотношениями, имеет значительное количество приложений, поскольку чаще всего первичный информационно значимый вектор-сигнал (т. е. группа сигналов по нескольким каналам) не является доступным в используемой системе измерений. В частности, в системах беспроводной связи методы уплотнения каналов с временным или частотным разделением используют наиболее простой вид ВФС, когда компоненты смеси занимают ненакладывающиеся интервалы в частотной или временнóй области. При перекрытии спектров компонент неполное ВФС возможно только при частичном их наложении в об- ласти время-частотных преобразований. Среди потенциальных приложений ВФС — обработка многокомпонентных речевых сигналов, геофизических данных, анализ многоканальных биомедицинских сигналов (ЭЭГ, ЭМГ, ЭКГ) и анализ сигналов элементов антенны при приеме множественных целей.

Возможные формы постановки задачи ВФС, включают ряд вариантов.

– Выделение группы сигналов-компонент, определяющих максимальную долю дисперсии регистрируемых смесей сигналов источника (СИ)

• -    ВФС по критерию независимости ее компонент.

• -    ВФС без информации о виде и количестве компонент и пропорциях их в смесях.

  

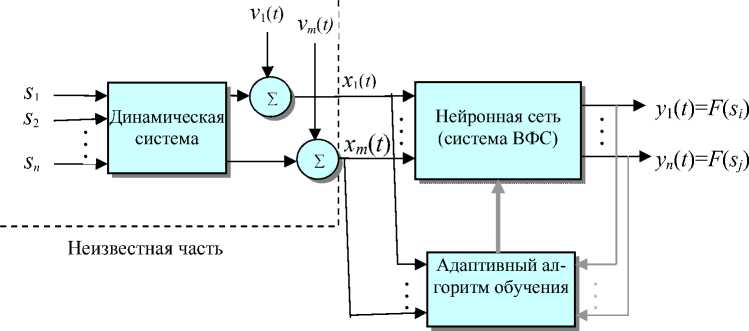
  Рис. 1. Блок-схема обработки сигналов для восстановления их формы по данным регистрации смеси на выходе линейной динамической системы

  
  

Общая постановка задачи ВФС предполагает, что наблюдаемый m -компонентный вектор-сигнал x ( t ) = [ x ₁( t ), x ₂( t ),..., x_m ( t )]^T регистрируется нелинейной динамической системой, имеющей n входов и m выходов. Целью является получение обратной системы (в виде нейронной сети или другой адаптивной структуры), оценивающей первичный вектор-сигнал s ( t ) = [ s ₁( t ), s ₂( t ),..., s_n ( t )]^T , поступающий на сенсоры. Оценка s ( t ) осуществляется на основе n -мерного вектора-сигнала y ( t ) = [ y ₁( t ), y ₂( t ),..., y_n ( t )]^T на выходе обратной системы (рис. 1). Предпочтительно, чтобы обратная система была адаптивной, т. е. могла отслеживать нестационарные изменения s ( t ) и, следовательно, поступающего на ее вход сигнала x ( t ) .

Иногда вместо прямой оценки СИ более удобно сначала идентифицировать систему, смешивающую сигналы, или фильтрующую динамическую систему. Это бывает, когда обратную систему трудно получить или когда количество смесей меньше, чем число первичных СИ.

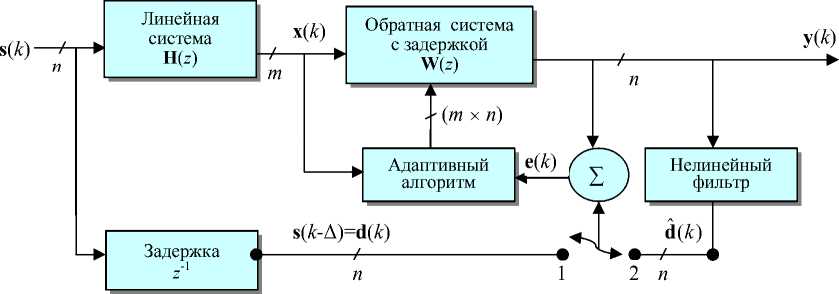
Задача ВФС отличается от задачи полной обратной идентификации СИ. При идентификации (с помощью обратной системы) требуется получить доступ к первичным СИ, т. е. оценить задержанные (возможно, сглаженные) выходы обратной системы (ОС) на основе минимизации среднеквадратичного различия (ошибки) между задержанными СИ и сигналами выхода ОС. Модель системы для задачи обратной идентификации показана на рис. 2, а, а основанное на модели адаптивное обратное управление — на рис. 2, б.

а

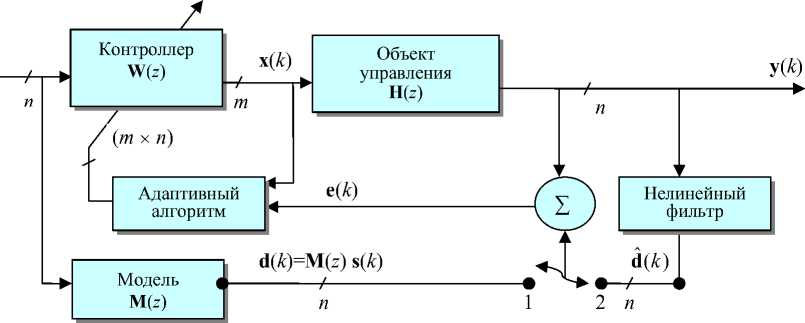
Рис. 2. Структура системы для задачи обратной идентификации (а) и адаптивная структура "обратного" управления (б), которое основано на модели. При переключателе в положении 1 реализуется адаптивная обратная система (путем минимизации ошибки e ); при положении 2 — оценивается ошибка e

б

В задаче адаптивного обратного управления выбирается вид адаптивного контроллера, передаточная функция которого является обратной по отношению к объекту управления (ОУ). Такая адаптивная система обеспечивает следование ОУ за входными сигналами-командами, т. е. за сигналами источника. При этом вектор-сигнал ошибки e ( k ), определяемый разницей между выходом ОУ и (опорным) сигналом модели, используется в обучающем адаптивном алгоритме для подстройки параметров линейного контроллера (рис. 2, б). Считается желательным, чтобы выход ОУ отслеживал не сами СИ, а задержанные или сглаженные (фильтрованные) входные сигналы d ( k ), получающиеся после преобразования М ( z ) [1, 2]. Такая структура с последовательным включением контроллера и ОУ после завершения адаптивной подстройки (процесса обучения) начинает моделировать динамику выходного сигнала по опорной модели М ( z ).

ЭЛЕМЕНТЫ ОБЩЕЙ КОНЦЕПЦИИ РАЗДЕЛЕНИЯ СИГНАЛОВ СМЕСИ

Решение задачи ВФС базируется на методе анализа главных компонент [3–5] и на более новых подходах к разделению сигналов, таких как последовательное извлечение СИ из смеси на выходе системы с преобразованием типа свертки [5– 7]. В зависимости от особенностей приложения задачи ВФС процессы смешивания и фильтрации неизвестных СИ могут соответствовать различным математическим или физическим моделям.

В наиболее простом случае m смешанных сигналов x i (k ) ( i = 1,2,..., m ) являются линейной комбинацией n ( n <  m ) неизвестных, статистически взаимно независимых СИ s i ( k )( i = 1,2,..., n ), которые имеют нулевые средние и "искажены" присутствием сопутствующего шума. Этот случай описывается соотношением (1) или его матричной формой (2):

n

x ⁽ k ) = Ё h j s j ^{( k} ) + ^v i^{( k} ) ⁽¹ = ¹ , ² ,-, ^m ),     ⁽¹⁾

j = 1

x ( k ) = H • s ( k ) + v ( k ),                         (2)

где

x ( k ) = [ x 1 ( k ), x ₂ ( k ),..., x_m ( k )] T — вектор сигналов сенсоров;

s ( k ) = [ S i ( k ), s 2 ( k ),..., s n ( k )] T — вектор СИ;

v ( k ) = [ v 1 ( k ), v ₂( k ),..., v_m ( k )] T — вектор аддитивного шума;

H — неизвестная смешивающая матрица размера m x n и полного ранга (т. е. ранг матрицы H равен n )¹.

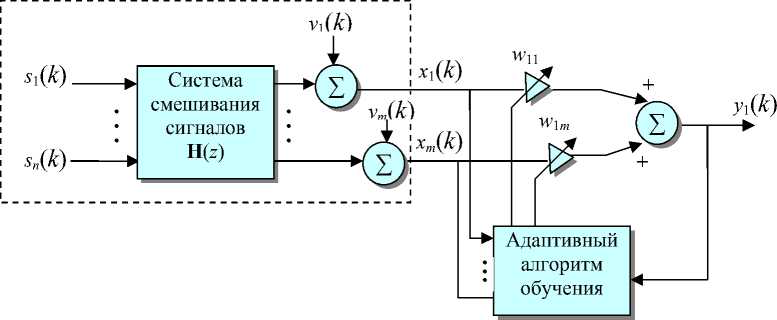
Чаще всего предполагается, что количество СИ n неизвестно, доступным является только вектор-сигнал сенсоров x ( k ) ; требуется использовать нейронную сеть с прямым распространением (или рекуррентную сеть) и адаптивный алгоритм обучения, позволяющий оценить СИ, идентифицировать смешивающую матрицу H или разделяющую матрицу W [8, 9] (рис. 3). При этом достигается достаточно хорошая адаптация значений получаемых матриц H и W к изменениям СИ.

Задача ВФС может трактоваться как анализ независимых компонент. При этом для разделения вектора-сигнала x ( k ) = [ x 1 ( k ), x ₂( k ),..., x_n ( k )] T и восстановления формы первичных сигналов (СИ) требуется найти линейное преобразование в виде "разделяющей" матрицы W размерности n x m , полного ранга и такой, чтобы выходной вектор-сигнал y ( k ) = [ У 1 (k ), y ₂( k ),..., y_n ( k )] T , определенный соотношением y = W x , содержал компоненты, которые максимально статистически независимы. Степень независимости компонент проверяется с помощью информационно-теоретического критерия Кульбака—Лейблера [12], [13]. При таком подходе к задаче ВФС требуется адаптация весов w ij — компонент матрицы W линейной системы y = W x , которая реализуется в виде однослойной нейронной сети. Эта сеть комбинирует наблюдаемые и измеряемые x i ( k ) и дает оценку s ˆ _j ( k ) СИ:

m sj(k)=yj(k)=Ewjx^k), (j=1,2,...,n)• (3) i=1

Оптимальные веса соответствуют статистической независимости выходных сигналов y_j ( k ) (рис. 3, б).

Концепция и типы формализации задачи ВФС, приспособленные к особенностям приложений, строятся с использованием ряда модификаций метода анализа независимых компонент.

МОДИФИКАЦИИ МЕТОДА АНАЛИЗА НЕЗАВИСИМЫХ КОМПОНЕНТ

Применение метода АНК для получения оценок сигналов, регистрируемых в виде их смеси, имеет некоторые особенности, связанные со спецификой приложений.

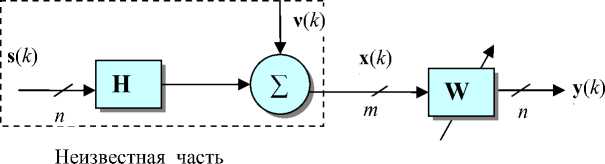
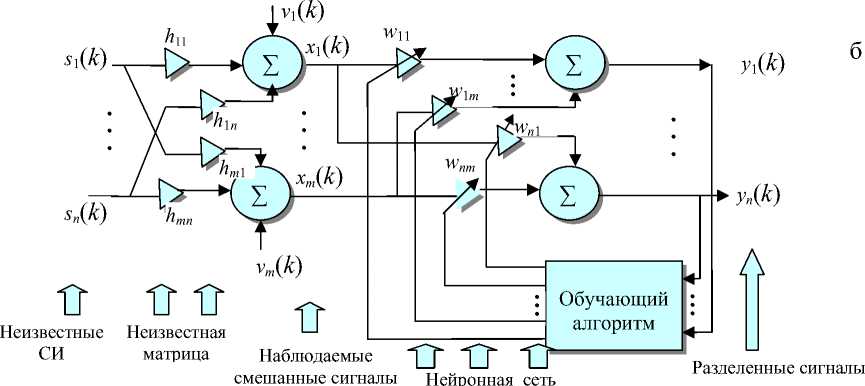
Рис. 3. Векторно-матричная структура (а) и логика (б) системы разделения сигналов (ВФС)

• ■    При АНК зашумленного стохастического ( m -мерного) сигнала x ( k ) определяется разделяющая матрица W размера n х m ( n <  m ), которая по соотношению y = W·x дает вектор-сигнал y ( k ) = [ У 1 (k ), У 2 ( k ),..., y n ( k )] T , содержащий оценку компонент СИ s ( k ) e R n , причем эти компоненты "насколько возможно" статистически независимы. Как отмечено выше, степень независимости контролируется по критерию Кульбака—Лейблера.

• ■    Для зашумленного вектора-сигнала x ( k ), определяемого выражением x ( k ) = H·s ( k ) + ν ( k ) (где H — смешивающая ( m х n ) -матрица; s ( k ) = = [ s 1 ( k ), s ₂( k ),..., s_n ( k )]^T— вектор СИ со статистически независимыми компонентами; ν ( k ) = = [ ν 1 ( k ), ν 2 ( k ),..., ν m ( k )]^T — вектор некоррелированных компонент шума) метод АНК реализуется путем оценивания как смешивающей матрицы H , так и независимых компонент s ( k ) = = [ S i ( k ), s 2 ( k ),..., s n ( k )]^T.

• ■    АНК может формулироваться как задача оценки всех СИ, количества СИ и (или) идентификации смешивающей матрицы H или псевдо-обратной разделяющей матрицы W = H ⁺ . При этом единственным допущением является стати-

• стическая независимость первичных СИ и линейная независимость столбцов матрицы H. (Последнее допущение равноценно тому, что ранг H равен n). В контексте метода АНК модель смешивания СИ, объединяющая набор (из N) векторов-сигналов X = [x(1),x(2),...,x(N)]T eRmхN и соответствующий набор N сигналов источника S = [s(1),s(2),...,s(N)]T eRnхN, может быть представлена в виде:

X = H • S . (4)

В приложениях, где при большом количестве независимых компонент, имеющих "разреженное" распределение (со значительным относительным взаимным расстоянием друг от друга), используется зависимость (эквивалентная (4))

X T = S T ■ H ^T. (5)

Операция транспонирования изменяет роли матрицы H = [h1,h2,...,hn]T и матрицы независимых компонент (матрицы СИ) S = [s(1),s(2),...,s(N)]T. Поэтому векторы-столбцы матрицы HT могут рассматриваться как независимые компоненты, а матрица ST — как матрица смешивания (и наоборот, как в (4)). В обычной временнóй модели АНК принимается, что независимые компоненты s(k) являются временными сигналами, а матрица смешивания является фиксированной матрицей без наложения каких-либо ограничений на ее элементы. В пространственно-временнóй модели АНК различие между главными компонентами и матрицей смешивания полностью перестает существовать, т. е. делаются одинаковые или подобные предположения относительно главных компонент и относительно матрицы смешивания [5, 14].

• ■    В отличие от обычного метода АНК при использовании пространственно-временнóго АНК производится максимизация степени независимости по времени и пространству выборок X и S . Для этой модели АНК вероятностная матрица X ( X T = S T • H T ) получается оцениванием обоих неизвестных матриц: S и H. И делается это таким путем, чтобы строки у матрицы S и столбцы у матрицы H были независимыми и чтобы S и H обладали одинаковыми или подобными статистическими свойствами (например, распределением Лапласа или разреженным распределением главных компонент).

• ■    В реальных приложениях данные на сенсорах представляют сложные нелинейные структуры из компонент СИ, поэтому применение АНК ко всей совокупности данных может привести к неудовлетворительным результатам. Вместо применения АНК ко всей совокупности данных оказывается полезной предварительная их обработка с группировкой в кластеры или в подгруппы, однородные по особенностям данных. После этого АНК применяется последовательно (индивидуально) к каждому кластеру или подгруппе.

Стадия предобработки с подходящей группировкой или кластеризацией данных особенно разумна для случая значительной нелинейности в представлении данных на сенсорах. В то же время линейная модель АНК отдельных кластеров используется для описания локальных свойств данных. В локальной модели АНК для непосредственно измеряемых данных с сенсоров производится предварительная обработка, например преобразование (фильтрация) их с помощью согласованного многоканального разделения (СМР) [2], применения вейвлет-преобразования, совместного время-частотного анализа. Затем производится кластеризация в пространственной, частотной или время-частотной областях, после чего применяется линейная форма АНК в отдельности (локально) в каждом кластере или в частотном диапазоне. Таким образом, оптимальный локальный АНК может быть выполнен как результат совместного взаимодействия двух процессов: подходящего процесса кластеризации и процесса АНК в применении к каждому кластеру.

• ■    В приложениях, связанных с задачами ВФС, иногда бывает необходимо оценить только одну или несколько желаемых компонент (вектора СИ), которые обладают особыми статистическими признаками или свойствами, и не рассматривать остальные компоненты и шумы (информативно незначимые для этого приложения). В этом случае используется метод (близкий к модификации АНК), условно называемый извлечением сигналов с восстановлением их вида (ИСВВ).

ИСВВ формулируется как задача оценки одного или отобранного числа СИ с желаемыми свойствами или характеристиками, причем извлечение и оценка вида выбранных сигналов производится последовательно один за другим. Эквивалентная формулировка задачи ИСВВ такова. Необходимо идентифицировать соответствующий вектор (или векторы) h j матрицы смешивания H и их псевдо-обратные w j , являющиеся строками разделяющей матрицы W = H ⁺ . При этом предполагается независимость компонент первичного вектора-сигнала источника и линейная независимость столбцов матрицы H .

ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ ПО КОНЦЕПЦИИ РАЗДЕЛЕНИЯ СИГНАЛОВ СМЕСИ

Можно сказать, что пока нет сформировавшейся методологии в области прикладных задач, связанных с ВФС или ИСВВ по измерительным данным об их смеси, особенно при большой размерности вектор-сигналов и при нелинейном типе смешивания. Встречается подмена понятий ВФС, АНК и ИСВВ, хотя они относятся к одной и той же или очень близкой проблематике современных алгоритмов обработки сложных и нелинейных комбинаций многомерных сигналов при предположении статистической независимости их компонент. Однако в реальных задачах использование АНК и ВФС направлено на несколько различающиеся цели.

• ■    Целью ВФС служит получение оценки СИ, даже если они не полностью взаимно статистически независимы, в то время как цель АНК состоит в определении такого преобразования, которое обеспечивает, чтобы выходные сигналы были (максимально) статистически независимыми.

• ■    Методы АНК, как правило, основаны на использовании статистик высокого порядка (кумулянт), а в базовом методе ВФС используются только статистики второго порядка (СВП). Метод на основе СВП предполагает, что СИ имеют некоторую временнýю структуру, в то время как использование статистик высокого порядка предполагает их полную статистическую независимость. Второе различие состоит в том, что метод,

  

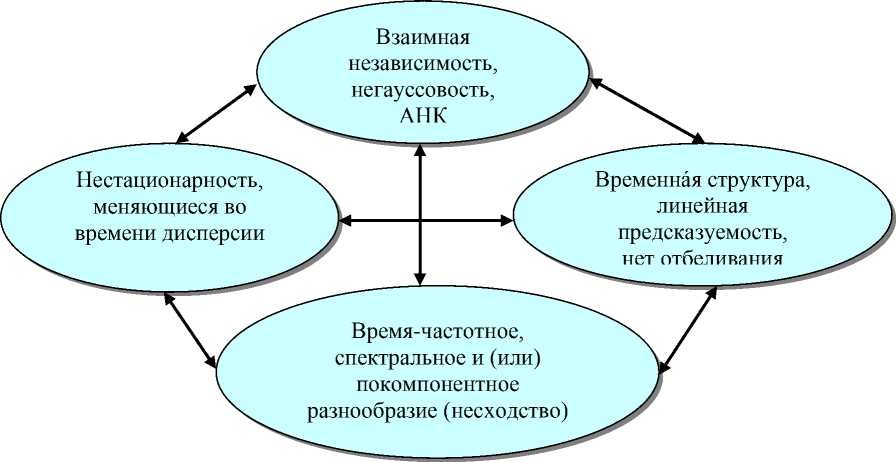
  Рис. 4. Элементы априорных знаний как основа формирования алгоритмов для задач разделения сигналов по измерениям их смеси

  
  

основанный на статистиках высокого порядка, не может быть применен к гауссовым сигналам (т. е. при нормальном распределении компонент СИ), а метод, основанный на СВП, не имеет такого ограничения. Фактически методы ВФС (в описанной выше их интерпретации) не замещают АНК, и наоборот, т. к. каждый подход основан на различных предположениях и часто на различных целевых установках.

Основные подходы к формированию алгоритмов разделения смеси СИ неявно связаны с априорными представлениями и знаниями, которые отражены на рис. 4.

• ■    Наиболее часто встречается подход, использующий в качестве критерия меру независимости сигналов (компонент СИ), негауссовость или разреженное распределение главных компонент. Когда компоненты СИ принимаются статистически независимыми и без временнóй структуры, то для решения задачи разделения СИ существенно применяются статистики высокого порядка (неявно или явно). В этом случае допустимо не более одной компоненты и с гауссовым распределением.

• ■    Если СИ имеют временную структуру, то каждая компонента СИ имеет неисчезающие временные корреляции. Это менее ограничивающее условие, чем статистическая независимость. СВП достаточны для оценки смешивающей матрицы и СИ. В этом направлении разработано несколько методов [15–17]. Но все же методы СВП не позво-

• ляют разделять СИ с одинаковым (идентичным) спектром мощности или независимые и одинаково распределенные СИ.

• ■    Третий подход использует свойство неста-ционарности и статистики второго порядка.² В отличие от других подходов метод, основанный на использовании свойства нестационарности, позволяет разделять окрашенные гауссовы сигналы, имеющие идентичную форму частотного спектра мощности. В то же время этот метод не допускает возможности разделения сигналов (ВФС), если сигналы имеют идентичную форму нестационар-ности [19, 20].

• ■    Четвертый подход использует меру различия сигналов. Эта мера оценивается на основе их свойств и характеристик: временных, частотных (спектральных), время-частотных или простран-ственно-время-частотных [21].³

  Желаемый сигнал s ( k )

  Основной сенсор

  

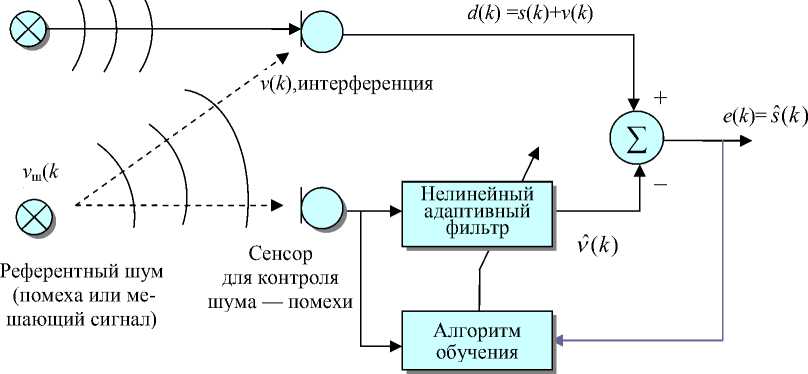
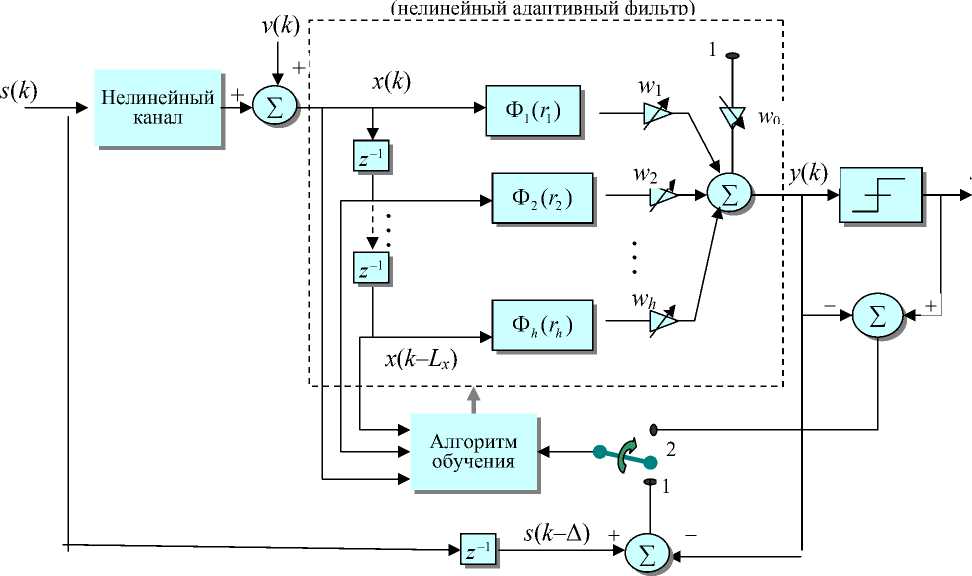
  Рис. 5. Структурная схема для удаления шума при одном канале связи с использованием нелинейного адаптивного фильтра или нейронной сети

  
  

ИСПОЛЬЗОВАНИЕ МЕТОДА АНК ДЛЯ ЗАШУМЛЕННЫХ ДАННЫХ

В присутствии шума оценки разделяющей матрицы W , восстанавливающей форму СИ, и матрицы смешивания H достигаются более сложными процедурами, чем в случае отсутствия шума или при его несущественной значимости. Методическая схема, пригодная для ВФС по зашумленным данным, должна ориентироваться на алгоритмы, робастные к шуму ("устойчивые" или мало зависимые от шума) или на алгоритмы, которые могут обеспечить снижение уровня шума в оценке выходного вектор-сигнала y ( k ).

Естественным предположением является независимость сигнала и аддитивного шума. В отдельных приложениях оказывается возможным интерпретировать шум как неизвестный СИ, и поле (или вектор) шума, поступающее на сенсоры, можно рассматривать как эквивалент дополнительных СИ. Однако при этом для ВФС не более чем одна компонента шума может иметь гауссово распределение, а остальные — негауссово. В отдельных случаях нет необходимости в разделении сигналов шума и восстановлении их вида.

В общем случае решение задачи удаления шума крайне трудна или даже нереализуема, т. к. получается ( m + n ) неизвестных СИ ( n источников и m сигналов шума).

Для удаления шума (безотносительно к многоканальной задаче ВФС по информации об их сме- си) разработан ряд методов [22–24]. С некоторыми модификациями они могут быть использованы для выработки подходов к удалению шума при разделении и ВФС.

В прикладных системах нередко возможно измерить или моделировать шум среды, в которой анализируются информационные сигналы. В этом случае шум называют опорным или референтным (он обозначен ν _ш ( k ) на рис. 5).⁴ Шум ν _п (за счет среды его распространения) может влиять на каждый сенсор неизвестным образом: возможны эффекты задержки, реверберации, эха и нелинейных искажений. Можно считать, что перед тем, как достигнуть сенсора, референтный шум обрабатывается неизвестной динамической системой. В простом случае система преобразования может описываться операцией свертки, где ν _ш обрабатывается некоторым КИХ-фильтром (рис. 6). В этом случае одновременно происходят два процесса обучения: процедура несупервизорного обучения ("без учителя"), осуществляющая разделение сигналов, и супервизорная ("с учителем")

Неизвестная часть

ν _ш ( k ) Референтный шум

H 1 ( z )

W 1 ( z )

s 1 ( k )        ^{h 11}

s 2 ( k )

.

.

.

s n ( k )

h 12

h

H 2 ( z )

H n ( z )

h nn h2n

h

x 1 ( k )

x 2 ( k )

.

.

.

x n ( k )

w 12

w1n w21

w 11

W 2 ( z )

y 1 ( k )

w 22

------* ∑ w2n

y 2 ( k )

w n 1

W n ( z )

w n 2

w nn

.

.

.

y n ( k )

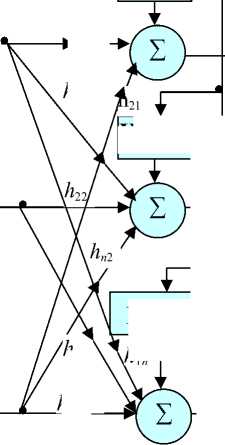
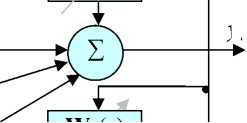
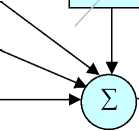
Рис. 6. Структура преобразований, обеспечивающая подавление шума и разделение сигналов при их линейном преобразовании в форме свертки

g _p =∑ _k [ w _k ⋅ h _{p - k} ]

а

б

Неизвестная часть системы

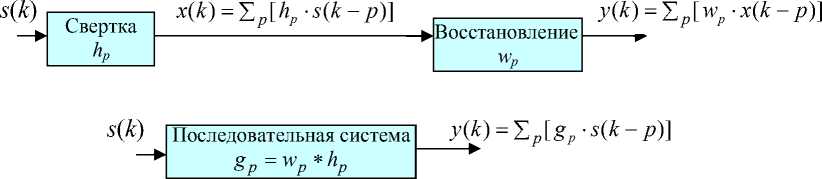
Рис. 7. Схема процедур, связанных с восстановлением сигнала при его преобразовании в виде свертки: одноканальный (а, б) и многоканальный (в) случаи

в

процедура, реализующая алгоритм снижения шу- Каспрзак, Пежунен (Karhunen, Cichocki, Kasprzak, ма. Этот подход использовали Карунен, Сичоки, Pejunen) [25] и Сичоки, Карунен, Каспрзак, Вига-

рио (Vigario) [26] для снижения шума в предположении, что референтный шум доступен для оценки.

РАЗДЕЛЕНИЕ СИГНАЛОВ МНОГОКАНАЛЬНОЙ СМЕСИ В ФОРМЕ СВЕРТКИ

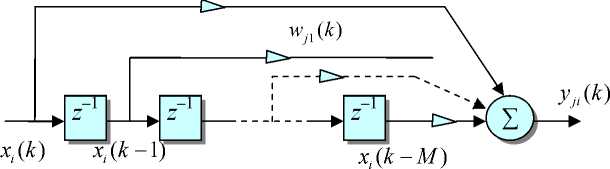
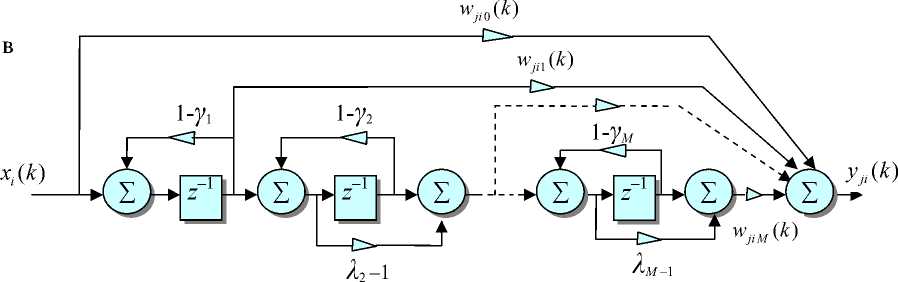
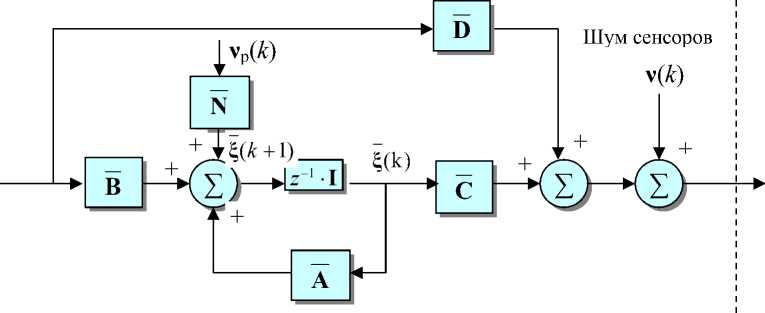
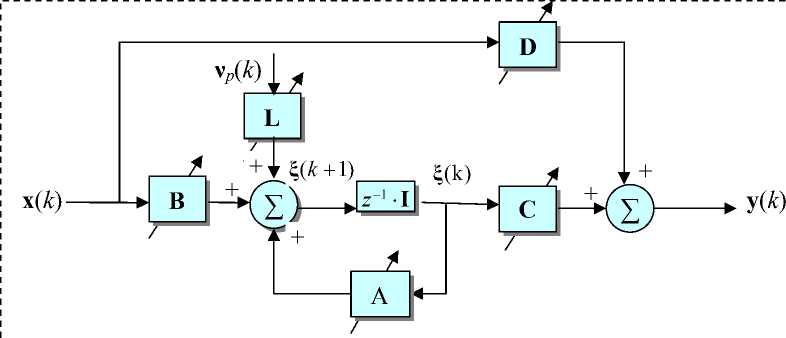
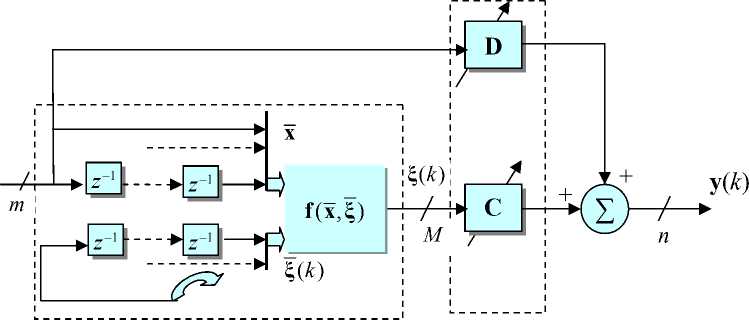
Структурная схема процедур, связанных с восстановлением сигнала при его преобразовании в форме свертки показана на рис. 7, а, б, для одноканального случая (два эквивалентных вида схемы) и рис. 7, в — для многоканальной смеси компонент вектор-сигнала. В многоканальном случае измеряемый сигнал x(k) = [x1(k),x2(k),...,xm(k)]T образуется как смесь типа свертки из компонент n-мерного вектор-сигнала s(k) =[s1(k),52(k)..,sn(k)]T (m > n). Это отражает устойчивая модель to

x ⁽ k ) = E ^H p ^{s ( k} - p ) = ^H p * ^{s ( k} )

p=-to to при EIIHp||

Если определить H(z) соотношением to

H(z) =E Hp • z-^p ,                    (8)

p=-to где z –1 означает операцию задержки на единицу времени (т. е. сдвиг временнóго сигнала назад z –p[si(k)] = si(k – p)), то при замене z на комплексную переменную z = exp(-^ + JroT) H(z) является Z-преобразованием {Hp} — матрицей передаточных функций системы.

Объединение (7) и (8) дает (9):

x( k) =[H( z)] • s( k).                 (9)

Задача разделения сигналов многоканальной свертки состоит в определении (возможно, масштабированных и задержанных) СИ с использованием приблизительных знаний о распределении СИ, их статистических свойствах. Предполагается, что каждый СИ si(k) является независимо и одинаково распределенной последовательностью (по k), которая статистически независима от всех других последовательностей компонент СИ.

Для восстановления СИ могут быть использованы модели нейронных сетей (НС), показанных на рис. 3, б, и рис. 6, но для свободных параметров сети (весов wij) необходимо некоторое обобщение, такое, чтобы НС имела свойство КИХ- или БИХ- фильтра.5 Задача разделения сигналов из смеси, где каждый вес НС (элемент матрицы W ) задается в виде его Z-преобразования

M

Wj,( z, k) = E Wjp (k) • z -^p,           (10)

p=0

описывается многоканальным адаптивным фильтром с конечной импульсной характеристикой и дискретным временем (k). СИ оцениваются с помощью устойчивой модели НС, которая описывается соотношением (11) и показана на рис. 8, а:

toto

• Уз^(k)=EEз^х.(k-p), j=¹,²,-,n.     ⁽¹¹⁾

l=1 p=-to

В матричной форме (11) имеет вид (12):

to

y⁽k) = E Wp^(k) •^{x(k -}p) = Wp^(k) *^x(k)= p=-to

• = [W( z, k)] • x( k),                          ⁽¹²⁾

где y( k) = [ y1( k), y 2( k),., Уп (k )]T — n-мерный вектор на выходе системы; W( k) = {Wp (k)} (-to < p < to) — последовательность n x m коэффициентов матриц, используемых для времени k; матричная передаточная функция (в форме Z-преобразования) определяется выражением to

W(z, k) = E Wp (k) • z-^p. p=-to

Цель адаптивного разделения СИ из смеси в форме свертки достигается подстройкой матрицы W(z, k) таким образом, чтобы общая система (последовательность матриц смешивания H(z) и восстановления W(z, k)) представляла СИ, преобразованные перестановкой компонент (P) и масштабированием (D(z))⁶:

limG(z, k) = W(z, k) • H(z) = P • D(z).     (13)

k ^to

Два типа НС для ВФС с весами в форме БИХ-фильтров с устойчивой ограниченной по величине импульсной характеристикой показаны на рис. 8, б, и рис. 8, в. В обеих структурах, представленных на рисунках, используется только один сенсор, регистрирующий компоненту x вектора x.

a xi (k)                    yji (k)

wji(z, k) j wj0(k)

Рис. 8. Примеры структуры синаптических весов НС в составе адаптивной системы, показанной на рис. 3, б.

а — основная модель фильтра; б — модель гамма-фильтра; в — модель фильтра Лагерра [27]

Применительно к этим структурам НС для ВФС Принсайп, Врие и Оливере (Principe, Vries, Olivere) [27] использовали фильтры Лагерра.

ПОСЛЕДОВАТЕЛЬНОЕ ИЗВЛЕЧЕНИЕ СИГНАЛОВ ИЗ СМЕСИ В ЗАДАЧЕ ВФС

При решении задачи разделения СИ и восстановления их формы в случае линейной смеси или смеси в виде свертки может быть использовано два подхода: в первом (кратко описанном выше) разделяются одновременно все СИ, во втором — выделяются сигналы последовательно, один за другим. Второй подход целесообразен, когда в многоканальной системе используется много сенсоров (электродов, микрофонов или других преобразователей), а информационно значимым является только малое число сигналов, поступающих на сенсоры (рис. 9).7

Неизвестная часть

Рис. 9. Структура системы, ориентированной на последовательное извлечение СИ или последовательный АГК.

Синаптические веса w_ij (свободные параметры НС) могут быть изменяемыми во времени коэффициентами или адаптивными фильтрами

Сигналы могут извлекаться в определенном порядке в соответствии с их статистическими признаками, например в порядке, определяемом величиной нормализованного эксцесса. (Логика такой процедуры тесно связана с логикой восстановления СИ из смеси в форме многоканальной свертки [28] и вместе с тем может трактоваться как обобщение анализа главных компонент (АГК), где де-коррелированные выходные сигналы извлекаются в порядке уменьшения значения их дисперсии). Последовательное извлечение СИ из смеси может выполняться с использованием последовательно связанных нейронных сетей, аналогично тому как это осуществляется при АГК.

Для таких систем целесообразна разработка алгоритмов обучения НС, устойчивых к небольшим уровням шума и позволяющих извлекать из смеси только небольшое число сигналов, которые представляют интерес и содержат полезную информацию.

ВОССТАНОВЛЕНИЕ ФОРМЫ СИГНАЛОВ

ИЗ СМЕСИ В ФОРМЕ МНОГОКАНАЛЬНОЙ СВЕРТКИ: МОДЕЛЬ ПРОСТРАНСТВА СОСТОЯНИЙ

Для общего случая наличия СИ и шума динамические системы смешивания сигналов и восстановления их формы могут описываться моделью пространства состояний (рис. 10), которая представлена соотношениями

5( k +1) = A • |( k) + B • s( k) + N • v_p (k), x( k) = C( k) • <( k) + D( k) • s( k) + v( k),

где ^ — вектор состояния системы; s(k) gRn — вектор неизвестных входных сигналов (предполагается, что компоненты его имеют нулевое среднее и негауссовы одинаковые и взаимно пространственно независимые распределения); x(k) — вектор сигналов сенсоров; ν_p (k) — вектор шума; (r x r)-матрица A — матрица состояния; (r x n)-матрица B — входная матрица смешивания; (m x r)-матрица C — выходная матрица смешивания; (m x n)-матрица D — матрица смешивания вход-выход; (r x p)-матрица N — матрица преобразования шума.

Передаточная функция является (m x n) -матрицей и имеет вид:

H(z) = C • (z • I - A)^-1• B + D,              (15)

где z¹ — символ операции задержки (т. е. z¹• x(k)=

= x(k -1)).

В аналогичной форме представляется модель системы, реализующей ВФС:

5( k +1) = A ^( k) + B • x( k) + L • vp (k), y( k) = C( k) • ^( k) + D( k) • x( k).

Соотношение (16) включает неизвестные матрицы пространства состояний: (M x M) -матрица A; (M x m)- матрица B; (m x M)- матрица C; (m x m)-матрица D и (M x m)- матрица L . При этом имеется в виду, что M > r, т. е. порядок системы ВФС

Динамический процесс смешивания

x(k)

а

Динамический процесс разделения

Рис. 10. Структура общей модели пространства состояний, включающей линейное смешивание (компоненты вектора состояния) (а) и адаптивную модель разделения (б) для динамического анализа независимых компонент.

Цель алгоритмов обучения состоит в оценке набора матриц {A, B, C, D, L}

должен быть не менее, чем порядок системы смешивания сигналов.

Концепция модели пространства состояния, отражающей общую форму смешивания сигналов источника и адаптивную процедуру их разделения при динамическом анализе независимых компонент, показана на рис. 10.

Можно считать, что линейная модель пространства состояния является расширением модели одновременного разделения сигналов и ВФС. В частном случае, когда матрицы A,B,C в модели смешивания и матрицы A,B,C в модели разделения сигналов являются нуль-матрицами, общая модель упрощается и отражает метод анализа независимых компонент. Элементы набора матриц Θ = [A, B, C, D, L] являются параметрами, которые определяются в процессе обучения на основе знания временнóй последовательности x(k) и, возможно, некоторых априорных знаний о системе в целом.

Таким образом, динамическое ВФС реализует получение вида первоначальных СИ по регистрируемым значениям x(k) без использования априорных знаний о СИ и о матрицах пространства состояний [A, B, C, D] . Передаточная функция, определяющая восстановление сигналов, имеет вид: W(z) = C • (z • I - A)^-1• B + D . Обычным (и практически неограничивающим) предположением

x(k)

Нелинейная часть

Линейная часть

Рис. 11. Упрощенная нелинейная модель разделения СИ.

При разомкнутом переключателе эта модель — класса скользящего среднего, при замкнутом переключателе — это рекуррентная (нелинейная) модель авторегрессии скользящего среднего (НАРСС) [29, 30]

является взаимная независимость СИ и равенство нулю их средних значений. В случае отсутствия шума СИ могут быть восстановлены по выходным сигналам y(k) = [y1(k),y2(k),...,ym(k)]T в соответствии с соотношением:

y( k) = [W( z) • H( z)] • s( k) = [D( z)] • P • s( k),     (17)

где P — обобщенная (m x n)-матрица перестановок (общего вида); D(z) — диагональная матрица с передаточными функциями D_ii (z) , определяющими форму фильтров⁸

D( z) = diag{D_n( z), D₂₂( z),..., Dmm (z)}.

В некоторых приложениях требуется, чтобы Dii (z) = Xiz-Ti, где Xi — постоянный ненулевой коэффициент масштаба, а τi — величина времен-нóй задержки.

НЕЛИНЕЙНАЯ МОДЕЛЬ ПРОСТРАНСТВА СОСТОЯНИЙ И ОБРАБОТКА ВЫХОДА МОДЕЛИ ДЛЯ ВФС

Линейная модель пространства состояний для смешивания сигналов и их разделения фильтрацией обобщается на нелинейную модель. Она представлена на рис. 11 и описывается соотношениями

К k) = f [ x( k ), ^ (k)], y (k) = C( k) • ^( k) + D( k) • x( k),

где ^(k) = [51(k),^2(k),...,^M(k)]T— вектор состояния; x( k) = [ %i( k), x2( k),..., xm (k )]T — доступный для измерения вектор сигналов сенсоров; f[x(k), ξ(k)] — M-мерный вектор нелинейных функций (с x(k) = [xT(k), xT(k -1),...,xT(k - Lx)] и I(k) = [^T(k), 5T(k -1),...,5T(k - Lx)] ); вектор сигналов на выходе системы y (k) = = [У1(k),y2(k),...,ym(k)]T; (mxM)-матрица C и (m x m)-матрица D — матрицы на выходе систе мы.

Первое соотношение в (18) описывает нелинейную модель авторегрессии скользящего среднего, а модель выхода системы, которая отражена вторым соотношением (18), является линейной. Цель состоит в оценке матриц выхода C и D

Нейронная сеть

ˆ

Рис. 12. Упрощенная модель нейронной сети с СФПН в применении для нелинейной структуры квази-ВФС для бинарных СИ на примере отдельного канала.

Переключатель в положении 1 — супервизорное обучение НС; в положении 2 — несупервизорное обучение

и в идентификации модели НАРСС с использованием нейронной сети, сигналов сенсоров x(k) и (желаемых) СИ s(k) (которые доступны для кратковременных временных окон).

Для того чтобы решить эту сложную задачу, используется подход квази-ВФС, т. е. комбинируются алгоритмы супервизорного ("с учителем") и несупервизорного обучения НС. Подход проверен в нескольких прикладных исследованиях.9 Обычно предполагается, что система смешивания СИ изменяется достаточно медленно, и ее параметры флюктуируют незначительно (главным образом за счет изменения локализации СИ в пространстве). Обучающие СИ (ОСИ) доступны только в течение кратковременных интервалов. В течение интервалов, когда ОСИ недоступны, может использоваться алгоритм несупервизорного обучения, который выполняет тонкую подстройку выходных матриц C и D (при сохранении фиксированной нелинейной модели). Таким путем можно непрерывно оценивать СИ. Упрощенная структура нелинейной модели пространства состояния, использующей НС с СФПН [31, 32], показана на рис. 12.

Тот факт, что модель пространства состояний является полезным и эффективным средством при решении прикладных задач ВФС по измерениям их смеси, обусловлен рядом обстоятельств.

• -    Процессы смешивания сигналов и разделения фильтрацией неизвестных СИ sj(k) (j = 1, 2,…, n) могут иметь различную математическую или физическую модель, зависящую от специфики приложения. Модель пространства состояний для разделения сигналов является гибкой и универсальной моделью, которая описывает широкий класс динамических систем, включая систему многоканального смешивания сигналов в форме свертки в условиях конечной импульсной характеристики

фильтров, гамма-фильтров или более общих моделей (авторегрессии, скользящего среднего или авторегрессии скользящего среднего)

– Такие модели динамического разделения сигналов позволяют создавать многие прототипы соотношений той же самой динамической системы посредством применения эквивалентных преобразований.

• -    Линейная модель пространства состояний является расширением модели одновременного разделения СИ с восстановлением их вида.

• -    Модель пространства состояний включает две подсистемы: слой линейного выхода (без запоминания) и линейную или нелинейную рекуррентную НС, которую можно идентифицировать или подстраивать с использованием различных методов обучения и подстройки параметров нейронной сети [33, 34].

ОБЛАСТЬ ПРИЛОЖЕНИЙ ОБРАБОТКИ СИГНАЛОВ С РАЗДЕЛЕНИЕМ (КВАЗИРАЗДЕЛЕНИЕМ) СМЕСИ

Задачи анализа независимых компонент (АНК), восстановления вида первичных сигналов источника (СИ) при линейной их смеси и смеси в форме многоканальной свертки потенциально могут иметь применение в различных приложениях и областях исследований. Это — обработка и анализ биомедицинских сигналов: электроэнцефалограмм (ЭЭГ), магнитоэнцефалограмм (МЭГ), электрокардиограмм (ЭКГ); обработка геофизических данных; многоаспектный, интеллектуальный анализ баз данных сложной структура ("data mining"); усиление речевых сигналов (ВФС при наличии шума); распознавание изображений и совершенствование системы беспроводной связи [1, 8, 35–38]. В этих приложениях бывает доступным большое количество сигналов сенсоров или данных, которые являются фильтрованной суперпозицией отдельных различных и независимых СИ, а цель состоит в обработке наблюдений таким образом, чтобы выход соответствовал разделенным первичным СИ.

Обработка и анализ биомедицинских сигналов осуществляется в связи со следующими исследованиями.

• -    Восстановление сигнала ЭКГ плода (т. е. удаление или фильтрация сигнала ЭКГ матери от ЭКГ плода). Отделение сигнала ЭКГ трансплантированного сердца от сигнала ЭКГ "старого" сердца [39].

• -    Разделение сигналов ЭЭГ средствами анализа независимых компонент.

• -    Удаление артефактов и шумов из регистрируемых ЭЭГ и МЭГ. Усиление компонент ЭЭГ и МЭГ с низким уровнем.

Акустические приложения включают ситуации, в которых СИ — это сигналы от различных микрофонов в звуковом поле, производимом несколькими людьми (задача выделения индивидуального речевого сигнала), или СИ — это сигналы от нескольких акустических преобразователей в подводном звуковом поле от шума двигателей нескольких судов (задача гидроакустического контроля).

Примеры радио- и беспроводной связи включают наблюдения, соответствующие элементам массива с выхода антенны (как отклик от нескольких передатчиков), и могут также включать эффект взаимной связи элементов. Другая возможная ситуация в области радиосвязи включает использование поляризационного мультиплексирования в звеньях микроволнового оборудования; поддержание ортогональности поляризации не может быть совершенным и остается небольшая интерференция между отдельными передающими каналами. В радиолокационной технике встречается наложение сигналов за счет различных механизмов модуляции сигналов от целей, наблюдаемых несколькими приемниками с различной чувствительностью и компонентам поляризации.

ЗАКЛЮЧЕНИЕ

Рассмотрены возможные подходы и методы, позволяющие получать форму отдельных сигналов по измерительной информации об их смеси. Основой алгоритмов и нейросетевых структур, реализующих восстановление сигналов — компонент смеси, служат различные концепции, связанные с особенностями формирования смеси сигналов, наличием статистических характеристик шума, сопровождающего регистрируемые сигналы на сенсорах, а также с методологией снижения уровня шума в восстановленных сигналах.

– Приведены элементы общей концепции смешивания первичных сигналов источника (СИ), их фильтрации и разделения при наличии шума или без него.

– Проанализированы типы формализации задачи восстановления формы сигналов (ВФС) и варианты постановки задач, которые связаны с выделением части сигналов из смеси (по критерию максимальной доли в общей дисперсии или по критерию наибольшей независимости выделяемых сигналов).

– Даны структуры преобразований, обеспечивающих реализацию полного восстановления первичных сигналов источника (СИ) или последовательное выделение компонент вектора сигнала, который регистрируется сенсорами в форме смеси неизвестного вида.

– Кратко описана методология использования нейронной сети и адаптивного алгоритма обучения, позволяющие получить оценку СИ, смешивающей матрицы H и разделяющей матрицы W.

– Даны трактовка задачи ВФС как задачи анализа независимых компонент и метод использования критерия Кульбака—Лейблера для оценки степени независимости компонент.

– Концепция и типы формализации задачи ВФС приспособлены к особенностям приложений и построены с использованием нескольких модификаций анализа независимых компонент (АНК).

– Проанализированы особенности задачи разделения СИ для многоканальной смеси в форме свертки и показана логика процедур для решения такой задачи.

– Рассмотрена модификация задачи ВФС, решение которой основано на последовательном извлечении сигналов из смеси. Сигналы могут извлекаться в определенном порядке в соответствии с их статистическими признаками.

– Дан метод решения задачи ВФС из смеси в форме свертки на основе модели пространства состояний. Модель отражает форму смешивания СИ и адаптивную процедуру их разделения при динамическом анализе независимых компонент.

– Показана область приложений обработки сигналов с целью восстановления вида компонент регистрируемой смеси.