Выделение слабого сигнала из некогерентного шума

Проблема выделения полезного сигнала при отношениях сигнал/помеха, значительно меньших единицы, и при минимальных априорных предположениях относительно формы полезного сигнала и характеристик шума по-прежнему привлекает внимание исследователей.

В настоящей работе обсуждается задача построения фильтра, основанного на различии фазовых свойств измеряемого сигнала и искажающей его помехи. Фаза измеряемого сигнала считается регулярной, а фаза шума – случайная функция, кроме того, предполагается, что математическое ожидание шума равно нулю.

В работах [1, 2] показано, что подобный фильтр может быть построен с использованием опорного импульса специального вида (рис. 1).

Импульс имеет две прямоугольные ступени с амплитудами U 1 и U 2 соответственно, общая длительность ступеней незначительно меньше длительности интервала наблюдения T н . Обозначим T и длительность опорного импульса, при этом M = Т _н /Т и , D = U 2 /U 1 . При проведении измерений фрагмент измеряемого сигнала S помещается на вторую ступень опорного импульса, а в качестве измеряемой характеристики вычисляется фаза основной гармоники e j^' при ш = 1 Для оценки величины сигнала используется разность фаз опорного импульса с сигналом и без него.

Как показали результаты анализа, при значениях D и M , близких к единице, увеличивается чувствительность фазы к изменению напряжения (амплитуды ступени). При этом зависимость фазы от D и M имеет вид

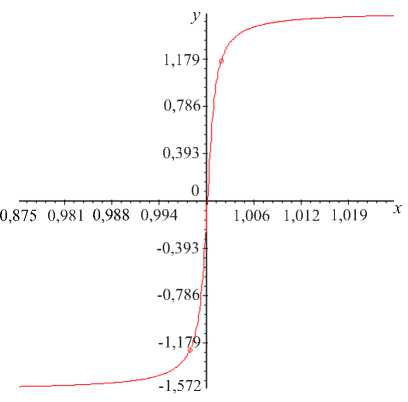
Рис. 2. Зависимость значения фазы основной гармоники опорного сигнала от отношения амплитуд первой и второй ступеней

1 - D ^п v < - ) = "•* 1+ d ^tg 2mm

На рис. 2 показана зависимость фазы гармоники спектра импульсного сигнала с частотой ω от D . Видно, что при переходе этого отношения через единицу значение фазы изменяется скачкообразно практически от - π /2 до π /2.

Подбирая параметры D и M , можно обеспечить соответствие размеров опорного импульса и измеряемого сигнала, так чтобы значения фазы импульса с сигналом и без него попадали на концы квазилинейного участка графика, как показано на рис. 2 (точки на кривой).

Важным параметром, определяющим эффективность описываемого фильтра, является глубина модуляции. Анализ показывает, что максимальная глубина фазовой модуляции может быть равна π (гармоники находятся в противофазе). Однако в реальных расчетах рекомендуется обеспечивать попадание фазы опорного импульса и фазы импульса с измеряемым фрагментом сигнала на квазилинейный участок графика зависимости фазы от параметра ф ( D ). Для этого первую ступень опорного импульса принимаем равной единице, а затем вычисляем значение D , обеспечивающее попадание начальной фазы основной гармоники ( ш =1) на нижний конец квазилинейного участка кривой ф ( D ), который соответствует значениям D , приближенно равным 0,1 от максимума второй производной ф ( D ) по D . Этот максимум равен ф ( D ) _max = ( — sin а ) / (cos 2 а ).

Сформировав таким образом опорный импульс, вычислим среднее значение измеряемого фрагмента сигнала и умножим этот фрагмент на коэффициент а = 2(1 — D ) /х, где X — среднее значение фрагмента “сигнал плюс шум”. Такой выбор размеров опорного импульса и измеряемого фрагмента сигнала обеспечивает значение разности начальных фаз основной гармоники порядка 2,5 ^ 2,9 рад.

Проведены модельные расчеты для нескольких типовых сигналов.

Исходный опорный импульс имел следующие параметры: количество точек отсчета — 64, количество точек отсчета с нулевой амплитудой — 1, высота первой ступени — 1, D = 0,8516. В качестве модельного сигнала использовался полином второго порядка с коэффициентами, равными 1, 1, -1. К этому сигналу добавлялся случайный нормально распределенный шум

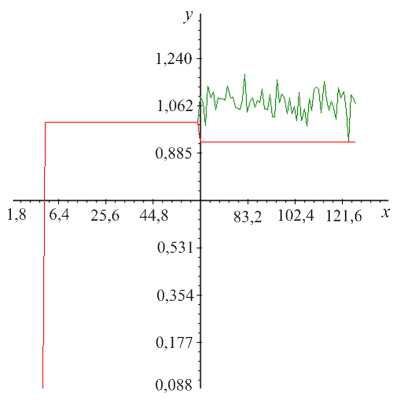
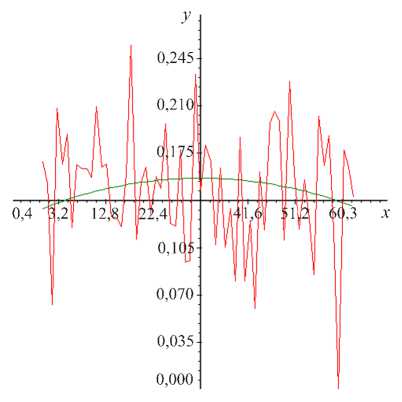
Рис. 3. Опорный импульс с добавленным фрагментом Рис. 4. Сигнал (зеленый) и сигнал сигнала с шумом (в четвертом квадранте —         с добавленным шумом (красный)

исходная вторая ступень опорного импульса)

с нулевым математическим ожиданием и дисперсией, равной 0,2. Полученный в результате импульс представлен на рис. 3, 4.

Вычисленная начальная фаза основной гармоники опорного импульса равна -1,22956, а начальная фаза той же гармоники для опорного импульса с фрагментом сигнала без шума равна 1,31312. Таким образом, разность фаз составила -2,54268 рад.

Поскольку все гармоники, на которые разлагается сигнал с помехой в интервале T и /2, за исключением гармоники ω =0, кратны основной гармонике, они не дают вклада в изменение фазы этой гармоники. Следовательно, изменение фазы этой гармоники при добавлении измеряемого сигнала обусловлено только вкладом нулевой гармоники сигнала с шумом. Таким образом, среднее значение измеряемого сигнала может быть оценено через разность фаз основной гармоники опорного импульса с сигналом и без сигнала в виде

S =     ² a [tg⁽ ФВ1 ) ~ tg⁽ Vsi ^)]

[ a + tg( Фв1)][ a + tg( фsI)] A’ где tg(п/(2M)) = a; tg(фВ1) — тангенс фазы опорного сигнала.

Проведены расчеты по восстановлению сложного сигнала путем оценки средних значений отдельных его фрагментов. Для этого был сформирован исходный сигнал в виде импульса с колоколовидной огибающей вида

s ( t ) = Ae ^в t cos(2 nf ₀ 1 + ф о )

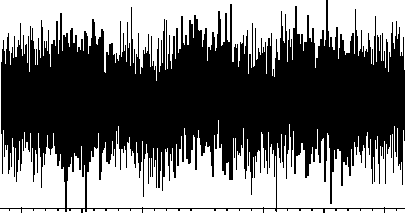
с параметрами A = 0 , 2; в = 0 , 5; ф о = 0; f о = 0 , 4. К этому сигналу добавлен шум в виде последовательности случайных нормально распределенных чисел. Соотношение сигнал/шум составляло порядка 0,2. Зашумленный сигнал разбивался на фрагменты по 32 точки, для каждого такого фрагмента описанным выше способом оценивалось среднее значение сигнала. Полученный результат представлен на рис. 5.

А

а

1,047

-1,069

94 397 1587 2778       5158 6349 7539

N

А

б

1,047

-1,069

94 397 1587 2778       5158 6349 7539 N

А

в

1,047

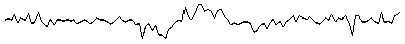
-1,069

94 397 1587 2778

5158 6349 7539 N

А

г

1,047

-1,069

94 397 1587 2778

5158 6349 7539 N

Рис. 5. Результаты выделения зашумленного сигнала:

а — исходный зашумленный сигнал; б — исходный сигнал без шума; в — сигнал, восстановленный с помощью фильтра; г — восстановленный сигнал, сглаженный с помощью скользящего среднего

Результаты проведенного исследования показывают, что предложенный метод достаточно эффективен при восстановлении сильнозашумленного сигнала при минимальных априорных предположениях о характере помехи.