Выявление артефактов сердца методами преобразований спектров с применением окна поиска

Распознаваниеартефактовнаповерхностисер-дечно-сосудистого пучка рентгеновских снимков в целях установления диагностики заболеваний имеет актуальное значение в медицине. Это свя- зано с тем, что современная визуализация в рентгенографии региональных учреждений ни ограничивается просмотром снимков на молочно-белых экранах. В этих случаях разрешающая способность органа зрения небольшая в чернобелых снимках. Применяя цифровую обработку снимков с помощью сканеров, можно несколько увеличить разрешение. Но и это не позволяет выявлять отдельные артефакты на изображениях.

Большинство отделов сердечно-сосудистой системы, являясь мягкоткаными образованиями, находятся в неблагоприятных условиях для осуществления общих методов рентгенологического исследования. Не имея значительных отличий в плотности, химическом составе и объеме, тени этих образований сливаются с тенями окружающих органов и тканей. Исключения составляют большая часть периметра сердца, примыкающие к нему крупные сосуды. Обследование этой части сердечно-сосудистой системы сравнительно более доступно, поскольку она проецируется на фоне воздушных легких.

В работе предлагается, используя дигиталь-ную обработку, применить современные математические методы преобразований, например, Фурье-образ двухмерного дискретного сигнала и ряд других преобразований, описанных ниже, увеличить изображение с целью выявления артефактов на поверхности сердечно-сосудистого пучка рентгеновского отображения.

Решение проблемы

Для преобразования непрерывных сигналов в цифровую форму прибегают к дискретизации сигналов с помощью сканеров и дальнейшей операционной обработки программными средствами, например, программой АСDSee v.10, затем полученное отображение подвергнуть дискретизации.

Самый распространенный способ дискретизации сигналов основывается на теореме отсчетов. Сигналы, спектр Фурье которых равен нулю за пределами интервала ( ^-® 0 , ® 0 ) могут быть путем интерполяции восстановлены по своим отсчетам, взятым с шагом T < 1/(2ю₀) .

Обозначим f ( t ) дискретное представление непрерывного сигнала f ( t ), тогда Фурье-образ дискретного сигнала F n ( го ) :

∞ f ,(t) = f (t) S 6(t - nT),        (1)

n =-∞

∞

F , (®) = J f , ( t ) e^" ⁾ dt ,       (2)

-∞ соответствует свертке Фурье-образа непрерывного сигнала F(го) с Фурье-образом гребенки Дирака:

∞

Fn ( to ) = f ( to ) 8 1 S 5 I to - П\ =

T ⁿ =-” ^ T ^              (3)

= 1 f F | to - n I = 2 to_n f F (to - 2 to_n n ,

00 n =-∞ ⎝      ⎠        n =-∞

⊗ - символ свертки. Таким образом, спектр дискретного сигнала представляет собой периодическое повторение (с периодом 2ω₀ ) спектра непрерывного сигнала.

Из рис. 1а видно, что в первом по дискретному спектру можно точно определить непрерывный спектр, а, следовательно, и восстановить непрерывный сигнал. Поскольку спектр преобразованного сигнала имеет ограниченное значение, диктующее теоремой Котельникова и в этом случае теряется часть информации в высокочастотной части изображения, то спектр преобразования необходимо с периодом T >  l/(2^₀). Однако в этом случае спектр получается перекрывающийся, как показано на рис. 1б, то есть спектр будет перекрывающийся. Это невозможно из-за наложения «хвостов» – высокочастотные составляющие спектра непрерывного сигнала попадают в область более низких частот в спектре дискретного сигнала, и часть информации, содержащейся в непрерывном сигнале, необратимо теряется при дискретизации.

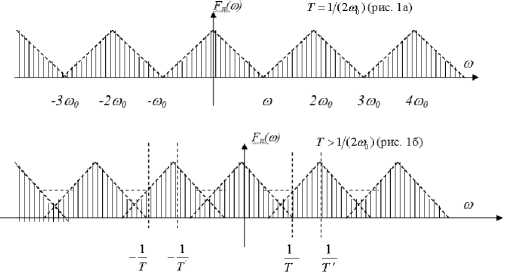
Рис. 1. Эффект наложения спектров при дискретизации с шагом большим, чем определяет теорема Котельникова

С учетом (3) спектр непрерывного сигнала

F(o)                               Fn (®)

можно определить следующим образом:

F (ro) = F n (to) • H (rn) := F n ( to) • rect

ω + ω ₀

^2to 0

rect ( x ) =

fl,

I ^0,

x = 0

иначе

Тогда непрерывный сигнал находится через обратное преобразование Фурье:

∞

f(t) =— JF (to) • rect 2n

-∞

ω + ω ₀

2tofi

• e^d to , (5)

Что соответствует свертке Фурье-образов:

f (t) = fn (t) ® h(t) := fn (t) ® 2tooSinc(2ntoot) = co

= 2to0 j/;(r)sinc[2^o(?_r)]^r ,

-co

sin(n x)где sinc(x) = —-—-.

πx

Учитывая (1) выражение (6) можно переписать в следующем виде:

∞

f(t) = Z f(nT)sinc[2ntoo(t - nT)]. (7)

n=-∞

Для последовательностей конечной длины соотношение (7) можно аппроксимировать с помощью пары прямого и обратного сдвинутого дискретного преобразования Фурье (ДПФ). Интерполяцию дискретного сигнала можно производить также с помощью стандартного ДПФ, симметрично дополняя спектр сигнала нулями до длины, во столько раз превышающей длину исходного спектра, сколько требуется дополнительных отсчетов на один отсчет исходного сигнала.

Производя замену непрерывных переменных на дискретные отсчеты, зная, что д N отсчетов: t = nT , to = m 2 to 0 /N получим:

N 2          nm

∑ i 2 π

FmeN , m=-NJ 2

n и для промежуточных отсчетов t = — T :

k

kN /2           .. nm

__ i 2 n

F ,e    kN •

m , k^         • m = -kN 12

jF m , m e [ -N/ 2, N/2 ]

F= m,k ⎪⎩0, иначе kN - новая размерность спектра. При kN = 2 p+l пропорциональном степени двойки данный алгоритм легко реализуется с помощью быстрого преобразования Фурье (БПФ).

Экстраполяция спектра используется для повышения разрешающей способности при формировании изображений различными системами, используя дополнительную априорную информацию о сигнале можно решить задачу аналитического про- должения спектра за полосу пропускания системы формирования.

Если функция ограничена на некотором интервале, кусочно-непрерывна и интегрируема на этом интервале, то ее спектр является аналитической функцией. Следовательно,при знании спектра сигнала в некоторой области его можно экстраполировать на всю комплексную область,в частности, разложением в некоторый функциональный ряд. В [1]приведена процедура разложения по системе сфероидальных волновых функций,обладающих двойной ортогональностью: на симметричном ограниченном и неограниченном интервале. Однако метод аналитического продолжения в чистом виде чрезвычайно чувствителен к шумам, что приводит к необходимости принимать специальные меры по ограничению числа членов ряда, введению весовых коэффициентов.

Если применять итерационный алгоритм Герш-берга-Папулиса,то используется та же априорная информация – принадлежность к классу финитных функций и знание низкочастотной составляющей спектра. Способы управления сходимостью итерационного алгоритма и регуляризации в присутствии шумов подробно рассмотрены в [5].В этом случае дополнение спектра нулями по формуле (9)можно рассматривать как первую итерацию.

При этом нужно отметить,что экстраполяция спектра нулями,обеспечивая высокую скорость обработки изображений,в то же время вносит нежелательный эффект Гиббса,который особенно заметен придетальномрассмотрениибольшихучастковизоб-ражения с равномерной яркостью.Частично компенсировать данный эффект можно весовой обработкой спектра изображения.Конкретный вид весовой функции можно задавать из разных соображений.

Так,например,из теории статистической оптики известно, что когерентная оптическая система линейна по амплитуде,в то время как некогерентная систе-малинейнапоинтенсивности.Тоесть,частотно-пере-даточная функция (ЧПФ)некогерентной оптической системы равна Фурье-преобразованию от функции интенсивности импульсного отклика и,следователь-но,свертке функций зрачка.Функцией зрачка в нашем случае выступает прямоугольная функция:

H (ω

Λ(

'i-|4 |x|

to + to0 2to0

здесь H( to ) - ЧПФ некогерентной системы.

Вид частотно–передаточной функции для некогерентной и когерентной систем приведен на рис. 2. Видно, что она охватывает в два раза более широкий диапазон частот, чем функция прямоугольного окна, одновременно подавляя высокие частоты.

Подавление высоких частот применяется для устранения строб-эффекта, состоящего в неточном восстановлении сигнала из-за наложения «хвостов» спектра. В этом случае часто используют в качестве частотно-передаточной функции (ЧПФ) функцию Гаусса [1]:

обеспечении Alchemy - билинейная (рис. 4б) и квадратичная (рис. 4в).

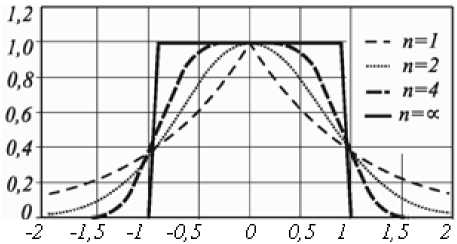
Рис. 3. Вид весовой функции (1 1) для различных значений параметра и при т с= т о = 1

H ( to ) = exp

-

ω _c – параметр, определяющий эффективный размер весовой функции или функции зрачка H(to ) >  0.

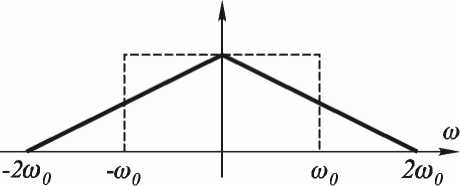
Рис. 2. Частотно-передаточная функция для когерентной (штриховая линия) и некогерентной (сплошная линия) систем

Прямоугольная интерполяция, обладая наилучшими скоростными характеристиками, является самой грубой.

Билинейная интерполяция, улучшая качество, требует больших затрат времени. Для сплайн-ин-терполяции нужно еще больше времени. Во всех случаях параметры «качество» и «скорость» носят конкурирующий характер.

Однако в работе предлагается использовать весовую функцию типа «гауссовой» вида:

⎪ exp H( ω ) =⎨

⎝

ω

ωn ⎟ c⎠

,

0 ≤ ω≤ω0

. (12)

0, иначе

Рис. 4. Фрагменты изображения различными методами: прямоугольная интерполяция (рис. 4а) «сверхразрешение», полученное экстраполяцией: n = ω _о -прямоугольное окно, когерентный случай (рис. 4б), n = 8, ω _с = 0.9 ω _о - «гауссово» окно (рис. 4в)

Такая функция позволяет охватить широкий диапазон ЧПФ. Действительно, при n = 1 она близка к «треугольной» функции (10) некогерентной оптической системы, при n = 2 это функция Гаусса (11), с ростом параметра n она приближается к прямоугольной функции (4) и совпадает с ∞. Второй         ωс позволяет ре гулировать степень подавления высоких частот. На рис. 3 приведен вид функции (11) для различных значений параметра и при тс= то = 1.

Рис. 4 служит иллюстрацией различных методов интерполяции изображений, упомянутых выше: прямоугольная интерполяция (рис. 4а), интерполяция, реализованная в программном

Видно также и преимущество метода экстраполяции спектра, состоящее в том, что мелкие детали изображенияувеличиваютсябезразмытия,счетким сохранением формы.В этом существенное отличие от масштабирования методом билинейной интерполяции. Чтобы достичь таких результатов,нужно проводить интерполяцию сплайнами не ниже третьего порядка, что требует много времени.

Лучший результат достигается при использовании «гауссового» окна (рис. 4в). В дальнейшем окончательная обработка производится фильтрацией, с использованием медианного фильтра, который широко распространен в обработке изображений.