Выявление хаотических процессов в динамической системе фондового рынка по фьючерсным котировкам природного газа

Неэффективность применения традиционной линейной парадигмы анализа состояния фондовых рынков в условиях нестабильности детерминирует проведение исследований рынка ценных бумаг как динамической системы на выявление нелинейности и наличия в ней хаотических процессов. Исходными данными для анализа является временной ряд, представляющий собой ежедневные максимальные значения котировок фьючерсных контрактов на Нью-Йоркской бирже за период с 1 января 1998 г. по 31 декабря 2017 г. В целях увеличения стационарности ряда и снижения количества излишней входной информации, при анализе используются относительные изменения значений за каждый из промежутков времени (рис. 1).

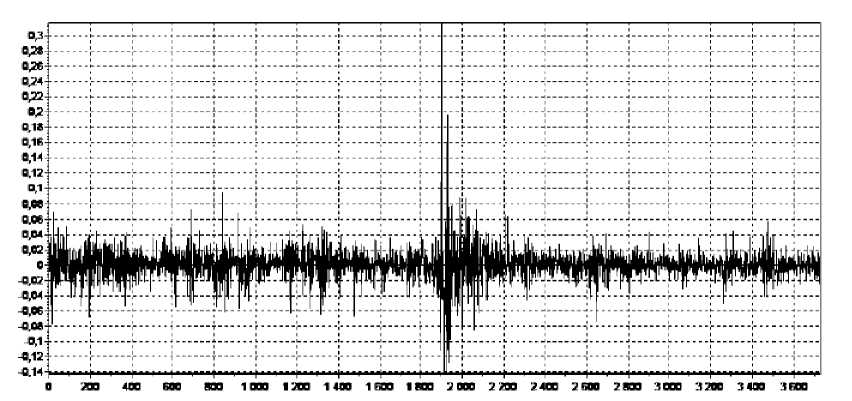
Рисунок 1 – Исходные данные для анализа: временной ряд нормированных приращений значений фьючерсных котировок на природный газ, 1.01.1998 – 31.12.2017 гг.

C целью нахождения временной задержки сигнала и размерности вложения исследуемых временных рядов были использованы два программных продукта: FRACTAN и DataPlore.

Для выбора временной задержки сигнала применяются различные методы, один из которых – метод автокорреляционной функции, основанный на предположении, что подходящей временной задержкой является минимальная, при которой координаты реконструированного аттрактора максимально независимые. Для исследуемого временного ряда первое приближение графика автокорреляционной функции к нулю в точке 1 (рис. 2), следовательно, наиболее подходящая временная задержка в соответствии с данным методом равна 1.

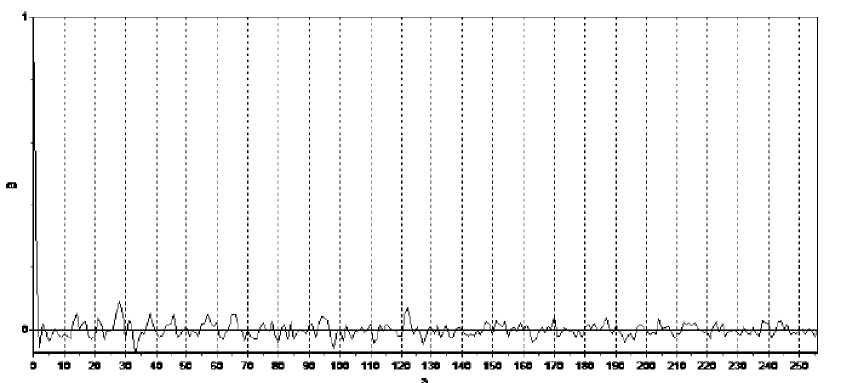
Рисунок 2 – График автокорреляционной функции для временного ряда нормированных приращений значений фьючерсных котировок на природный газ

Таким образом, для исследуемого временного ряда вычисление наиболее подходящей временной задержки определяет временную задержку τ равной 1 (1 день).

Далее необходимо выбрать размерность m пространства вложения, оценка которой может быть проведена различными методами, среди которых метод ложных ближайших соседей. Посредством метода ложных ближайших соседей возможно определить минимальное значение размерности пространства вложения m, такое, что при переходе к размерности (m+1) количество ложных соседей (точек аттрактора, близких друг к другу в Rm и отстоящих далеко в Rm+1) будет относительно мало. Вычисленное данным методом значение определяет наименьшую размерность пространства вложения, для которого возможна реконструкция аттрактора без самопересечений.

На рисунке 3 представлен график для определения размерности пространства вложения в соответствии с методом ложных ближайших соседей для исследуемого финансового временного ряда, так, для временного ряда нормированных приращений значений фьючерсных котировок на природный газ значение размерности пространства вложения равно 5.

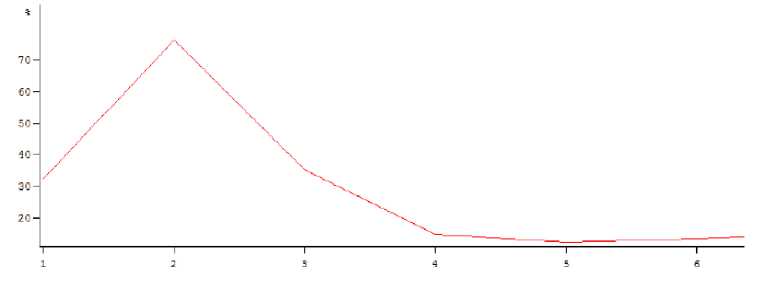
Рисунок 3 – График FNN для временного ряда нормированных приращений значений фьючерсных котировок на природный газ

Таким образом, выше были рассмотрены и апробированы на модифицированных временных рядах значений фьючерсных котировок на природный газ методы, позволяющие определить параметры вложения динамических систем по временному ряду, генерируемому системой. В ходе анализа нелинейных свойств исследуемых временных рядов было установлено, что первично требуемый показатель – временная задержка – равен для анализируемых данных – 1 день. Наиболее подходящей оценкой размерности пространства вложения будет определенная методом ложных ближайших соседей и равная 5 для временного ряда нормированных приращений значений фьючерсных котировок на природный газ.

Расчет старшего показателя Ляпунова для исследуемого временного ряда был выполнен с использованием программного продукта DataPlore. Старший показатель Ляпунова для модифицированных временных рядов значений фьючерсных котировок на природный газ составляет 1,49, что говорит о подтверждении выдвинутой в данной работе гипотезы о наличии хаотических свойств анализируемых финансовых временных рядов.