Выявление однородных партий изделий космической радиоэлектроники на основе разделения смеси сферических гауссовых распределений

Введение. EM-алгоритм (максимизация математического ожидания) успешно применяется для статистических задач, связанных с анализом неполных данных, когда некоторые статистические данные отсутствуют, либо для случаев, когда функция правдоподобия имеет вид, не допускающий удобных методов исследования, но допускающий серьезные упрощения при введении дополнительных «ненаблюдаемых» («скрытых») величин [1]. Именно такая постановка задачи (кластеризация многомерных данных нормального распределения со скрытыми данными) используется нами для решения задач разделения ЭРИ по производственным партиям исходного сырья.

Пусть плотность распределения на множестве X имеет вид смеси k распределений (предполагаем, что распределения гауссовы):

kk

ρ ( x ) = ∑ α _j ρ _j ( x ), ∑ α _j = 1, α _j ≥ 0, j =1 j =1

где ρ j ( х ) – функция правдоподобия j -й компоненты смеси; α j – ее априорная вероятность, а функции правдоподобия принадлежат параметрическому семейству распределений φ( x ;θ) и отличаются только значениями параметра ρ j ( х ) = φ( x ;θ). Задача разделения смеси (нечеткой кластеризации) заключается в том, чтобы, имея выборку X ^N случайных и независимых наблюдений из смеси ρ( х ), зная число k и функцию φ, оценить вектор параметров распределения Θ = (α 1 , …, α k , θ 1 , … θ k ).

Искусственно вводится вспомогательный вектор скрытых переменных G , который может быть вычислен, если известны значения вектора параметров Θ.

EM-алгоритм состоит из итерационного повторения двух шагов. На E-шаге вычисляется ожидаемое значение вектора скрытых переменных G по текущему приближению вектора параметров Θ. Обозначим через ρ( х , θ j ) = ρ( х ) Ρ (θ j | x ) = α j ρ j ( x ) плотность вероятности того, что объект x получен из j -й компоненты смеси. Обозначим

k gij ≡P(θj |xi)=αjρj(xi)/∑αsρs(xi)

s =1

апостериорную вероятность того, что обучающий объект x_i получен из j- й компоненты смеси.

На M-шаге решается задача максимизации логарифма правдоподобия

N Nk

Q ( Θ ) = ln ∏ _{i = 1} ρ ( x _i ) = ∑ ln ∑ α _j ρ _j ( x _i ) → max _Θ i =1 j =1

и находится следующее приближение вектора Θ по текущим значениям векторов G и Θ. M-шаг сводится к вычислению весов компонент α j и оцениванию параметров θ j путем решения k независимых оптимизационных задач.

Данный алгоритм не позволяет определять количество k компонентов смеси (количество кластеров), поэтому должна решаться серия задач с различным предполагаемым числом кластеров. Кроме того, EM-алгоритм обладает сильной неустойчивостью по начальным данным [1]. Тем не менее, к его преимуществам можно отнести [2] то, что его можно комбинировать с другими алгоритмами обработки данных, также для его использования не требуется выделения метрик. При применении более распространенной модели k- средних к задаче выделения однородных производственных партий электрорадиоизделий (ЭРИ) проблема выбора метрики или меры расстояния [3] не имеет однозначного решения. На практике приходится использовать сложные специальные способы нормировки данных [4].

EM-алгоритм успешно работает с малыми объемами данных. Некоторые дорогие виды электрорадиоизделий, несущие в космических аппаратах наибольшую функциональную нагрузку, поступают партиями от нескольких штук, что делает применение EM-алгоритма и алгоритмов на его основе весьма перспективным применительно к нашей задаче.

Простые эксперименты с реализацией EM-алгоритма в среде моделирования R для автоматической группировки партий ЭРИ от 50 до 620 штук (рис.1, 2) показывают [5], что данный алгоритм способен эффективно разделять смесь распределений, получая адекватные результаты, соответствующие реальным производственным партиям ЭРИ, если для выборки можно выделить несколько (не более 10) информативных признаков.

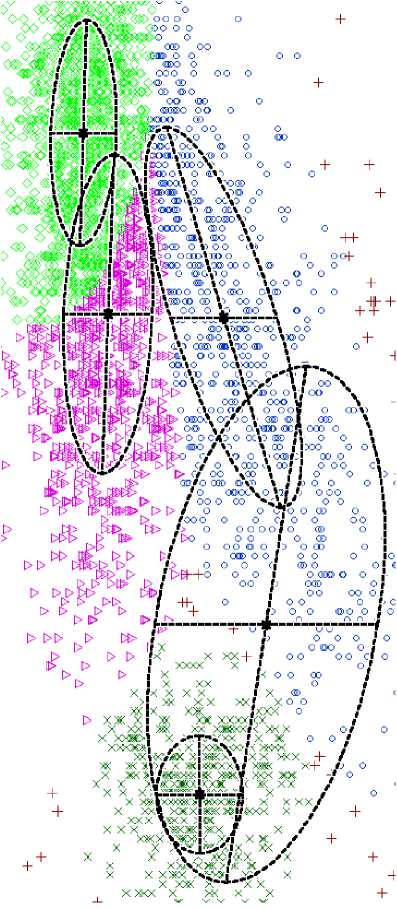
Кроме определения принадлежности каждого ЭРИ (точки на диаграмме) к кластеру, алгоритм дает таблицу с вероятностными характеристиками принадлежности к кластеру и показывает форму кластера, визуализируя возможные корреляции параметров ЭРИ. В то же время, работа алгоритма при использовании многомерных данных, какими являются данные неразрушающих испытаний ЭРИ, приводит к «зависанию» алгоритма, требует значительных вычислительных ресурсов, особенно в случаях, если число измерений приближается к числу группируемых объектов (векторов данных). Выделение информативных признаков – сложная задача. Так, на рис. 2 видно, что по двум признакам очень трудно выделить партии изделий. В то же время, обработка всех 205 признаков позволяет сделать это с весьма высокой точностью.

Создание модификаций EM-алгоритма с повышенной устойчивостью результата откроет новые перспективы в решении задачи автоматической группировки ЭРИ по производственным партиям, в частности, при небольшом объеме входных данных. Данной проблематике и посвящена настоящая статья.

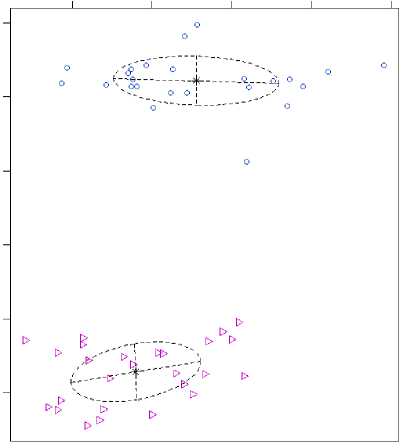
Рис. 1. Срез (показаны 2 параметра из 32) результата автоматической группировки усилителей 140УД25АС1ВК

Рис. 2. Разбиение сборной партии ЭРИ 1526ИЕ5 на 3 и 5 групп

Свойства сферических гауссовых распределений.

Сферическое гауссово распределение [6] N (ц, a ² I n ) определено на x е R n с плотностью

Р ⁽ x ) =

(2 п ) n /² a ⁿ

exp

II x -^11

2a2

где ||-|| - евклидово расстояние. Если X = (X1, ..., Xn) случайно выбраны на распределении N(0, a2In), тогда их координатами будут независимые случайные переменные с одинаковыми распределениями N(0, a2). Каждая координата имеет ожидаемое значение дисперсии a2 такое, что ц(| XI |2 ) = ц( X2 +... + X2 ) = na2.

Из теории больших отклонений [7], связанной с тем, что || X || ² будет плотно сконцентрировано вокруг n a ², следует

P (|l X 112 — n a ² 1 >^s n a ² )< e n ^E /24

Таким образом, большая часть плотности вероятности N (0, a ² I n ) укладывается в тонкую оболочку с радиусом a 4n от основания [6]. Это не противоречит факту того, что плотность гауссова распределения будет максимальной у центра, когда площадь поверхности на расстоянии r от основания - 0 <  r < a 4n , увеличивается быстрее, чем уменьшается плотность с расстоянием r [8].

Рассмотрим гауссово распределение N (0, a ² I n ), имеющее радиус aV n . Распределения N (Ц 1 , a 1 ² I n ) и N (ц₂, a ₂ ² I n ) на R n будем называть с- разде-ленными [9], если выполняется условие II ц 1 — ц ₂1 I >  c max { a 1 , a ₂ } 4n .

Смесь гауссовых распределений является с- разде-лённой, если все распределения в ней попарно с -разделены. Будем считать, что c ij определяет разделение между i- м и j- м распределением и c = min i ^ c ij . Мы можем обоснованно ожидать, что сложность исследования смеси гауссовых распределений повыша-

ется с понижением значения c .

При c = 2 (т. е. при 2-разделенной смеси) кластеры в основном не пересекаются. При больших размерно-

стях пространства n это утверждение верно даже для 1

₁₀₀ -разделенной смеси. Если c мало, то проекция

смеси на любую одну координату будет выглядеть унимодальной (частотная гистограмма имеет единственный пик). Это также может быть верно для проекции на несколько координат. Но для больших n , при совместном рассмотрении всех координат, распределение прекратит выглядеть унимодальным (слово «выглядит» обретает буквальный смысл, например, при использовании MDS-визуализации [10]). Именно это обстоятельство часто обусловливает использование данных большой размерности: там, где объекты практически невозможно разделить по одному или нескольким признакам, использование большой совокупности признаков позволяет добиться результата.

Например, в [6] авторы продемонстрировали данное свойство многомерных сферических распределений на 256-мерном наборе дискретных данных, состоящем из рукописных символов, собранных почтовой службой США.

Известные подходы к выделению однородных партий изделий. В настоящей статье задача разделения производственных партий электрорадиоизделий (где каждый кластер должен представлять отдельную производственную партию этих изделий, изготовленную из единой партии сырья) сводится к задаче разделения сферических гауссовых распределений. Задача выделения однородных партий электрорадиоизделий возникает, например, при комплектации узлов космических аппаратов. Специализированные тестовые центры проводят от нескольких десятков до нескольких сотен неразрушающих тестов [11; 12] для каждого экземпляра ЭРИ. При этом предполагается, что все экземпляры ЭРИ уже прошли входной контроль по ужесточенным нормам [13–16], т. е. отдельные их параметры могут колебаться лишь в очень узких диапазонах, определенных этими нормами, и отдельные параметры являются неинформативными. В то же время, совокупность большого числа этих параметров позволяет эффективно разделять производственные партии этих изделий.

В частности, хорошие результаты достигнуты при решении задачи автоматической группировки ЭРИ с использованием моделей k- средних, k- медиан и k- медоид. Недостатком одноименных алгоритмов, основанных на идее процедуры k- средних, называемой также процедурой Ллойда или ALA-процедурой [17; 18], а также PAM-алгоритма для задачи k- медоид является то, что они относятся к алгоритмам локального поиска (не в строгом смысле), зависящим от выбора начального решения. При этом разработаны детерминированные алгоритмы [19; 20], а также рандомизированные алгоритмы, обеспечивающие, тем не менее, весьма точный и при этом стабильный результат [21–23], что немаловажно во всех процедурах, связанных с космическим производством, все этапы которого требуют весьма строгой регламентации. В частности, хорошие результаты достигаются при применении кластеризации, основанной на расстояниях с прямоугольной метрикой [3].

Преимущество нечеткой кластеризации в виде задачи разделения смеси гауссовых распределений посредством EM-алгоритма заключается в том числе в том, что эта модель, в отличие от модели k -средних и аналогичных, оперирует не абстрактными расстояниями в неком пространстве характеристик различной физической природы, а вероятностными характеристиками возможности отнесения конкретного экземпляра ЭРИ к той или иной группе (кластеру).

При этом использование именно сферических гауссовых распределений позволяет в некотором смысле обратить так называемое проклятие размерности [24] в полезное свойство многомерных данных. Использование модели традиционных (не сферических) распределений N (ц, S ) с плотностью распределения

1 p ( x ) =-------------exp

(2 П n/2 E I

( x -ц ) T 2 ¹ ( x -ц )

,

где E- ковариационная (иначе - корреляционная) матрица, в случае использования данных очень большой размерности приводит к следующим эффектам. Во-первых, матрица размерности n для каждого гауссова распределения (т. е. для каждого кластера) требует достаточно много памяти и значительных вычислительных ресурсов при пересчете ЕМ-алгорит-мом на каждом шаге. Во-вторых, использование данной матрицы предполагает, что для каждой координаты каждое распределение (кластер) имеет собственное значение дисперсии (соответствующий элемент диагонали матрицы E), при этом плотность j-го распре- деления тем чувствительнее к изменению координаты, чем меньше дисперсия по этой координате. Таким образом, незначительные колебания какой-либо характеристики, вызванные, например, неточностью измерительных приборов, рассматриваются как значительные при принятии решения об отнесении объекта к тому или иному распределению (кластеру), снижая относительную значимость более информативных признаков.

Тот же эффект проявляется и при кластеризации с использованием модели k-средних в сочетании с нормировкой данных по среднеквадратичному отклонению или 0-1-нормировкой [4]. В то же время, использование специального метода нормировки исходных данных, учитывающего именно физическую природу каждой из характеристик ЭРИ [4], а не разброс характеристики в исследуемой партии изделий, позволяет добиться гораздо лучших результатов.

Аналогичным образом использование единого значения дисперсии по всем координатам (характеристикам), т. е. использование модели смеси сферических гауссовых распределений в сочетании со способом нормировки, описанным в [4], позволяет доби- ваться адекватных результатов при использовании данных очень большой размерности, которые являются результатом измерений, производимых в ходе тестирования ЭРИ.

Применение EM-алгоритма к задаче выделения однородных партий. EM-алгоритм для разделения смеси сферических распределений может быть описан следующим образом. Дан набор данных S с Rn, EM-алгоритм для смеси k нормальных распределений с общей сферической матрицей ковариации стартует с начальными стартовыми значениями параметров цi^ ai^ gi<0>, которые в дальнейшем обновляются в соответствии со следующей двухшаговой процедурой (здесь t – номер итерации).

Алгоритм 1 . EM-алгоритм.

Шаг 1. Пусть   Ti~ N(ц i(t >,g i(t> 2 In)   является плотностью i-го гауссова распределения: тi (x) =

=    1 f- x -ц/)

(2 n ) n / ² g n ^Xp ^     2 g i ’ ,

Для каждого вектора

исходных данных x e S и каждого 1 <  i <  k по формуле

Байеса [25] вычислим условную вероятность того, что x относится к i- му распределению с учетом текущих параметров:

P it ⁺¹\ ^x ) =

^aP ^т i ^{( x} ) Ea ? j ^x )

Шаг 2 . Производится адаптация параметров распределений. Пусть N – количество векторов данных:

«." *1’ = ^7 E p?*'^ x),(2)

N x e S

(t*1) _ ExeSxp*'(x)

Ц =    Na it *'    , g^*°2 = jE|x-Цit*'|2 pit+1>(x)(4)

^и x e S

Повторять с шага 1.

Условием останова в таком алгоритме является останов приращения целевой функции, в качестве которой принимается логарифмическая функция правдоподобия

k

L <*1'- = EE ln ( т - Р ?*^ x ) ) ■          (5)

x e S i =1

Мы использовали комбинированное условие останова: t > 100 или L ^{( t+} "  - L ⁽ t > < 0,0001.

Отметим, что в случае данных большой размерности ( d > 100) плотность отдельных распределений т i ( x ) может принимать как очень малые значения ( т i ( x ) < 1 • 10^-300), так и очень большие значения, что может потребовать применения специальных механизмов при реализации алгоритма. В частности, мы использовали библиотеку decimal [26], применение которой существенно замедляет расчеты, но обеспечивает работу с величинами требуемых порядков.

В работах [21–23] предложен подход к повышению точности и стабильности результата решения задач k- медиан, k- медоид, k- средних, основанный на применении жадных агломеративных эвристических процедур в комбинации с различными метаэвристиками и методами локального поиска. Идея жадной агломеративной эвристики основана на последовательном исключении кластеров из решения. Каждый раз удаляются те кластеры, удаление которых дает наименьший прирост целевой функции (данные задачи являются задачами минимизации).

В настоящей работе мы предлагаем аналогичные подходы к построению жадных агломеративных эвристических процедур. В данном случае мы имеем дело с задачей максимизации функции (5). Первые два подхода полностью аналогичны подходам, примененным в [21–23].

Алгоритм 2 . Жадная агломеративная эвристика, вариант 1.

Дано: начальное число гауссовых распределений (кластеров) k , требуемое число кластеров K .

1. Выбрать случайным образом начальное решение с K кластерами, т. е. выбрать случайным образом начальные параметры распределений множества рас-

пределений D = {N(цi0\ ci^2In), i = 1, k}. В качестве начальных значений цi<0> выбираются случайные векторы данных, дисперсии ci<0> рассчитываются по формуле (4). Также устанавливаются равные начальные значения множества весовых коэффициентов распре делений W = !а^0,i = 1,k\ = < —,...,—

I i ) I k k

• 2.    Выполнить алгоритм 1, получить новое (улучшенное) решение задачи, представленное множествами D и W .

• 3.    Если K = k , то останов.

• 4.    Для каждого i ' e { 1, K } выполнять следующее:

  • 4.1.    Получить усеченное множество распределений и множество их весовых коэффициентов D ‘ = D \ { N ( ц i ⁰ , c ^2 I n ) } , W ' = W \ { a i ^0> }.

• 4.2.    Следующая итерация цикла 4.

• 5.    Найти индекс i" = arg max L_r .

• 6.    Получить усеченные множества

Запустить алгоритм 1 с начальными значениями параметров распределений, представленных усеченным множеством D′ и весами W′ . При этом алгоритм 1 ограничивается одной итерацией. Для полученного ЕМ-алгоритмом решения рассчитать целевую функцию L согласно (5), сохранить ее значение в переменной L’ I’ .

i '=1, k

D = D \ { N ( ц i ^0>, c i '<⁰>² In ) } , W = W \ { a < ^0>}.

Перейти к шагу 3.

Кроме того, мы испытали два упрощенных алгоритма.

Алгоритм 3. Упрощенная жадная эвристика № 1.

Полностью повторяет алгоритм 2, кроме шага 4.2:

• 4. 2. Без запуска EM-алгоритма рассчитать целевую функцию L согласно (5), сохранить ее значение в переменной L′ _I′.

• 5. Найти индекс i " = arg max L i , .

Вычислительные эксперименты показывают, что если задать EM-алгоритму в качестве числа требуемых распределений (кластеров) значение k большее, чем фактическое количество кластеров в выборке, во многих случаях в результате работы алгоритма несколько «лишних» кластеров получают значение весовых коэффициентов w_i , близкое к нулю. На этом свойстве основана еще более упрощенная версия алгоритма.

Алгоритм 4 . Упрощенная жадная эвристика № 1. Частично повторяет алгоритм 2, при этом цикл 4–4.3 исключен, а шаг 5 выполняется в следующей редакции:

i '=1, k

Как и в работе о применении жадной агломера-тивной эвристики с алгоритмами k -средних [27], важным является вопрос выбора начального значения числа кластеров. В настоящей работе мы не рассматривали данный вопрос, ограничиваясь пока экспериментами с k = 2 K и k = 4 K (удвоенное и учетверенное число начальных кластеров).

Результаты вычислительных экспериментов. Результаты вычислительных экспериментов приведены для двух наборов данных. Первый набор – искусственно сгенерированный набор данных с m = 200, K = 3, n = 12. Второй набор – данные испытаний [28] электрорадиоизделий 1526ИЕ10 ( m = 3987, n = 205), нормированные согласно [4].

Сравнительные результаты работы алгоритмов представлены в табл. 1.

Из табл. 1 видно, что жадная эвристика (алгоритмы 2, 3 и 4) имеет преимущество перед использованием алгоритма 1 по точности результата. В то же время под вопросом остается оптимальное начальное количество кластеров k . Перспективным представляется исследование подхода с адаптацией начального количества кластеров, аналогичный подходу с адаптацией начального количества кластеров для решения задач k- средних и p- медианной задачи, описанному в [27].

Таблица 1

Сравнительные усредненные по 30 запускам результаты работы алгоритмов для двух наборов данных

Набор данных	Алгоритм	Усредненное значение целевой функции (5)	Среднее время работы, с
Сгенерированный набор дан-	Алгоритм 1	–7430,39	0,557
ных, m = 200, n = 12, K = 3	Алгоритм 2, k = 6	–7263,48	3,882
	Алгоритм 2, k = 12	–7028,99*	21,472
	Алгоритм 3, k = 6	–7230,06	3,913
	Алгоритм 3, k = 12	–7036,80	23,581
	Алгоритм 4, k = 6	–7152,64	2,932
	Алгоритм 4, k = 12	–7110,28	9,820
Испытания ЭРИ 1526ИЕ10,	Алгоритм 1	613261,510	14,820
m = 3987, n = 205, K = 3	Алгоритм 2, k = 6	622559,536*	113,140
	Алгоритм 2, k = 12	622559,536*	653,113
	Алгоритм 3, k = 6	622559,536*	96,677
	Алгоритм 3, k = 12	622559,536*	667,399
	Алгоритм 4, k = 6	622559,536*	96,677
	Алгоритм 4, k = 12	613506,5485	553,159

Примечание: * – лучший результат.

Таблица 2

Фрагмент решения задачи автоматической группировки результатов испытаний ЭРИ 1526ИЕ10, m = 3987, n = 205, K = 3

№ вектора данных (№ ЭРИ)	Предполагаемый номер кластера	Вероятность отнесения к предполагаемому кластеру
225	1	1
226	1	1
227	1	1
230	2	0,87564
231	1	0,99554
232	1	1

Фрагмент итоговых результатов с указанием оценки вероятности отнесения векторов данных к тому или иному распределению (кластеру) показан в табл. 2. Видно, что в случае многомерных данных вероятности стремятся к 0 или 1, что подтверждает гипотезу о том, что данные являются с -разделенными при малых значениях с.

Заключение. Таким образом, вычислительные эксперименты показывают, что применение жадной агломеративной эвристики позволяет получить результаты значительно более высокой точности в сравнении с мультистартом EM-алгоритма из случайных начальных решений. При этом самая простая и самая быстрая модификация алгоритма с жадной эвристикой – алгоритм 4 – не уступает по точности результатов другим модификациям, требующим гораздо более значительного времени счета. Программное обеспечение на основе описанного подхода может быть использовано в реализации задач повышения надежности программно-аппаратных комплексов автоматизированных систем управления в части управления качеством выпускаемой продукции.

Сходство ЕМ-алгоритма с алгоритмами для решения задач k- средних, k- медоид и k- медиан, а также сходство соответствующих алгоритмов, реализующих жадную агломеративную эвристику, дает обоснованную надежду на получение в дальнейшем алгоритмов, обеспечивающих еще более высокую точность и стабильность результата.