Выявление стеганографических вложений в WAV-файлах с помощью спектрального анализа

Введение. Постановка задачи

Звуковые WAV-файлы порой используют в качестве контейнеров для скрытой передачи информации. Кроме того, приемы стеганографии используются для создания меток, подтверждающих авторство музыкальных произведений. Внедрение информации можно осуществлять в два последних (младших) разряда цифровой выборки. Экспертная оценка показала, что обнаружить на слух такие вложения невозможно [1]. В большинстве случаев внедрение скрытой информации в WAV-файлы происходит по всей длине файла, включая участки относительной тишины.

Рис. 1. Звуковой сигнал с участком тишины

На участке mn , изображенном на рис. 1, звук либо совсем отсутствует («полная тишина»), либо его уровень незначителен. С точки зрения криптоанализа – это наиболее уязвимый участок фонограммы. Такой участок появляется в паузах между воспроизведением музыкальных произведений, в радиорепортажах, радиоспектаклях, звуковых книгах и т.д. Можно попытаться обнаружить имеющееся скрытое вложение, анализируя спектр сигнала в местах «полной тишины».

Спектральный анализ сигналов

Для определения возможности обнаружения вложений были исследованы типичные звуковые сигналы, сигналы шумов и сигналы стеганографических вложений. При этом вложения исследовались только в зоне «полной тишины». Стеганографические вложения осуществлялись путем замены младшего бита цифрового отсчета (метод LSB).

Пример сигнала «полной тишины» со сделанным внедрением в шестнадцатый разряд тринадцати отсчетов (восьми единиц и пяти нулей) показан на рис. 2, где приняты обозначения: А – амплитуда сигнала в мкВ, t – время в С, и показан типичный сигнал вложения, который имел частоту дискретизации 44100 Гц и уровень квантования 16 бит.

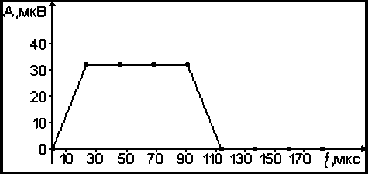
Рис. 2. Трапецеидальный сигнал

Спектральные плотности непериодических сигналов вложений, звуковых сигналов и сигналов шума вычислялись с помощью интеграла Фурье [2]:

co — ■ t

F^ = \fW   dt ,       (1)

— co где co – частота (рад/С). Дискретные спектры периодических сигналов вложений, звуковых сигналов и сигналов шума были найдены с помощью ряда Фурье [4]:

2 ^       - ico, t

^Fk⁼FVfW   ^k dt ^;         (2)

* 0

“k^=k^ ^,                 (3)

где T – период; к – номер гармоники, ®k – частота гармоники, рад/С; F^ – амплитуда гармоники, В. Все расчеты выполнялись в математической системе Mathcad 14.

Таблица 1. Непериодические трапецеидальные импульсы

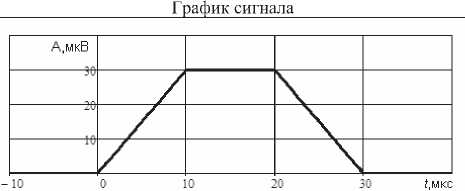
Спектральная плотность b ,мкЬс--------------------------------

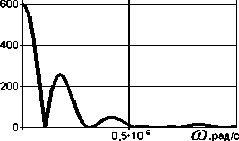
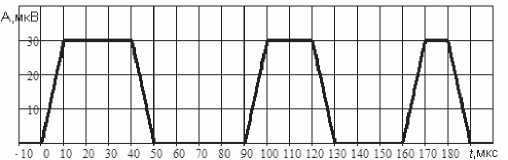
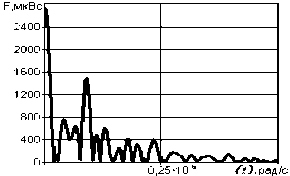
Таблица 2. Периодические трапецеидальные импульсы

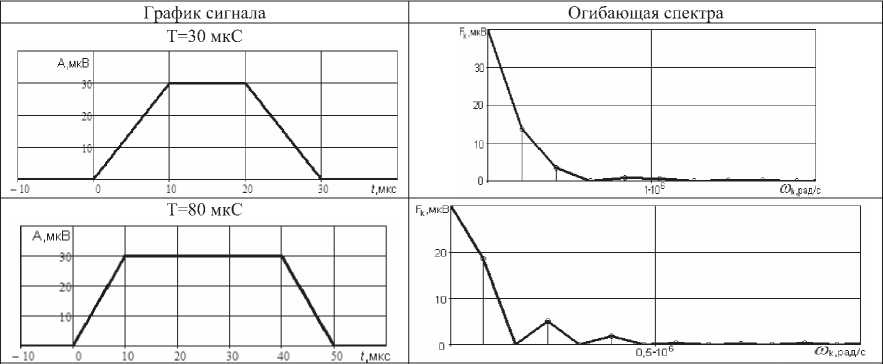
Таблица 3. Спектр непериодического шума

График сигнала								Спектральная плотность
								Р.мВс-----	--
А.мВ---				-—=				120--
0,75-- 0,50--								эоД---
0,25-/			—					60 \Л
о*—	20	40	60    80	100	120	140	160 Г. МКС	"ft	0.125-1 о"	<У,рад/с
А,мВ —				------г				120- ----	—
1,5— 1,0— 0,5 —	—		=-—==			—X		90--- 60 iA	—
0^	20	40	60     80	100	120	140	160 Lmkc		0.125-10s	<У,рад/с

Таблица 4. Спектр периодического шума

График сигнала

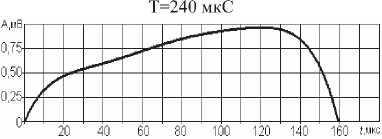
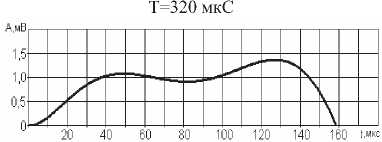
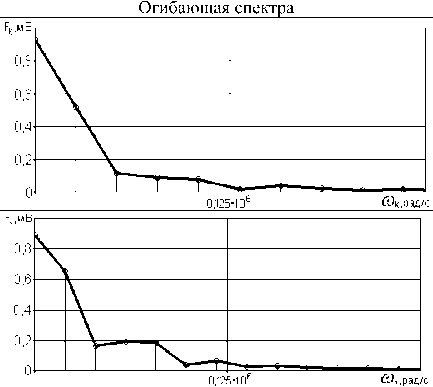
Таблица 5. Спектр непериодических звуковых сигналов

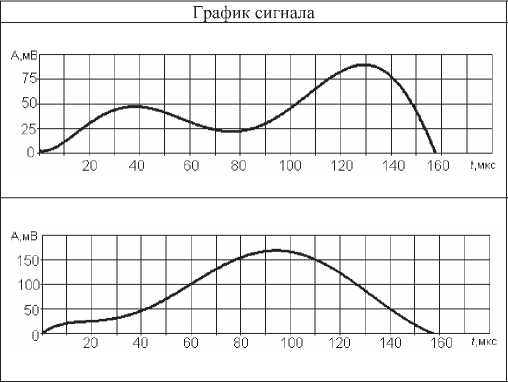
Спектральная плотность

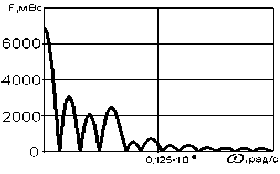
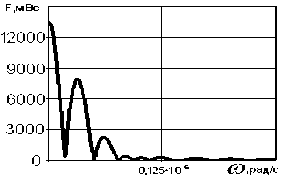
Таблица 6. Спектр периодических звуковых сигналов

Г рафик сигнала

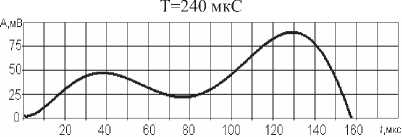
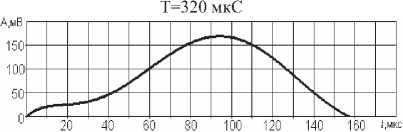
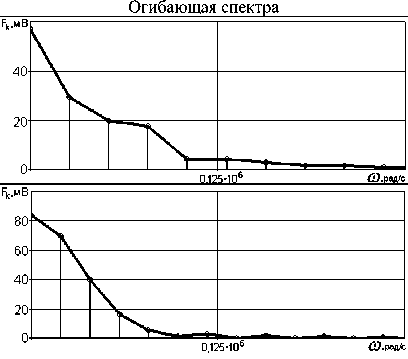
Спектральные плотности непериодических импульсных трапецеидальных сигналов и их форма представлены в таблице 1, методика расчета в [3]. Результаты расчета спектра периодических трапецеидальных сигналов с различной скважностью сведены в таблицу 2. При расчете спектров сигналов шума и звуковых сигналов они были аппроксимированы с необходимой точностью с помощью программы TableCurve 2D [4].

Спектральные плотности некоторых непериодических сигналов шума представлены в таблице 3, а спектры периодических сигналов шума – в таблице 4.

Дискретный спектр типичных звуковых непериодических сигналов представлен в таблице 5, а спектр

Таблица 7. Параметры спектра периодических сигналов – в таблице 6. Приведенные спектрограммы позволяют визуально оценить сходство и различия спектров сигналов. Для их количественного сравнения рассчитывались следующие числовые параметры (см. таблицу 7): максимальное значение спектральной плотности; ширина спектра; максимальная скорость затухания спектра; площадь под огибающей спектра. Максимальное значение спектральной плотности вычислялась по формуле (2) при к = О.

Ширина спектра трапецеидальных сигналов определялась по граничной частоте первого лепестка спектра. Для всех остальных

Параметры Трапецеидальный сигнал Шум Звуковой сигнал 1 2 1 2 1 2 Максимальное значение спектральной плотности 10"3 В 0,04 0,03 0,9275 0,8917 57 84 Ширина спектра 106 рад/С 0,62 0,32 0,0262 0,0196 0,0262 0,0196 Максимальная ско-эость затухания 10"" ВС/рад -1,75 -1,91 -198,9 -150,01 -8699 -18860 Площадь под огибающей спектра В рад/С 9,4 4,8 43,0271 50,53 2882 4530 сигналов определялась по частоте, которая дает 90% от общей площади фигуры энергетического спектра.

Для вычисления максимальной скорости затухания график огибающей спектра был аппроксимирован адекватной функцией /(.со) . Скорость затухания вычислялась с помощью первой про-

Q п п , , df^ изводной dco

.

Максимальная скорость рассчитывалась в точке перегиба функции. Точка перегиба определялась из уравнения (Л(су) _^ Площадь под огиба-dco ющей спектральной плотности вычислялась как

s(co) = yXco^dro. О

В результате проведенного анализа было установлено следующее:

• -    все рассчитанные параметры (см. таблицу 7) позволяют надежно отделить сигнал вложения от звукового сигнала и сигнала шума;

• -    ширина спектра трапецеидального сигнала на порядок превосходит ширину спектра звукового сигнала;

• -    максимальная скорость затухания спектра звукового сигнала на четыре порядка выше максимальной скорости затухания спектра трапецеидального сигнала;

• -    площадь под огибающей спектра звукового сигнала на четыре порядка больше площади под огибающей спектра трапецеидального сигнала;

• -    сигнал шума по всем параметрам занимает промежуточное положение между звуковым сигналом и трапецеидальным сигналом вложения.

Выводы

Проведенные исследования показали, что наиболее уязвимым местом фонограммы является участок с «полной тишиной». По этой причине разработчики алгоритмов внедрения (криптографы) не должны использовать эти участки фо- нограммы для внедрения скрытой информации, а криптоаналитики, наоборот, внимательно исследовать их.

Сопоставление спектров трапецеидальных сигналов и спектров типичных звуковых фрагментов фонограммы показывает принципиальную возможность обнаружения стеганографических вложений на участках с «полной тишиной» с помощью всех рассчитанных параметров