Выявление зависимости между аэродинамическими условиями и конфигурацией одиночного здания

Цитирование: Вдовина Е. В. Выявление зависимости между аэродинамическими условиями и конфигурацией одиночного здания / Е. В. Вдовина, С. С. Добросмыслов. Журн. Сиб. федер. ун-та. Техника и технологии, 2023, 16(5). С. 619–634. EDN: GRDMNA следовании Поддаевой О. И., где приведена методология проведения эксперимента и сравнение с расчетными аэродинамическими коэффициентами [4].

Наиболее распространен третий метод исследований – математический, с использованием программных комплексов. Для задач аэродинамики рассматриваются ламинарный и турбулентный потоки, с решением уравнений Навье-Стокса и Рейнольдса. Данную задачу можно решить в разных программных комплексах, таких как: Autodesk Flow Design [5, 6], ANSYS [7, 8, 9], SigmaFlow [1], ENVI-met [10,11] и Star-CCm+ [12].

По объекту исследования работы в данной области можно разделить на изучение одиночных зданий и квартальной застройки. Одиночные здания рассматриваются при вариации одного из параметров: геометрических размеров [6], высоты здания [5], угла поворота относительно преобладающего потока [4], а далее выявляются изменения ветрового давления, аэродинамических коэффициентов и формы, структуры потока.

Квартальные застройки рассматриваются или уже для существующих кварталов [1, 7, 10, 12] для выведения рекомендаций по улучшению экологической безопасности, или изучаются элементарные модели застроек для выявления аэродинамических закономерностей [9, 11].

Стоит отметить, что при проектировании квартала для установления расстояния между объектами руководствуются требованиями инсоляции и пожаробезопасности. К сожалению, упоминание о ветровом комфорте в отечественной нормативной литературе отсутствует. В зарубежных нормативах расчет ветрового комфорта обязателен при проектировании кварталов в Европейских странах, Японии и Америке. В Нидерландах приняты немецкие нормы NEN 8100, в Америке используются нормы, основанные на исследованиях Т. В. Лоусона, а в Японии используются нормы, разработанные А.Ф.Е Вайсом и А. Д. Пендварденом. Их объединяют значения, что при скорости ветра более 5 м/с ветровой комфорт не обеспечивается. Нижняя граница варьируется от 0,4–2,5 м/с [8].

В промышленном городе Красноярске, в силу географических особенностей и плотной застройки города, наблюдаются низкие скорости ветра и, как следствие, регулярное превышение уровня предельно допустимых концентраций (ПДК). Экологическую проблему качества атмосферного воздуха требуется решать комплексно, поэтому со стороны строительной сферы требуется подобрать оптимальную конфигурацию зданий, которая бы обеспечила наилучшие аэродинамические условия.

Целью исследования являлось установление зависимости между аэродинамическими условиями, которые описываются областью отрицательного давления, и областью низких скоростей ветра, а именно потоков со скоростью менее 1,2 м/с. Требовалось установить приоритетность факторов на формирование зон застоя, найти корреляционную связь между оценочными характеристиками и подобрать оптимальные значения параметров здания в условиях ветрового режима г. Красноярска.

Методология исследования

В качестве объекта исследования было выбрано одиночное здание как элементарная единица застройки. В ходе исследования изменялись следующие параметры:

– Этажность (9–14–18–25 этажей);

– Угол поворота здания относительно потока (0˚– 30˚ – 45˚ – 60˚ – 90˚);

– Ширина здания (12–15–18–21 м);

– Длина здания, которая варьируется от длины секции (30–60–90 м).

Исследования велись с применением математического моделирования с использованием программного комплекса COMSOL Multiphysics, который выполняет расчеты, основанные на уравнении массопереноса методом конечных элементов.

Для корреляционно-регрессионного анализа полученных данных применяется программа Statistica SR. Данный софт позволяет вывести уравнение регрессии и коррелировать полученные зависимости в поисках оптимальных параметров жилой застройки.

Математическая модель

Ветровой поток рассматривается как движение несжимаемой жидкости и описывается системой дифференциальных уравнений Навье-Стокса.

Общий вид уравнения Навье-Стокса (1):

р(и ■ V)u = V[— pl + (77 + p_T)(Vu + (Vu)^T)] + F, Vu = 0.

Решение уравнения Навье-Стокса осуществлялось в рамках приближения k-έ (2):

puVk = V[j] + C'^l7a_T)Vk\ + т7т^(Ю - P^£.

РИМЕ = V (т? + 'VdJ^ +---7---7— к         к

Уи

р(и) = (vTTTw): Чг = pCllk2,E'

где p - давление, Pa; F - поле внешних сил; е - энергия, Дж; Н/м³; к - кинетическая энергия объема, Дж/м³; C, g - коэффициент, учитывающий диффузию энергии; п, П г - динамическая и турбулентная вязкость, Па ∙ c;

Математическая модель турбулентного движения воздуха реализована в программном комплексе COMSOL Multiphysics со следующими исходными данными:

– Общие размеры модели АхВхН = 200х200х200 м;

• –    Размер сетки – нормальный;

• –    Скорость ветра = 2,5 м/с – среднегодовая скорость ветра в г. Красноярске;

• –    Используемые материалы: воздух, ячеистый бетон;

• –    Тип расчета – стационарный.

Анализ результатов исследования

Выполнен расчет 180 вариаций моделей одиночного здания следующих площадей: 30х12 м, 30х15 м, 30х18 м, 30х21 м, 60х12 м, 60х15 м, 60х18 м, 60х21 м, 90х18 м. Для каждого варианта площади было 4 варианта высоты здания и 5 вариантов угла поворота. Для определения ветровой тени выводился объем области скорости ветра менее 1,2 м/с, что соответствует 1 баллу по шкале Бофорта. Для определения аэродинамической тени выводился объем зоны отрицательного давления (p <0). Графические результаты моделирования представлены на рис. 1–4.

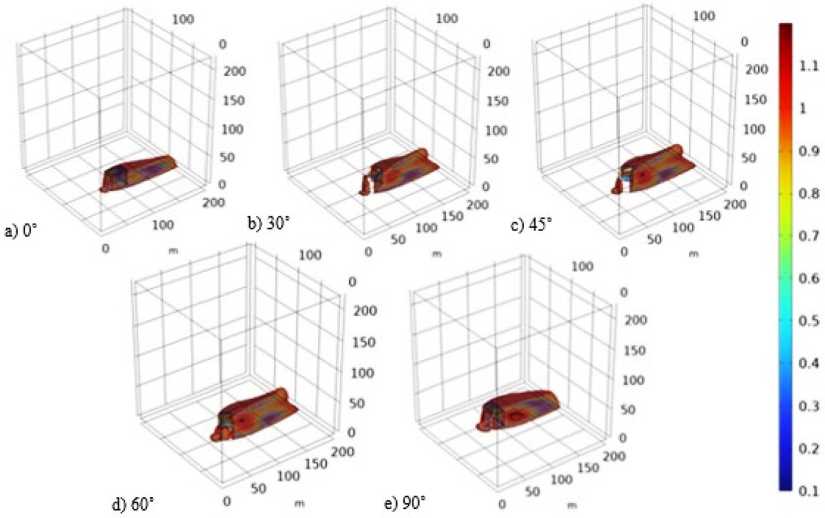
Рис. 1. Область низких скоростей ветра при изменении угла поворота здания с площадью S =30х18 м и высотой H = 27 м, м/с

Fig. 1 – Low-speed velocity field at different angles of rotation for a single building with an area of S = 30x18 m and a height of H = 27 m, m/s

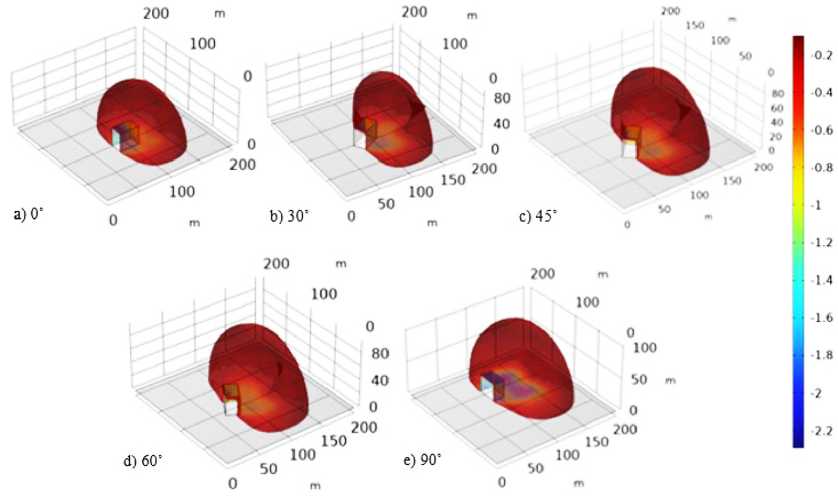
Рис. 2. Область отрицательного давления за зданием с площадью S = 30х18 м и высотой H =27 м, Па

Fig. 2. Negative pressure area behind a single building with S = 30x18 m and a height of H = 27 m, Pa

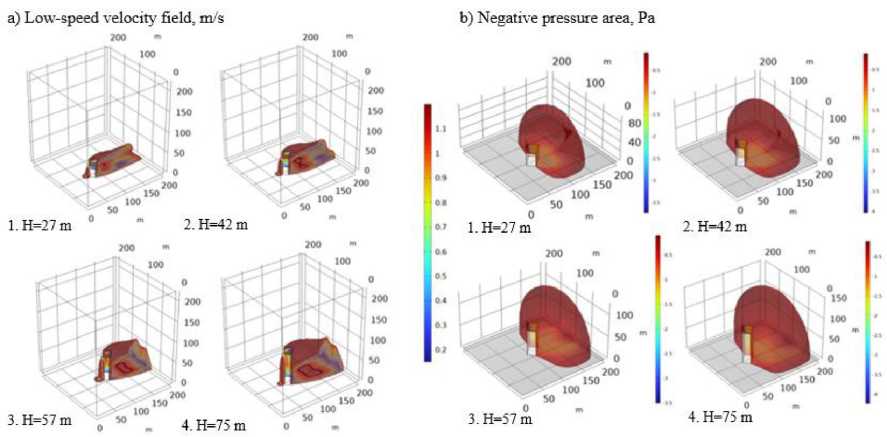
Рис. 3. Графические результаты одиночного здания площадью S = 30x18 м и α=45⁰

Fig. 3. Graphical results of a single building with an area of S = 30x18 m and α=45⁰

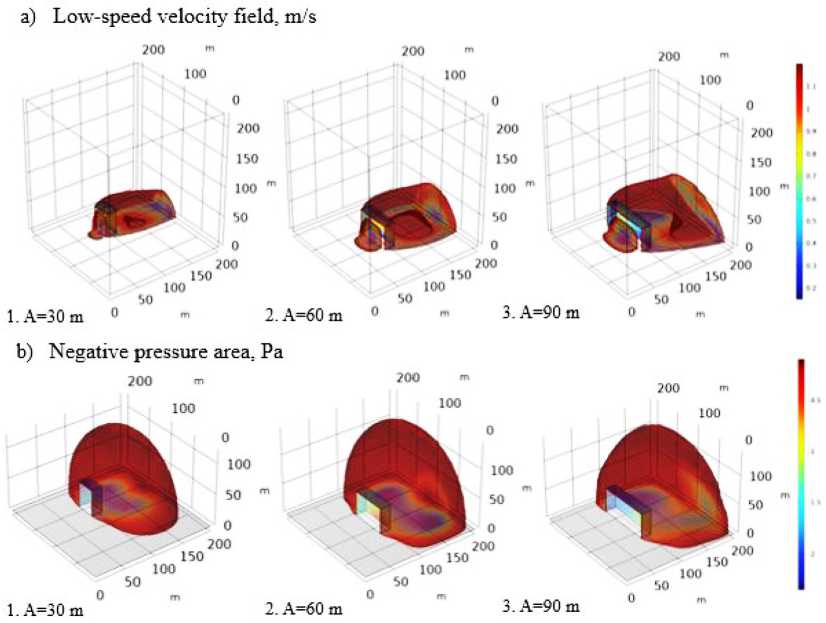
Рис. 4. Графические результаты одиночного здания шириной В=18м, высотой Н=42м и α=90⁰

Fig. 4. Graphical results of a single building with width B=18m, height H=42m and α=90⁰

На качественном уровне наблюдается тенденция увеличения каждой характеристики зоны застоя с увеличением высоты здания и угла поворота. На данном этапе анализа отмечается, что отношение области низких скоростей ветра к области отрицательного давления варьируется от 0,13–0,24.

Корреляционно-регрессионный анализ

Для получения математического выражения размеров зоны застоя от параметров одиночного здания применен корреляционно-регрессионный анализ. Для многофакторной корреляционной модели объема области низких скоростей ветра ( у ) подобраны следующие факторы, которые оказывают наиболее существенное влияние на ее уровень: А ( x ₁) – длина здания, м; В ( x ₂) – ширина здания, м; Н ( x ₃) – высота здания, м; α ( x ₄) – угол поворота относительно преобладающего потока, ˚. Данные факторы не имеют функциональной связи. Произведем отбор влиятельных значений, представленный на рис. 5.

Путем визуального анализа ранжированного ряда значения не имеют существенного отклонения, следовательно, соответствуют закону нормального распределения.

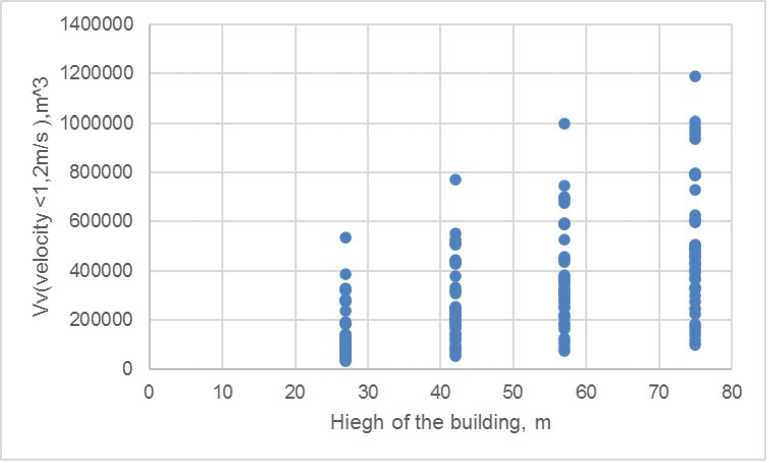
Рис. 5. Анализ влиятельных значений области низких скоростей ветра от высоты здания

Fig. 5. Analysis of the influential values of the low-speed velocity field from the height of the building

В данном случае трудно обосновать форму зависимости между результативными и факторными показателями, поэтому рассматривалось три вида линейной регрессии: множественная, факторная и полиномная [13, 14]. В табл. 1 представлены результаты проверки гипотезы об адекватности модели для области низких скоростей ветра.

Все модели имеют весьма высокие коэффициенты корреляции и детерминации. Наиточнейшие показатели у факторной модели, но есть неудобство в виде 15 степеней свободы дисперсии. Так как объемная формула затруднит расчет, а разница между множественной и по-линомной моделями незначительна, предпочтение отдано множественной модели регрессии. Тогда запись зависимости имеет следующий вид:

у = b 0 + b 1 ∙ х 1 + b 2 ∙ х 2 + b 3 ∙ х 3 + b 4 ∙ х 4 , (3) где выборочные коэффициенты b 0 , b 1 , b 2 , b 3 , b 4 – это оценки соответствующих коэффициентов уравнения регрессии, характеризующего всю генеральную совокупность.

Для описания влияния факторных признаков на размер ветровой тени построена регрессионная модель. Используя программу Statistica, проведем дисперсный анализ, выведем коэффициенты регрессии, а для определения значимости и приоритетности факторов выведем коэффициенты корреляции.

Анализируя показатели регрессионной статистики, можно сделать вывод, что нескорректированный коэффициент множественной детерминации и множественный коэффициент корреляции указывают на высокую (более 85 %) предопределенность результата Y в построенной регрессионной модели рассматриваемыми факторными признаками. Показатели дисперсионного анализа представлены в табл. 3.

Таблица 1. Проверка гипотезы об адекватности модели области низких скоростей ветра

Table 1. Testing the hypothesis of the adequacy of the model of the low-speed velocity field

Вид регрессии	Множественный R	R-квадрат	Скорректированный R-квадрат	df	F	p
Множественная	0,9053	0,8196	0,8155	4	198	0,00
Факторная	0,9898	0,9798	0,9779	15	530	0,00
Полиномная	0,9081	0,8247	0,8165	8	100	0,00

Таблица 2. Показатели регрессионной статистики для области низких скоростей ветра

Table 2. Regression statistics indicators for the low-speed velocity field

Показатель	Значение показателя
Множественный R	0,9053
R-квадрат	0,8197
Скорректированный R-квадрат	0,8155
Стандартная ошибка оценки	7925933 ∙ 106
Наблюдения	180

Таблица 3. Показатели дисперсионного анализа для области низких скоростей ветра

Table 3. Indicators of variance analysis for the low-speed velocity field

Показатель	Степени свободы	Сумма квадратов	Средний квадрат	F	F кр	Значимость
Регрессия	4	7925933 ∙ 106	1981483 ∙ 106	198,83	5,63	0,00
Остаток	175	1743939 ∙ 106	9965366 ∙ 103
Всего	179	9669872 ∙ 106

Анализируя показатели дисперсионного анализа, можно сделать вывод о том, что уравнение множественной регрессии и коэффициент множественной детерминации статистически значимы, что подтверждено F-критерием Фишера, так как F ф > F_кр. Показатели регрессионного и корреляционного анализов приведены в табл. 4 и 5.

Таблица 4. Показатели регрессионного анализа для области низких скоростей ветра

Table 4. Regression analysis indicators for the low-speed velocity field

Фактор	Коэффициенты B	Стандартная ошибка	t-статистика	P-значение
Y-пересечение	-537195	48374	-11,11	0,00
X 1	4399	374,07	11,76	0,00
X 2	4251	2339,97	1,82	0,07
X 3	7304	418,11	17,47	0,00
X 4	4590	248,02	18,51	0,00

Таблица 5. Корреляционный анализ для области низких скоростей ветра

Table 5. Correlation analysis for the low-speed velocity field

Фактор	А, м	В, м	Н, м	α, °	Vv, м3
А, м	1,000000	0,104257	0,000000	0,000000	0,385700
В, м	0,104257	1,000000	0,000000	0,000000	0,098216
Н, м	0,000000	0,000000	1,000000	-0,000000	0,560809
α, °	0,000000	0,000000	-0,000000	1,000000	0,594121
Vv, м3	0,385700	0,098216	0,560809	0,594121	1,000000

Анализируя показатели регрессионного анализа, можно сделать вывод, что величина, оценивающая агрегированное влияние прочих факторов на результативный показатель, и коэффициенты регрессии b1, b3, b4 статистически значимы, что подтверждается t-критерием Стьюдента, равным 2,776, а коэффициент регрессии b2 не удовлетворяет требованиям. Исходя из корреляционного анализа на область низких скоростей ветра наиболее значимым фактором является угол поворота относительно преобладающего потока, вторым по значимости – высота здания, третьим – длина здания. Фактор ширины здания не является статически значимым. Вероятность для рассматриваемых факторных признаков не превышает принятый уровень, что подтверждается показателем вероятности случайных значений параметров регрессии. Уравнение множественной регрессии области низких скоростей ветра имеет вид у = –537195 + 4399 ∙ А + 7304 ∙ Н + 4590 ∙ α. (4)

Для многофакторной корреляционной модели объема отрицательного давления ( у ) подобраны те же факторы, что и области низких скоростей ветра. Произведем отбор влиятельных значений, представленный на рис. 6.

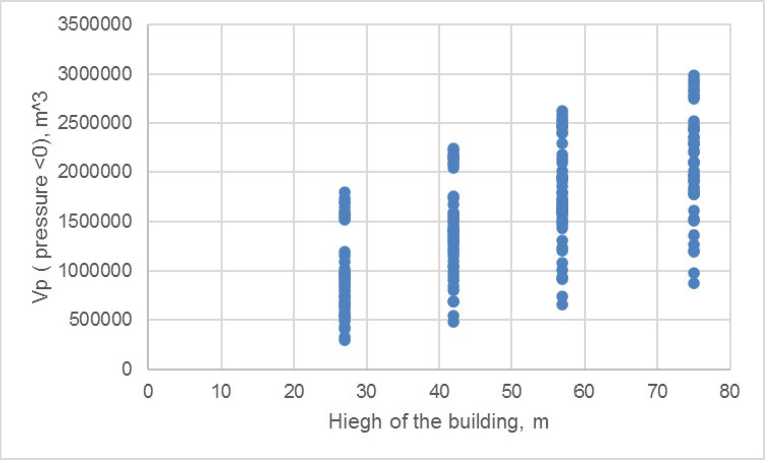
Рис. 6. Анализ влиятельных значений области отрицательного давления от высоты здания

Fig. 6. Analysis of the influential values of the negative pressure area from the height of the building

Таблица 6. Проверка гипотезы об адекватности модели области отрицательного давления

Table 6. Testing the hypothesis of the adequacy of the model of the negative pressure area

Вид регрессии	Множественный R	R-квадрат	Скорректированный R-квадрат	df	F	p
Множественная	0,8939	0,7990	0,7944	4	173	0,00
Факторная	0,9230	0,8520	0,8384	15	63	0,00
Полиномная	0,9251	0,8559	0,8491	8	126	0,00

В табл. 6 представлены результаты проверки гипотезы адекватности модели для области отрицательного давления.

Для модели области отрицательного давления выбрана полиномная модель, так как у нее самые высокие показатели коэффициентов. Тогда запись зависимости имеет следующий вид (5):

у = b 0 + b 1 ∙ х 1 + b 2 ∙ х 1 ² + b 3 ∙ х 2 + b 4 ∙ х 2 ² + b 5 ∙ х 3 +

+ b 6 ∙ х 3 ² + b 7 ∙ х 4 + b 8 ∙ х 4 ²,                                                            (5)

где выборочные коэффициенты b 0 , b 1 , b 2 , b 3 , b 4, b 5 , b 6 , b 7 , b 8 – это оценки соответствующих коэффициентов уравнения регрессии.

Для описания влияния факторных признаков на размер области отрицательного давления построена регрессионная модель.

Нескорректированный коэффициент множественной детерминации и множественный коэффициент корреляции указывают на высокую (более 85 %) предопределенность результата Y в построенной регрессионной модели рассматриваемыми факторными признаками. Показатели дисперсионного анализа для модели области отрицательного давления представлены в табл. 8.

Следовательно, уравнение множественной регрессии и коэффициент множественной детерминации статистически значимы, что подтверждено F-критерием Фишера [13], так как F ф > F_кр. Показатели регрессионного и корреляционного анализов приведены в табл. 9 и 10.

Анализируя показатели регрессионного анализа, можно сделать вывод, что коэффициенты регрессии b₁, b₂, b₅, b₆, b₇, b₈ статистически значимы, что подтверждается t-критерием Стьюдента, а коэффициенты регрессии b 3, b 4 не удовлетворяют требованиям. Исходя из корреляционного анализа на область низких скоростей ветра наиболее влиятельным фактором служит

Таблица 7. Показатели регрессионной статистики для области отрицательного давления

Table 7. Regression statistics indicators for the negative pressure area

Показатель	Значение показателя
Множественный R	0,9251
R-квадрат	0,8559
Скорректированный R-квадрат	0,8491
Стандартная ошибка оценки	6632471 ∙ 107
Наблюдения	180

Таблица 8. Показатели дисперсионного анализа для области отрицательного давления

Table 8. Indicators of variance analysis for the negative pressure area

Показатель	Степени свободы	Сумма квадратов	Средний квадрат	F	F кр	Значимость
Регрессия	8	6632471 ∙ 107	8290589 ∙ 106	126,9	5,63	0,00
Остаток	171	1117027 ∙ 107	6532323 ∙ 104
Всего	179	7749498 ∙ 106

Таблица 9. Показатели регрессионного анализа для области отрицательного давления

Table 9. Regression analysis indicators for the negative pressure area

Фактор	Коэффициенты B	Стандартная ошибка	t-статистика	P-значение
Y-пересечение	-2647220	655764	-4,036	<0,001
X 1	33712	5438	6,198	0,000
X 2	-235	49,2	-4,781	<0,001
X 3	89407	74332,1	1,203	0,231
X 4	-1919	2245,1	-0,855	0,394
X 5	40515	7598,8	5,332	0,000
X 6	-167	73,5	-2,869	0,025
X 7	23949	1964,6	12,190	0,000
X 8	-130	20,7	-6,274	0,000

Таблица 10. Корреляционный анализ для области отрицательного давления

Table 10. Correlation analysis for the negative pressure area

Фактор А, м А2, м2 В, м В2, м2 Н, м Н2, м2 α, ° α2 Vр, м3 А, м 1,000 0,984 0,104 0,085 0,000 -0,000 0,000 0,000 0,258 А2, м2 0,984 1,000 0,121 0,099 0,000 -0,000 0,000 0,000 0,232 В, м 0,104 0,121 1,000 0,996 0,000 -0,000 0,000 0,000 0,138 В2, м2 0,085 0,099 0,996 1,000 0,000 -0,000 0,000 0,000 0,134 Н, м 0,000 0,000 0,000 0,000 1,000 0,990 -0,000 -0,000 0,636 Н2, м2 -0,000 -0,000 -0,000 -0,000 0,990 1,000 -0,000 -0,000 0,620 α, ° 0,000 0,000 0,000 0,000 -0,000 -0,000 1,000 0,946 0,562 α2 0,000 0,000 0,000 0,000 -0,000 -0,000 0,946 1,000 0,473 Vр, м3 0,258 0,232 0,138 0,134 0,636 0,620 0,562 0,473 1,000 высота здания, вторым по значимости является угол поворота, третьим – длина здания. Фактор ширины здания не является статически значимым. Вероятность для рассматриваемых факторных признаков не превышает принятый уровень, что подтверждается показателем вероятности случайных значений параметров регрессии.

Уравнение полиномной регрессии области отрицательного давления ветра имеет вид у = –2647220 + 33716 ∙ А – 235 ∙ А2 + 40545 ∙ Н –

– 167 ∙ Н2 + 23949 ∙ α – 130 ∙ α2.                                                (6)

Вывод оптимальных параметров здания

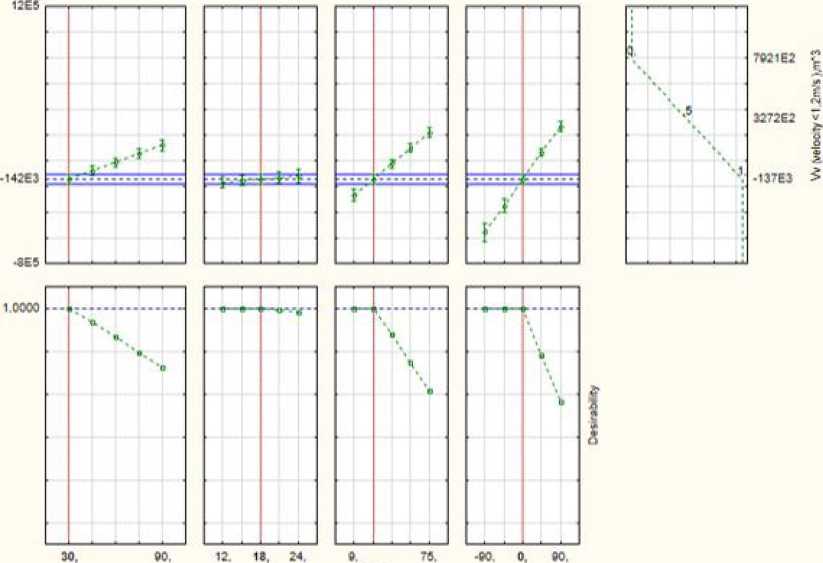
На рис. 7 отображены результаты корреляционно-регрессионного анализа и подобраны оптимальные параметры здания по области низких скоростей ветра.

При анализе профилей желательности выявлено, что наиболее оптимальный вариант относительно размера области низких скоростей ветра – одиночное здание площадью 30х18 м, высотой в 8 этажей, расположенное под углом 0˚ к преобладающему потоку, в условиях ветрового режима г. Красноярска.

Стоит отметить, что при высоте здания в 3–8 этажей показатели области низких скоростей ветра практически не изменны, далее наблюдается резкий рост значений. Оптимальная ширина здания варьируется от 12 до 18 м. При увеличении высоты и угла поворота здания размеры нежелательной ветровой тени также увеличиваются. На рис. 8 представлены профили относительно области отрицательного давления.

Основываясь на профилях прогнозируемых значений для области отрицательного значения, можно утверждать, что наиболее влиятельный фактор для зоны отрицательного давления – этажность здания. Чем ниже здание, тем меньше зона застоя. Зависимости параметров имеют криволинейный характер, в отличие от зависимостей области низких скоростей ветра, в силу формы уравнения регрессии. Относительно области отрицательного давления наиболее экологичной является трехэтажное здание площадью 30х15 м, расположенное под углом в 45˚ относительно преобладающего потока.

Profiles for Predicted Values and Desirability

Length fax m               VHd!h(b),m          HghtfH}, tn              Angle                      Desmrir/

25,6

Рис. 7. Профиль прогнозируемых значений и желательности для области низких скоростей ветра

Fig. 7. The profile of predicted values and desirability for the low-speed velocity field

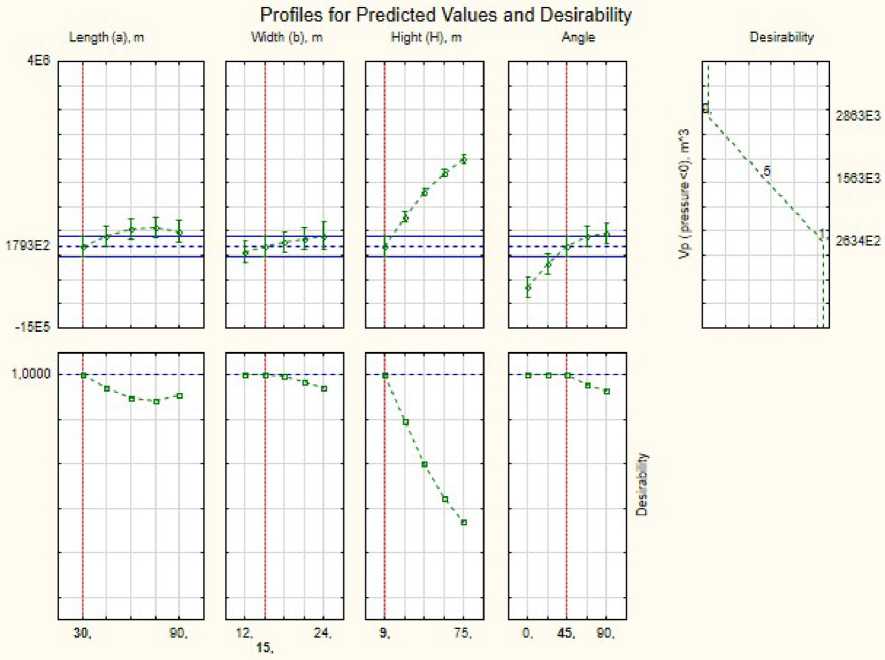
Рис. 8. Профиль прогнозируемых значений и желательности для области отрицательного давления

Fig. 8. The profile of predicted values and desirability for the negative pressure area

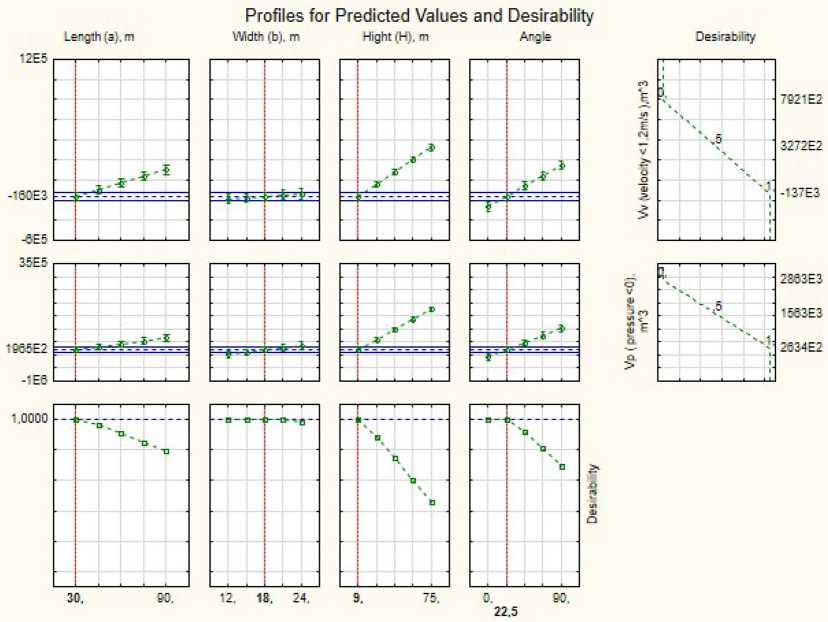
Рис. 9. Профиль прогнозируемых значений и желательности для зоны застоя

Fig. 9. The profile of predicted values and desirability for the stagnation zone

При совмещении двух характеристик зоны застоя были получены следующие профили, представленные на рис. 9.

При визуальном анализе профилей прогнозируемых значений определено, что наиболее влиятельные параметры – высота и угол поворота здания, что не противоречит вышесказанным выводам.

Итак, в условиях ветрового режима города Красноярска наиболее экологичное объемнопланировочное решение для одиночного здания – здание высотой 9 м, площадью 30х18 м, под углом 22,5˚ к преобладающему потоку.

Выводы

По результатам проведенного исследования была выявлена зависимость между параметрами одиночного здания и аэродинамическими условиями, описанными в виде области недопустимо низких скоростей ветра и области отрицательного давления. Установлено соотношение между двумя характеристиками. Полученные уравнения регрессии являются статистически значимыми, следовательно, могут применяться на практике с целью подбора наиболее экологичных объемно-планировочных решений здания на предпроектной стадии согласования. Определено, что наиболее влиятельными параметрами на зону застоя считаются высота здания и угол его поворота относительно преобладающего потока. Полученные оптимальные параметры здания констатируют, что для улучшения экологической обстановки в городе Красноярске следует снизить этажность до 3–8 этажей и тщательней продумывать расположение здания в плане.