Вынужденные колебания консольной балки с массой и упруго закрепленным концом

В работе исследуются вынужденные колебания консольной балки Эйлера-Бернулли с массой и с упруго закрепленным концом с применением техники обобщенных функций. Данная модель рассматривалась в работе [1], где применялся подход, связанный с разложением решения задачи в ряд Фурье по собственным функциям консольной балки без нагрузки и ограничений в виде упругого закрепления, то есть один из концов балки закреплен жестко, а другой свободен.

Модель

Рассмотрим консольную балку (рис.1) с массой и упруго закрепленным концом. Левый конец стержня жестко закреплен, а правый – упруго. Перемещения точек балки описываются функцией u ( x , t ) .

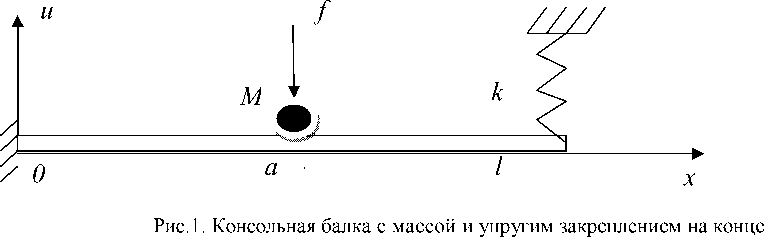
В точке a действует вынуждающая сила f ( t ) = m 0 eto ² sin( tot + ф ) , где m 0 - масса несбалансированного тела, вращающегося относительно некоторой оси, а e -эксцентриситет этой массы, то есть расстояние от центра масс тела до оси вращения. Балка имеет объемную плотность ρ , площадь поперечного сечения F , модуль упругости первого рода E , момент инерции J поперечного сечения относительно нейтральной оси, перпендикулярной плоскости колебаний балки, масса на конце балки M, коэффициент жесткости пружины на конце k .

Можно показать, что дифференциальное уравнение в частных производных, описывающее движение рассматриваемой механической системы, имеет вид:

(pF + MS (x - a)) ^4 (x, t) + EJ ^U (x, t) = v ’ дt2              дx4

= f ( t)S ( x - a )

На и ( x , t ) наложены краевые условия: u ( 0, t ) = 0, | x ( 0, t ) = 0

1 2 ^й ( l , t ) = 0, EJ l u ( l , t ) = ku ( x , t ) д x ²              д x

Положим: и ( x , t ) = V ( x )sin( «t + ф )

.

.

.

д2и        2ТЛ/ х - z _ х д4и д4V . ,, .

Тогда —- = -го V(x)sin(го/ + ф), —- = —-sin(го/ + ф) . д t2                            дx4дx

Подставив в (1), получим:

х хд

( pF + MS ( x - a ) )( - го² V ( x )) + EJ "7j”T( x ) = m 0 еГОЗ ( x - a )

или д 4V      ._

- го¹ pFV ( x ) + EJ ”^t( x ) = го¹MV ( x ) S ( x — a ) + m 0 e^S ( x - a )

Разделим обе части последнего уравнения на ρF и, обозначив

EJM b = —, P = —, mb = PFl , ρFρFl получим д4Vme

- гo²V ( x ) + b —4- ( x ) = го² plV ( x ) S ( x - a ) +—— WS( x - a ) .

дxm

Запишем (3) в безразмерном виде. Для этого в качестве нормировки для амплитуды V ( x )

me примем длину —— , а для координаты x и дельта-функции Дирака S (x - a) примем длину l. mb

T       A moepEA Г д4V ~ moeV (x)U - ~

Тогда V(x) = —— V(x), x = lx, —4~(x) = —0--4—, S(x - a) = - S(x - a), mb                дx        mb    ll где V(x), x, S(x - a) - безразмерные амплитуда, координата и дельта-функция Дирака соответст-

2 ω2m 3 ω2ρF 4 ω2l4

венно. Введем безразмерную частоту в по формуле в =---- 1 =----- 1 = ----, b = —— .

EJ EJ b β ²

Подставив в (3), получим: 2 4

2 m 0 e Р(~А , ^{го l} m 0 e^{V (} x ) _

• -го ---V (x) + —2-4 =

• mb        β  mbl

• 2 me    1         me

= гор!----V ( x )- S ( x - a ) +-- 1го -S ( x - a ) .

• mb      l           mbl

2 me

Сократив на ω ⁰ , получим уравнение движения в безразмерном виде:

m

b

• 1 я 4 ы/7л

~ ~    1 О V x ~ ~ ~ ~ ~   ~ ~ ~

- V ( x ) +—— = ц¥ ( x ) Ж ( x - a ) + 3(x - a )                                           (4)

• в ² - x ⁴

В силу краевых условий (2) также в безразмерном виде справедливо /

V ( 0 ) = 0, V ( 0 ) = 0,

/////

V (1) = 0, EJV (1) = kV(1)

• ω2m

где E = —— E , J = l J

.

Для удобства перепишем дифференциальное уравнение (4) и краевые условия (5) в виде ⁴

—V(x) +   "ТГ2 = ^(xЖx - a) + Ж(x - a)

• в-

• V (0) = 0, V/ (0) = 0,

• V" (1) = 0, EJV/// (1) = kV(1)

где будем считать все величины безразмерными.

Можно доказать, что обобщенное решение дифференциального уравнения (6) имеет вид

V ( x ) = ^G ( x - a)V ( a ) + G ( x - a ) ,

где функция G ( x ) является решением краевой задачи

• .    1 - ⁴ G ( x )        .

• ^{- G} ( x ) ⁺ в 2 ^ x ^= ^{Ж (} x )■

G ( - a ) = 0, G '( - a ) = 0,

G " (1 - a ) = 0, EJG ’’’(1 - a ) = kG (1 - a ) .

Краевая задача (9) решается путем представления G ( x ) в виде суммы обобщенного решения G 0 ( x ) однородного уравнения

A ¹ -⁴ G z , a

• - G ( x ) +——_T ( x ) = 0

в ² - x ⁴

и фундаментального решения G , ( x ) неоднородного уравнения:

• - G ( x ) + в аг ( x ) = Ж ( x ) ,

то есть

G (x ) = Go (x) + G,( x), где

G ₀ ( x ) = c S j ( qx ) + c 2 S ₂ ( qx ) + c 3 S 3 ( qx ) + c ₄ S ₄ ( qx ) .

S 1 ( qx ) =

S з ( qx ) =

cosh ( qx ) + cos ( qx )     , _x

—^2 , S 2 ( qx ) = cosh ( qx ) - cos ( qx )     , _x

-----—-------—-, S 4 ( qx ) =

sinh ( qx ) + sin ( qx )

2^, sinh ( qx ) - sin ( qx )

- функции Крылова, c1, c2, c3, c4 - неизвестные постоянные. Частное решение G* (x) можно представить в следующем виде:

G* (x) = 0( x) qS4( qx), где 9 (x) - функция Хэвисайда, q = в •

Следует заметить, что величины G ( x - a ), V ( a ) зависят от безразмерной частоты в •

Поэтому безразмерная амплитуда V ( x ) в выражении (8) также зависит от безразмерной частоты β .

Заключение

Таким образом, в работе описана математическая модель вынужденных колебаний консольной балки с массой и упруго закрепленным концом. Для анализа полученного дифференциального уравнения с участием дельта-функции был применена техника обобщенных функций, подразумевающая решение этого уравнения в обобщенном смысле. Обобщенное решение полученного дифференциального уравнения опирается на обобщенное решение соответствующей краевой задачи. Выписано выражение для амплитуд точек балки, зависящее от частоты приложенной вынуждающей силы.