Выпучивание прямоугольных пластин при нелинейной ползучести

Введение. Задача анализа устойчивости пластин и оболочек в условиях ползучести актуальна для элементов конструкций из материалов, обладающих свойством старения, находящихся под действием длительных нагрузок, поскольку потеря устойчивости может происходить резко и задолго до исчерпания прочностного ресурса материала. Вопросы совместного учета геометрической нелинейности и ползучести в задачах выпучивания пластин в настоящее время остаются слабо изученными, существующие программные комплексы не позволяют выполнить такой расчёт. Целью настоящей работы выступает разработка алгоритма расчета на устойчивость прямоугольных пластинок с начальной погибью, испытывающих действие нагрузок в срединной плоскости с учетом геометрической нелинейности и ползучести.

Материалы и методы . При получении разрешающих уравнений в основу положены геометрические и статические уравнения теории гибких упругих пластин. Физические уравнения выводятся из предположения, что полные деформации равны сумме упругих деформаций и деформаций ползучести. Окончательно задача была сведена к системе из двух дифференциальных уравнений, в которых в качестве искомых функций выступают функция напряжений и прогиба. Решение полученной системы уравнений выполнялось численно с помощью метода конечных разностей в сочетании с методом последовательных приближений и методом Эйлера. В качестве граничных условий для функции напряжений используется рамная аналогия, как в случае плоской задачи теории упругости.

Результаты исследования . В рамках поставленной цели разработан алгоритм расчета и представлено решение задачи для пластины, сжимаемой в одном направлении равномерно распределенной нагрузкой. Исследован характер роста перемещений при различной величине нагрузки и начальной погиби. Установлено, что при достижении вертикальными перемещениями величин, соизмеримых с толщиной пластинки, скорость их роста начинает затухать даже при нагрузке больше длительной критической.

Обсуждение и заключение . Результаты анализа устойчивости с использованием разработанного алгоритма показывают, что рост прогиба пластины при рассмотренных граничных условиях ограничен, потеря устойчивости не наблюдается при любых значениях нагрузки, не превосходящих мгновенную критическую. Это говорит о возможности длительной безопасной эксплуатации таких конструкций при нагрузке менее мгновенной критической.

Механика

Original article

Buckling of Rectangular Plates under Nonlinear Creep

Serdar B. Yazyev , Anton S. Chepurnenko В

Don State Technical University, Rostov-on-Don, Russian Federation

Introduction. The task of analyzing the stability of plates and shells under creep conditions is critical for structural elements made of materials with the property of aging, which are under the action of long-term loads, since the loss of stability can occur abruptly and long before the exhaustion of the strength resource of the material. Currently, the issues of joint consideration of geometric nonlinearity and creep in the problems of buckling plates remain poorly studied, existing software systems do not provide such calculations. The objective of this work is to develop an algorithm for calculating the stability of rectangular plates with initial deflection, which are subjected to loads in the middle plane, taking into account geometric nonlinearity and creep.

Materials and Methods. When obtaining the resolving equations, the geometric and static equations of the theory of flexible elastic plates were taken as the basis. Physical equations were derived from the assumption that total strains were equal to the sum of elastic strains and creep deformations. Finally, the problem was reduced to a system of two differential equations, in which the desired functions were the stress and deflection functions. The resulting system of equations was solved numerically using the finite-difference method in combination with the method of successive approximations and the Euler method. As the boundary conditions for the stress function, the frame analogy was used, as in the case of a plane problem of elasticity theory.

Results. The solution to the problem for a plate compressed in one direction by a uniformly distributed load has been presented. The nature of the growth of displacements at different load rates and initial deflection was studied. It has been established that when the vertical displacements reach values comparable to the thickness of the plate, their growth rate begins to decay even at a load greater than the long-term critical one.

Discussion and Conclusion. The results of stability analysis using the developed algorithm show that the growth of plate deflection under the considered boundary conditions is limited, stability loss is not observed at any load values not exceeding the instantaneous critical one. This indicates the possibility of long-term safe operation of such structures with a load less than instant critical one.

Введение. Анализу устойчивости тонкостенных конструкций в виде пластин и оболочек уделяется большое внимание, поскольку такие конструкции широко используются в строительстве и других областях техники [1–3]. Одной из актуальных задач в области расчета пластин и оболочек является анализ их напряженно-деформированного состояния в условиях ползучести, что подтверждается значительным числом работ, опубликованных в последнее время по данной проблеме в отечественных и зарубежных источниках. Так, в работах [4–8] исследуются вопросы выпучивания при ползучести композитных тонкостенных конструкций. В статье [9] рассматривается задача устойчивости функционально-градиентных пластин с учетом зависимости свойств материала от температуры. В работе [10] в задаче выпучивания композитных пластин применены методы стохастического анализа. В статьях [11–17] изложены вопросы устойчивости вязкоупругих пластин и оболочек при воздействии динамической и следящей нагрузки, а в статье [18] рассматриваются пластины средней толщины с учетом зависимости свойств материала от времени. Возникающие при решении указанных задач математические трудности приводят к тому, что многие исследователи ограничиваются линейными законами вязкоупругого деформирования или рассматривают случай установившейся ползучести. Большие возможности в задачах расчета пластин и оболочек с учетом ползучести открывает метод конечных элементов. Однако в современные расчетные комплексы, такие как ANSYS, Abaqus, ЛИРА и др., заложен ограниченный набор реологических моделей, применимых для конкретных материалов в фиксированном диапазоне напряжений и температур. Существует необходимость в альтернативных методах расчета, подходящих для произвольных законов вязкоупругого деформирования, в том числе нелинейных.

Целью настоящей работы явилось построение системы разрешающих уравнений для задачи выпучивания пластин прямоугольной формы с нелинейными вязкоупругими свойствами при действии усилий в срединной плоскости, с учетом больших перемещений, а также алгоритма ее решения. Отметим, что проблема устойчивости элементов конструкций с учетом ползучести не может быть решена, как проблема чистой устойчивости. Ее решение требует наличия возмущений в виде начальных неправильностей. Обычно начальные несовершенства задаются в виде начальной погиби или эксцентриситетов приложения нагрузок.

Материалы и методы. Методику расчета рассмотрим на примере пластинки с начальной погибью w ₀( х,у), имеющей шарнирное опирание по контуру и сжимаемой в направлении оси х распределенной нагрузкой p [кН/м] (рис. 1).

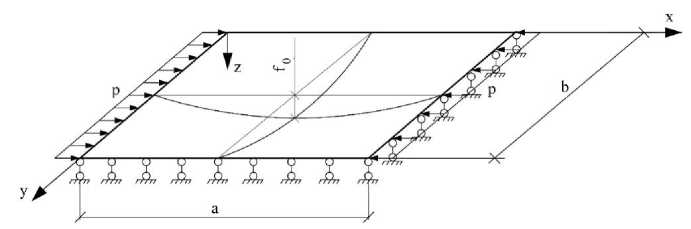
Рис. 1. Расчетная схема

В рассматриваемом случае при наличии ползучести, если сравнивать с теорией упругих гибких пластин, отличие будет проявляться только в форме физических уравнений. Полные деформации могут быть представлены в виде суммы деформаций срединной плоскости (переходящей в поверхность) и изгибных деформаций, которые вызваны изменением показателей кривизны срединной поверхности:

£

x

д ² w          д ² w            д ² w

= £0 - z----;£ = £0 - z----; у = у0 - 2z-----, х    дх2   у у    ду2   ху           дх ду

где £x и e — полные линейные деформации; у^ — полные угловые деформации; £0 и £0 — линейные деформации срединной поверхности; у0 — угловые деформации срединной поверхности.

Для деформаций срединной поверхности может быть записано уравнение неразрывности деформаций [19]:

д ² £ 0    д ² £ у   д ² у ⁰ _(д ² ( w + w ₀ )Y д ² ( w + w ₀ ) д ² ( w + w ₀ )    (д ² w ₀Y   д ² w ₀ д ² w₀

д у    д^у  д х д у ~(   д Х д У  J      д Х ²        д у ²       1а Х д У ^J   д х ²   д у

Для материалов с вязкоупругими свойствами полные деформации можно представить в виде: ^{1                          1}                            2 ^{( 1} + ^v)

£ х = ^(° х -VO у ) + £х ;£ у = ^(° у -VO х )+£у ; Уху =^---Т ху +Уху , где £*,£*,у*, — деформации ползучести; E — модуль упругости; v — коэффициент Пуассона; ах, ау, тху — величины компонентов напряжений по соответствующим направлениям.

Выразив в (3) компоненты напряжений через деформации, запишем физические соотношения в обратной форме:

О = E     +V£v -(£* +v£* У); СТХ = E  (б +VEX -(б* +V£* Y); т  = —E—- (у  -у* ).(4)

^х 1 ^2 ^{х у х у х} 1 ^ 2 ^{у х у х ху}    2 (1 + V У

Связь внутренних силовых факторов с напряжениями определяется интегральными соотношениями: h/2                    h/2                 h/2                     h/2                      h/2

Nx = J o,dz; N = f ovdz; S = f т„dz; M = f ozdz; M = f ozdz; H = f т zdz,(5)

x           x        y           y                 xy         x           x          y           yxy

- h/2                - h/2              - h/2                  - h/2                   - h/2

где N и N — погонные продольные силы; S — погонные сдвигающие силы; M и M — погонные изгибающие моменты; H — погонные крутящие моменты; h — толщина пластинки.

Далее подставим (1) в (4), а также (4) в (5). В итоге получим:

N = Eh-(£0 +V£0)-N*;Ny = Eh"(£0 +V£0)-N*; S =  .Eh . у0 -S х 1 -V2 x х у/ х у 1 -v2V у х’ у      2(1 + v)

M x

( д ² w    д ² w

- D I --- + v---

( д х ²      д у ²

- м х ; М у

( д ² w    д ² w |                     д ² w

- D I--- + v---I- М * ; H = - D ( 1 -v )-- H * ,

( д у ²      д х ² J                     ^} д х д у

Механика

где D =

Eh ³

12 ( 1 -v ² )

— цилиндрическая жесткость пластинки, N * =

E

1 — v ²

h /2

1 ( s : +^vs ; ) dz,

- h /2

h /2                                                 h /2

N* =----- J (s* +vs*) dz, 5* = —----- J y* dz, y 1 — v2 -h/2V y      x)           2(1 + v)-h/2 xy

E    h /2                           E    h /2                            E     h /2

M * =----- J (s * +vs* ) zdz , M * =----- j  s * + vs* ) zdz , H * =—----- J y* zdz .

^x 1 — v ² - h /2^{V x}      y’         y 1 — v ² - h /2^{V y      x}’              2 ( 1 + v ) - h /2 ^xy

Величины N*, N*, 5*, M*, M*, H* имеют размерность внутренних усилий и определяют вклад деформаций ползучести в перераспределение усилий.

Статические уравнения теории гибких пластин имеют вид [19]:

д N д 5   _ д 5 д N

—- + — = 0; — + —- = 0; д x   д у    д x   д у

д²М д²Н  д ² M      д² ( w + w„)      д² ( w + w„)      д² ( w + w„)

-— x + 2— +---^- + N _(    02 + N _(    0 ) + 2 5 _(    °2 ₊ q = o.

д x ²      д x д у   д у ²            д x ²              д у ²             д x д у

Здесь q — нормальная нагрузка по поверхности пластины, которая в данной задаче равна нулю.

Удовлетворить первым двум статическим уравнениям можно при помощи функции напряжений Эри, введенной по формулам:

д ²Ф „ д ²Ф „ д ²Ф —; N = —; 5 =-- .

д у ²         д x ²        д x д у

После подстановки последних трех равенств из (6) в последнее статическое уравнение в (7) и с учетом (8), получим первое разрешающее уравнение:

где q ^*

—

D V 4 w = q + q * +

д ² Ф д ² ( w + w ₀) д ² Ф д ² ( w + w ₀)

д x ²      д у ²

д у ²      д x ²

—

^ д ² Ф д ² ( w + w ₀) д x д у   д x д у

д ² M *   „ д ² H *   д ² M *

----- + 2     +----- д x ²      д x д у     д у ²

Чтобы получить второе разрешающее уравнение, необходимо выразить из (6) деформации поверхности:

срединной

^s 0

N — v N + N * — x  yx

Eh

v N * _ 1 Г д ² Ф

-

^s у

N — v N + N * — v N * yxyx

Eh

Eh ( д у ²

v--- + N * — v N * ;

д x ^{2       x       у} J

1 Г д ² Ф

Eh I д x ²

—

д2Ф v---+ N* —vN*

ду 2     уx

2 ( 1 + v)z

Y⁰ =-^---- Ч 5 + 5 * ) =

Eh

2 ( 1 + v ) 2 д 2 Ф ---

Eh

д x д у

*.

Подставив (10) в (2), получим:

— V 4 Ф =

Eh

д ² ( w + w ₀ ) | Г д ² w ₀ )

—

—

д x д у

д x д у J

Г д ² N +vl —— ^x

д ² ( w + w ₀ ) д ² ( w + w ₀ )   д ² w ₀ д ² w₀

д x ²          д у ²

д ² N * ) д 2 N * д ² N у

д x ²   д у ²

1             д ² 5 *

+ — (2 ( 1 + v)----+

Eh       ⁷ д x д у

—

—

д x ²      д у²

д у ²      д x²²

).

Таким образом, для рассматриваемой задачи получена система разрешающих уравнений из двух

дифференциальных уравнений четвертого порядка (9) и (11). Уравнения (9) и (11) являются нелинейными. В полученных уравнениях величины Ф и w представляют собой функции координат x , y , а также времени t . В явном виде в данных уравнениях время отсутствует, зависимость от времени закладывается в деформации ползучести s * , s * , у *, , которые учитываются введением интегральных величин N * , N * , 5 * , M * , M * , H • .

Для изображенной на рис. 1 расчетной схемы граничные условия записываются в виде:

при x = 0, x = a : N =

при у = 0, у = b : N =

д ² Ф

д у ² д ² Ф

д x ²

= — p ; 5 =--= 0; w = 0; M_r = 0;

д x д у

= 0; 5 =--= 0; w = 0; M„ = 0.

д x д

Уравнение (11) при малых перемещениях, в случае пластины из упругого материала, представляет бигармоническое уравнение, которое используется для решения плоской задачи теории упругости в напряжениях. Граничными условиями по функции напряжений для бигармонического уравнения может служить рамная аналогия. Контур пластины рассматривается как рама и функция напряжений на контуре будет равна в ней изгибающему моменту M , а ее производная по нормали к контуру — продольной силе N . Эпюры M и N в раме могут быть построены в одной из основных систем метода сил (ОСМС). Основная система, а также эпюры изгибающего момента и продольной силы в раме показаны на рис. 2.

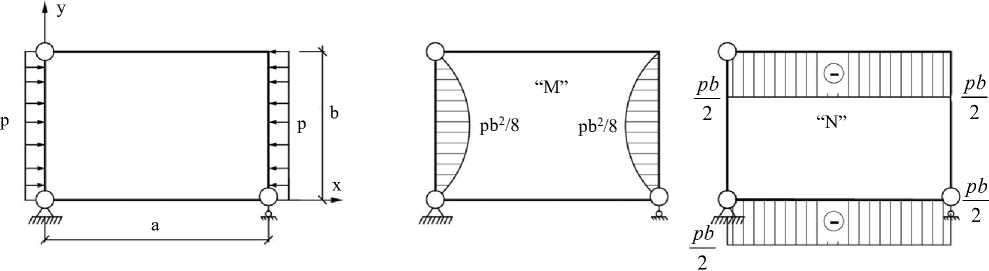
Рис. 2. ОСМС и эпюры изгибающих моментов и продольных сил

Если вертикальные перемещения не превышают четверть толщины пластинки, то можно принять усилия в срединной поверхности не зависящими от координат x и y (Nx = -p, Ny = S = 0 ) и использовать для расчетов линеаризованное уравнение:

д ² w

d V4 w+p   = q дx2

—

д ² Ч _p       0 _.

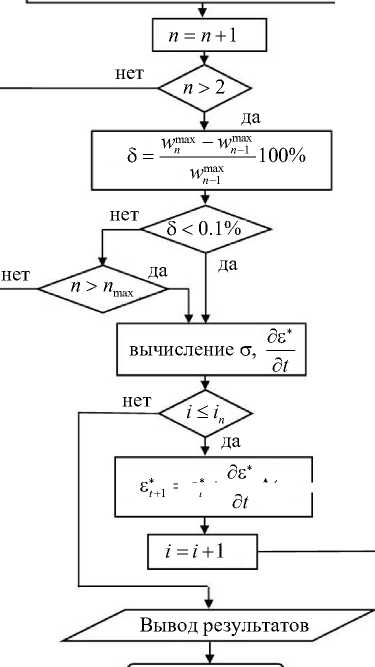
Аналитическое решение системы уравнений (9) и (11) связано с большими трудностями. Авторы предлагают решать данную систему численно. Используется метод конечных разностей (МКР) в комбинации с методом последовательных приближений. Для определения деформации ползучести во временной области применяется метод Эйлера. В качестве первого этапа выполняется решение для упругой пластинки. Нагрузка p прикладывается ступенчато с небольшим шагом. При начальных значениях нагрузки прогибы w1 вычисляются путем решения упрощенного уравнения (13). Затем выполняется подстановка вычисленных значений w1 в дифференциальное уравнение (11). Это позволяет определить функцию напряжений. Следующим шагом является решение дифференциального уравнения (9) с использованием известных величин функции Ф, что позволяет определить узловые величины прогибов w‘. После этого выполняется подстановка значений w2 = (w + w')/2 в уравнение (11). Повторение итерационного процесса на каждом шаге происходит до тех пор, пока относительное расхождение с нормами векторов узловых значений прогибов w и w' больше заданного значения (авторами оно принималось равным 0,1 %). Для второго шага по нагрузке начальным значением w в каждом узле выступает конечный результат, полученный на первом шаге. Методика расчета во временной области с учетом ползучести аналогична. Интервал времени, на котором исследуется процесс, делится на шаги ∆t. В случае задания закона вязкоупругого деформирования в дифференциальной форме величины деформаций ползучести на шаге t + ∆t вычисляются на основе известной скорости их роста в момент времени t с использованием аппроксимации по Эйлеру:

де* .

е * +а . =е* + — A t .                                              (14)

д t

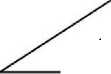
Блок-схема алгоритма расчета на ползучесть приведена на рис. 3.

Отметим, что система уравнений (9) и (11) позволяет использовать схемы более высокого порядка точности, например, метод Рунге-Кутта четвертого порядка. При этом для достижения той же точности результатов можно задавать заметно большие шаги по времени. Однако при увеличении шага есть вероятность не уловить эффекты неустановившейся ползучести в начальные моменты времени. А при одинаковом шаге по времени метод Рунге-Кутта, по сравнению с методом Эйлера, требует выполнить в четыре раза больше операций.

Механика

Начало

Решение упругой задачи:

i = 1; t = 0; е ^; = е * = у* = 0; Ф = Ф x     y     xy

n = 1  *----------

_______    ♦   __________

Определение w из ур-я (9)

нет

w m = ( w n ⁺ w n - i )/2

* ------

Подстановка w_n в (11) и определение Ф_л

= е; + — A t

Конец

Рис. 3. Блок-схема алгоритма расчета на ползучесть

Результаты исследования . Рассмотрена полимерная пластинка из поливинилхлорида размерами a = 2 м, b = 2 м, h = 1 см при E = 1480 МПа, ν = 0,3. В качестве закона, определяющего скорость роста деформаций ползучести, было принято нелинейное уравнение Максвелла-Гуревича:

де * д t

* f _ij

—, i = x , y , j = x , y;

П *

**

i j              j       0 ij         » j ^;

( f f *

n* =n0 expl -fm^1 I;/:x = 3(arr -^0)-E„£' I ml          2

где 8,у — символ Кронекера; ст0 = Jx / 3, J = ах + ау — первый инвариант тензора напряжений; n*, E® и m — реологические параметры материала, называемые начальной релаксационной вязкостью, модулем высокоэластичности и модулем скорости.

Индексами rr в формуле (15) обозначено направление главных напряжений.

Для ПВХ значения реологических параметров авторами были взяты из работы [20]: E ∞ = 5,99∙10³ МПа, m *=12,6 МПа, n * = 5,44^10 7 МПа^с. Форма начальной погиби w ₀( x,y ) принималась в соответствии с первой формой потери устойчивости пластинки из упругого материала:

w ₀

п x . пу

( X , у ) = f ) Sin — sin . ab

Для пластины из упругого материала без начальных несовершенств критическая нагрузка, в случае целого отношения сторон a/b, определяется по формуле [19]:

4 п ² D

^Ркр =   b ^

.

Для верификации разработанного алгоритма расчета первым этапом было выполнено решение тестовой упругой задачи и сравнение результатов с расчетом в конечно-элементном пакете ЛИРА-САПР (рис. 4). Величина стрелы начальной погиби f 0 задавалась равной 0,15 мм. Размер сетки при использовании МКР составлял 20×20, количество шагов по нагрузке — 200. При расчете в ПК ЛИРА-САПР выполнялось разбиение пластинки треугольными конечными элементами с шагом триангуляции 0,1 м. Величина шага по нагрузке принималась такая же, как и при использовании МКР. Значение критической нагрузки для упругой пластинки, вычисленное по формуле (17), составило 1340 Н/м. В таблице 1 показано сравнение вертикальных перемещений в центре пластинки для различных значений нагрузки, полученных по авторской методике и при помощи метода конечных элементов (МКЭ). Прогибы, вычисленные с использованием двух альтернативных методов, достаточно близки, за исключением нагрузки 1330 Н/м. Отклонение при этой величине нагрузки можно объяснить тем, что при приближении к критической нагрузке перемещения устремляются в бесконечность.

z

'-1 х

1,37

1,82

3,19     3,65

2,28      2,73

0     0,0365    0,0456    0,911

Нелинейное загружение 1 Изополя перемещений по Z(G) Единицы измерения - мм

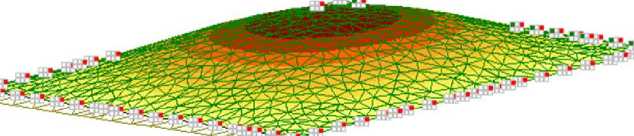
Рис. 4. Изополя вертикальных перемещений в ПК ЛИРА-САПР ( p = 1330 Н/м): нелинейное загружение 1, изополя перемещений по Z(G), еденицы измерения — мм

Таблица 1

Сравнение результатов расчета по авторской методике и при помощи МКЭ

p , Н/м	w∙ 103, мм
	ЛИРА-САПР	Aвторская методика
133	16	16
266	37	37
399	63	63
532	98	99
665	146	148
798	218	221
931	336	342
1064	562	578
1197	1163	1229
1330	3646	4229

Механика

В статье [21] показана возможность перехода от решения упругой задачи расчета пластин к решению в конце процесса ползучести. Величину длительной критической нагрузки p ∞ можно получить, заменив цилиндрическую жесткость D упругой пластинки на длительную цилиндрическую жесткость D ∞ , которая определяется по формуле:

D

и

a h ³

12 ( a ² -Р ² ) ,

„    1  ,   1 п V ,1

где a =   +    ; в =   +

E E    E2

и

и

Для вязкоупругих стержней и круглых пластин было ранее установлено, что в случае p <  p ∞ , рост перемещений во времени замедляется, и стрела прогиба приходит к конечному значению. Если p = p ∞ , прогибы растут с постоянной скоростью. При p >  p ∞ скорость роста прогибов возрастает.

Авторами также проведен анализ характера роста прогибов во времени для p <  p ∞ , p = p ∞ и p >  p ∞ для различных значений максимальной начальной погиби f 0 . Кривые изменения прогиба с течением времени в центре пластины при p = 0,9 p ∞ , p = p ∞ и p = 1,1 p ∞ приведены соответственно на рис. 5–7.

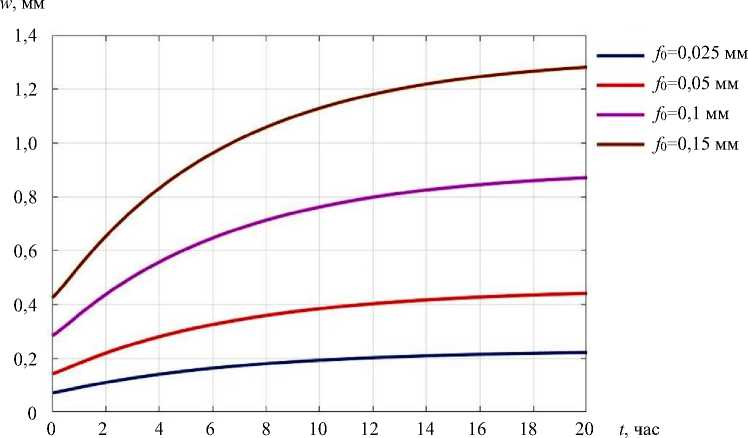
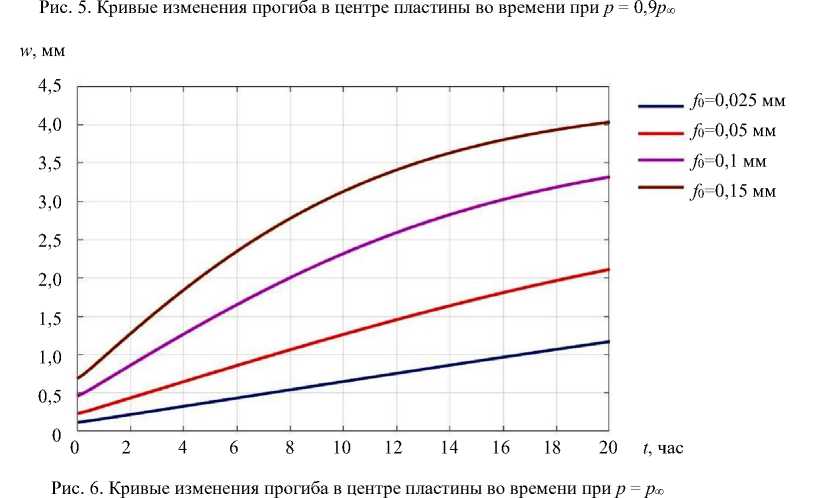
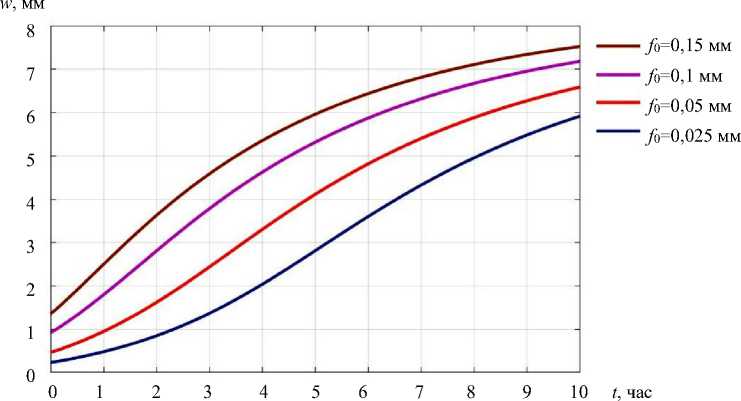
Рис. 7. Кривые изменения прогиба в центре пластины во времени при p = 1,1 p ∞

Обсуждение и заключение. Из рис. 5 видно, что при p <  p ∞ стрела прогиба всегда приходит к конечному значению, независимо от значений начальных несовершенств. В то же время при p ≥ p ∞ полученный в [21] характер роста прогибов имеет место только при малых перемещениях. При достижении прогибами значений, превышающих примерно четверть толщины пластины, скорость роста деформаций начинает убывать даже в случае нагрузок, превышающих длительную критическую. Следует также отметить полное отсутствие участка с возрастающей скоростью роста перемещений для пластин с большими начальными искривлениями. Объяснить выявленные эффекты можно перераспределением усилий N , N _у , S в срединной поверхности.

Резюмируя вышесказанное, можно сделать вывод, что вертикальные перемещения пластины, шарнирно опертой по контуру, при действии сжимающей нагрузки по одной оси, всегда приходят к конечному значению, если нагрузка не превышает мгновенную критическую. Иначе говоря, при рассмотренном закреплении и нагружении пластина в условиях ползучести находится в устойчивом равновесии.

Полученные уравнения и алгоритм вычислений позволяют рассчитывать пластинки из произвольных вязкоупругих материалов при любых вариантах закрепления. Закон связи между напряжениями и деформациями ползучести также может быть задан произвольно.