Выравнивание интенсивности фокального пятна сфокусированного гауссового пучка

Выравнивание плотности энергии в сечении когерентных световых пучков является важной задачей для технологических и информационных применений лазеров. Для этой цели используются дифракционные оптические элементы (ДОЭ), преобразующие волновой фронт таким образом, чтобы в заданной плоскости сформировалось требуемое распределение интенсивности.

История этого вопроса такова. В работе [1] было предложено использовать бинарную дифракционную решетку для перераспределения энергии в пучке с целью ее выравнивания. Использование геометро-оптического приближения для расчета ДОЭ, выравнивающего поперечное распределение интенсивности коллимированного гауссового пучка предложено в [2]. В [3] с помощью киноформной линзы экспериментально осуществлено выравнивание интенсивности гауссового пучка в дальней зоне дифракции. Итеративный подход для расчета фазового ДОЭ, преобразующего гауссовое распределение интенсивности пучка в супергауссово распределение интенсивности в фокусе линзы, предложен в [4]. При этом численно было показано, чго предложенный алгоритм эффективно работает, если размер области фокусировки больше нескольких (4-5) минимальных дифракционных пятен.

Геометро-оптическому расчету голографического фильтра для выравнивания профиля интенсивности пучка света посвящена работа [5]. Недостаток голографических фильтров в том, что они обладают низкой энергетической эффективностью. В [6| голографический фильтр для выравнивания поперечной интенсивности пучка рассчитывался итеративным методом в приближении скалярной дифракции. Это позволило достичь более высокой точности формирования требуемого распределения интенсивности. Численный эксперимент с фоку сатором, преобразующим гауссовый пучок в квадрат с постоянной интенсивностью проводился в [7]. Было, в частности. показано, что геометро-оптический метод дтя расчета ДОЭ применим, если размер области фокусировки больше семи дифракционных пятен.

В [8] с помощью двух голографических фильтров, осуществлено экспериментально преобразова ние эллиптического гауссового пучка в ближней зоне дифракции в квадрат с постоянной интенсивностью и фазой.

В этой же работе, и независимо в работе [9], получены аналитические формулы для фазы ДОЭ, фокусирующего гауссовый пучок в малый квадрат с постоянной интенсивностью. В [10] приведен сравнительный численный эксперимент по расчету ДОЭ двумя способами: геометро-оптическим и итеративным в приближении Френеля. Показано, что наилучшего результата по выравниванию гауссового пучка можно достичь, применяя геометро-оптическое решение [8,9] как начальное приближение дтя итеративного процесса.

Выравнивание профиля интенсивности пучка полупроводникового лазера с помощью бинарной фазовой дифракционной оптики продемонстрировано в [11].

В [12] также с помощью бинарного отражающего ДОЭ с наклонным падением экспериментально показано выравнивание пучка гелий-неонового лазера в плоскости дефокусировки. Экспериментальные исследования по фокусировке гауссового пучка СО2 лазера в прямоугольник с равномерной интенсивностью с помощью бинарного и многоградационного ДОЭ проведены соответственно в [13] и [14].

Во всех перечисленных работах, за исключением [3], размер сфокусированного с помощью ДОЭ прямоугольного или круглого равномерного распределения интенсивности составлял несколько минимальных дифракционных пятен. То есть полной фокусировки гауссового пучка не происходило. В [15] кратко замечено, что выравнивать гауссовый пучок в фокальной плоскости в области минимального дифракционного пятна можно с помощью бинарной фазовой пластинки с цилиндрической ступенькой.

В данной работе рассматривается вопрос о возможности выравнивания интенсивности гауссового пучка в плоскости фокусировки (с минимальным увеличением размера дифракционного пятна) с помощью простого фазового оптического элемента. Введен новый критерий, согласно которому степень выравнивания интенсивности светового пучка рассматривается не как степень близости к функции с постоянной интенсивностью в некоторой области плоскости фокусировки, а как степень достижения максимальной энергии в области, в которой интенсивность пучка спадает до заданного уровня (например, до уровня 60% от максимального значения). Дело в том, что в некоторых устройствах лазерного бесконтактного контроля качества гладких поверхностей (например, кремниевых пластин) зарегистрированное отраженное излучение анализируется после пороговой фильтрации. А порог устанавливается по некоторому уровню спада интенсивности.

В данной работе на численных примерах показана эффективность использования для выравнивания интенсивности гауссового пучка в пределах минимального дифракционного пятна простого бинарного ДОЭ в виде цилиндрической (или прямоугольной) ступеньки, высота и радиус которой зависят от радиуса перетяжки пучка и от расстояния до нее. На модельном примере с заменой фазового ДОЭ со скачкообразной фазой на непрерывный амплитудный пространственный фильтр показано, что удается достичь увеличения с 40% до 65% доли энергии, попадающей в кружок, в котором интенсивность спадает на 40%. При этом радиус такого кружка увеличивается вдвое.

/. Общая постановка задачи

В ряде устройств лазерной диагностики поверхностей наличие дефектов на поверхности обнаруживается по анализу отраженного лазерного пучка, который предварительно был сфокусирован на поверхность. Равномерность отклика системы на дефект, попавший в разные участки светового пятна на поверхности зависит от равномерности распределения интенсивности в пятне фокусировки.

Кроме того, на этапе электронной обработки зарегистрированного отраженного излучения обычно применяется пороговая фильтрация шумов, в результате которой в канат обработки проходит сигнал, значение которого больше заданного уровня (например, больше 60% от максимального значения интенсивности).

Поэтому актуальной задачей является формирование фокального пятна с таким распределением интенсивности, которое обеспечивает максимальную долю энергии в пятне, ограниченном заданным уровнем интенсивности.

Формально такая задача в одномерном варианте может быть сформулирована так. Требуется найти фазовую функцию <р(х) ДОЭ. которая максимизирует функционал-критерий

M = l/2p(x)[sgn(/(x)-^,) + l]dx, (I)

где 1(х) - распределение интенсивности в Фурье-плоскости линзы, то есть в плоскости фокусировки пучка с амплитудой А_о(^. 0<а<1 - параметр, задающий уровень спада интенсивности по сравнению с максимальным ее значением /_т, sgn(x) - знаковая функция.

Функционал (1) максимизируется при условии сохранения энергии ^ = р(х)бхи сохранения ра диуса исходного пучка W7 = j^/ly^d^.

Интенсивность 1(х) связана с искомой функцией фазы (р(^) преобразованием Фурье

/(x)=H/J^(Oexp[lHO-'fcf//k , (2)

где к=2л/Х - волновое число света с длиной волны А / - фокусное расстояние линзы. На рис. 1 показана оптическая схема использования ДОЭ для выравнивания интенсивности гауссового пучка. На рис. I гауссовыи пучок с длиной волны X и радиусом перетяжки м-р попадает на ДОЭ и линзу Л, расположенные на расстоянии г от перетяжки. Радиус гауссового пятна в плоскости ДОЭ равен w, радиус на котором происходит скачок фазы ДОЭ равен R. Минимальный кружок дифракции с интенсивностью Цг) формируется на расстоянии /, которое не равно фокусному расстоянию линзы / Минимальный диаметр пучка формируется на расстоянии /, которое удовлетворяет уравнению линзы:

В общем случае задачу максимизации критерия М из уравнения (1) можно приближенно решить градиентным итеративным методом [16]:

Ф„л to = фп (х) + h„ fM , (3) 5y„to где ^м - градиент функционала, Ип - шаг ите-

^Дх)

ративного процесса, <р_п(х) и (p_n^i(x) - оценки фазы ДОЭ на п- ом и (л-УДом шагах.

Заметим, что функционал (1) не зависит от конкретного вида функции, которая в качестве эталонной обычно вводится в квадратичный критерий |Ю]:

М, = J[/(x)-/„(x)fA ,                 (4)

где Iq(x) - заданная функция интенсивности фокального пятна, например, I₀(x) = rectfx/a) , где а - ра-

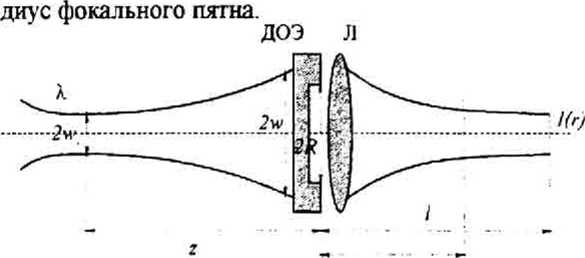
Рис. 1. Оптическая схема для выравнивания интенсивности сфокусированного гауссового пучка

• 2.    Бинарный фазовый ДОЭ

Сформулируем задачу. Требуется выравнить интенсивность в фокальном пятне без существенного увеличения размера самого пятна. При выравнивании интенсивности дифракционного пятна круглой формы неизбежно происходит увеличение его радиуса в 1.5 - 2 раза. Понятно также, что искомый ДОЭ должен расходящийся параболический фронт гауссового пучка разделить на две части (центральную и периферийную), внеся фазовую задержку между ними. При этом ДОЭ не должен изменять кривизну волнового фронта, чтобы не увеличить расходимость гауссового пучка. Выравнивание интенсивности в дифракционном пятне должно происходить не за счет увеличения расходимости пучка, а за счет интерференции разных частей пучка (центральной и периферийной), получивших относительную фазовую задержку. Функция пропускания простейшего ДОЭ, обладающего указанным свойством имеет вид:

[1,     0<г<Л

т(г) = ]                      ,                  (5)

|ехрО#),г > R где О - фазовая задержка, R - радиус цилиндрической фазовой ступеньки ДОЭ, г - радиальная координата. Функция (5) имеет два параметра R и 9, подбором которых достигается эффективное выравнивание интенсивности.

Выражение для комплексной амплитуды света в фокальной плоскости линзы для гауссового пучка, прошедшего ДОЭ (5), имеет вид:

F(p, z) = Л(х)jexp[a(z)r2 ]х r(r)Jо М^Р/ j>dr, (6) о где

A(z) = 2nkf ¹ 1 -н — .

\ 2о 7

a(z) = -w 2(z) + zG"‘(z), w U) = w* l--r1, \ Z0 )

G(z) = H'02z0z"'p4-~-

z0 =*w2/2,

p - радиальная координата в фокальной плоскости линзы. w(z) - радиус гауссового пучка, G(z) - радиус кривизны волнового фронта, J₀(x) - функция Бесселя нулевого порядка, z - расстояние от перетяжки до плоскости ДОЭ (рис. 1), г о - расстояние от перетяжки, на котором фронт гауссового пучка имеет максимальную кривизну.

Выражение (6) можно записать в виде:

F(p,z) = A^e,y -1)(2/а)"'схр(а^2)х х \их (2iaR2, bR) - i L'2 (HaR1, bR)]}-          (11)

-A^IaY¹ exp|

I 4a / где

/ u„(^)=2(-i)‘- J_lh„W;

U_n(x,y) - функции Ломмеля, J_n(y) - функции Бесселя, b^kpY a=a(z). При получении выражения (11) были использованы справочные интегралы [17]:

h

[ ехр(аг²)Л - (2а) ¹ ехр — [, ;           W

R

J exp(ar² )J₀ Vbrydr =

о

= (2га)¹ explaR^VG^aR^bRVi^^^^

Заметим, что при 6=0 в ур. (11) остается только второе слагаемое, описывающее гауссовый пучок.

Для точек в фокальной плоскости, близких к центру, при выполнении условия b< I 2aR I, удобно использовать другие функции Ломелля [17] :

РДХ, У) = COS —+ —+  + 2 2х 2 J

( х Ik Уп

у)

Тогда вместо уравнения (11) получим:

F(p,z^A(.z^l-e'6X2iay'x

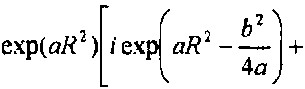
+ V_x (2iaR*, bR) -i^ ^iaR¹, 6/?)]

-(2a)"1 exp[ И

Чтобы оценить оптимальное значение радиуса R цилиндрической ступеньки рельефа ДОЭ по отношению к радиусу пучка w(z) упростим выражение (16). Для этого рассмотрим значение амплитуды в центре Фурье-плоскости при р0 и Ь=0.

Скачок фазы ДОЭ 0 выберем равным л. Пусть также ДОЭ расположен в перетяжке гауссового пучка: z=0, G=0, w^mv Тогда интенсивность в центре 1(0) будет связана с радиусом R выражени ем

ДО) = /₀ [ехр(-4Л²) - 2 ехр(-ЗЯ²) -

+ 2 ехр(-2А2) - ехр(-Я2) + А

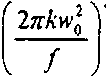
где R_x = R(w_oy\l_o =

В уравнении (17) учтено, что Vух,0)^-0, У_о(х,О)=1. На рис.2 показана зависимость 1(0) от Ri, график которой достигает минимального значения при

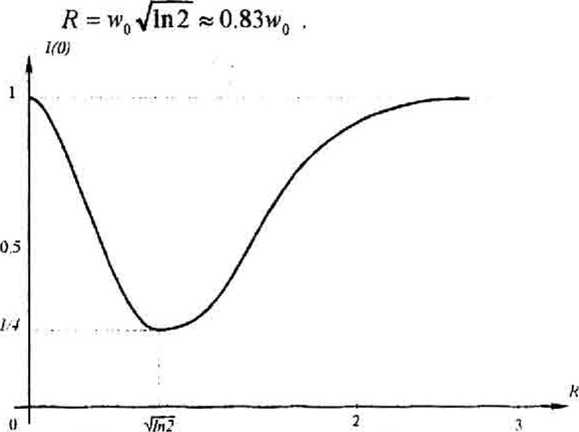
Рис. 2. Зависимость нормированной интенсивности гауссового пучка в центре фокальной плоскости от радиуса скачка фазы ДОЗ

Сложность выражения (16) не позволяет аналитически сделать оценки для оптимального выбора параметров фильтра R, 6. Хотя можно видеть, что при любом радиусе скачка фазы ДОЭ R интенсивность в центре не уменьшается до нуля, и что искомое значение отношения ^и^ должно быть близко к единице.

• 3.    Амплитудный ДОЭ как модель фазового бинарного ДОЭ

Пропускание фазового ДОЭ (5) при 0=л можно записать в виде

Дифракция когерентного света на фазовом ДОЭ (18)во многом будет аналогична дифракции на соответствующем амплитудном ДОЭ с пропусканием r^l"" - (19)

Это предположение позволяет оценить оптимальное значение R. Пусть ДОЭ (19) расположен в перетяжке гауссового пучка (8), тогда сразу за ДОЭ амплитуда светового пучка будет описываться функцией, имеющей вид ‘мексиканской шляпы’

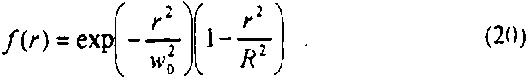
Заметим, что при R = wJ41 функция (20) будет описывать первую моду Гаусса-Лагерра, так как первый многочлен Лагерра имеет вид L4x) = 1 - х

На рис.З показаны нормированные графики функций амплитуды гауссового пучка до оптического элемента (кривая 1) и после оптического элемента (кривая 2). Функция мексиканской шляпы часто используется в задачах цифровой обработки изображении с помощью преобразования волнового пакета [18| и. фактически, является второй производной от гауссовой функции.

‘ J(r)

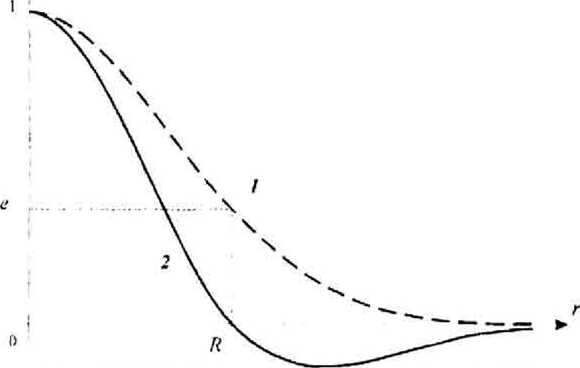
Рис. 3. Графики гауссовой функции (кривая 1) и функции “мексиканская шляпа" (кривая 2)

В плоскости фокусировки сформируется световое поле с комплексной амплитудой

I*\p_xV ^хрк-р^-Т^УрЪ ,      (21)

где

27^,,       р

—"• А = —Г =

/      Ро

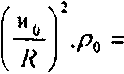
If

^0

р,_ - радиус гауссового пучка в ()юкальной плоское ти. Распределение интенсивности будет иметь вид

/(р) = |/'(/9)|2 =/осхр(-2р1:)[1-7+/А‘р • где /0 = F^ Точки экстремума функции (22) сле дующие:

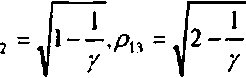
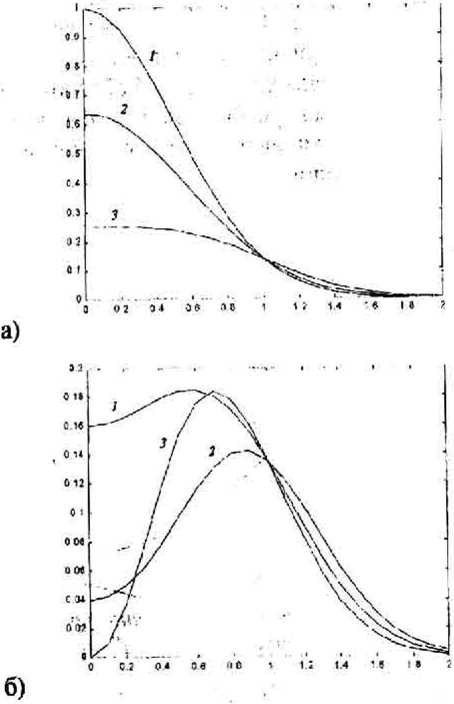
На рис 4 показаны п^афики интенсивности (22) при различных значениях параметра у. у =0 (1а), у~ 0.2 (2а). 7=0.5 (За), у =0.6 (16), у ^ 8 (26). у=1 (36), у- 2 (в). Из рис. 4 видно, что точка pi I является узловой, так как при любом значении параметра у имеет место равенство:

Кр = 1) = /₀ ехр(-2)

Из рис.4 также видно, что при 0 < у < 0.5 функции интенсивности имеют один максимум в центре при р^0 (рис.4а): при 0.5 <у<1 - минимум в центре и максимум на периферии (рис.4б): при у> 1 - два максимума и один минимум с нулевым значением. Заметим также, что случай у = 2 (рис 4в) соответствует первой моде Гаусса-Лагерра (/( = M'₃/V2) и интенсивность на выходе такая же как на входе, а именно "мексиканская шляпа".

Из уравнений (25), (26) следует, что при фокусировке гауссового пучка в фокальном пятне радиуса

Рю = — = «0.51 Ро V V 0.6

(половина радиуса гауссового пучка в фокальной плоскости), на котором значение интенсивности составляет 60% от максимального, сосредоточено 40% энергии всего пучка.

Уравнения, аналогичные уравнениям (25) и (26), но для фокального пятна, сформированного ДОЭ (19) при /=0.5 примут вид (/?;о=1);

^ = ехр(-2А10)(1 + р|20)1 =

= 4ехр(-2)«0.54

£q.5⁼| Jexp(-2x²)(l + x²)²xtZxlx

X jexp(-2x2)a+x2)2xdx| =            (28)

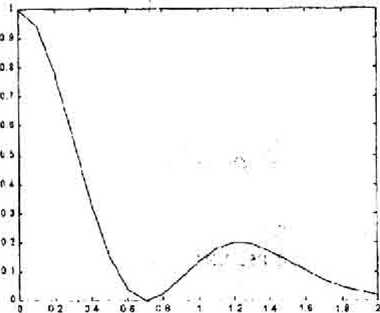
Рис. 4. Графики интенсивности из уравнения (22) при различных значениях параметра у

О (al), 0.2 (а2), 0.5 (аЗ), 0.6 (61), 0.8 (62), 1 (63), 2 (в)

Значение у = 0.5 - предельное значение, при котором еще нет локального минимума в центре фокального пятна. В этом случае радиус ДОЭ удовлетворяет уравнению;

R = w₀^. (24)

Сравним энергетическую эффективность двух фокальных пятен при /=0 (в отсутствии ДОЭ) и при /=0.5 (при оптимальном выборе радиуса ДОЭ). Энергию в фокальной плоскости будем рассчитывать в круге радиуса, на котором интенсивность составляет 60% от максимального значения в центре. Для гауссового пучка будем иметь;

^^■=еф(-2р,!0) = 0.6 ,(25)

[АО                 Г*'\“

J ехр(-2х2 )xdx х Jехр(-2х2 )xdx=

П                 ) \о)

= 1-ехр(-2/э20) = 0.4 .(26)

= l-0.5exp(-2p2)x

x[5 + 6A2 + 2^o]«O.65

Из уравнений (27) и (28) следует, что при фокусировке гауссового пучка с помощью модельного ДОЭ (19) при условии (24) в фокальном пятне в круге радиуса рю= 1 (в два раза большем, чем в отсутствии ДОЭ), на котором значение интенсивности составляет 54% от максимального значения, сосредоточено 65% энергии всего светового пучка.

• 4.    Алгоритм расчета фазы ДОЭ, основанный на решении интегрального уравнения

На рис. 5 показано гауссово распределение интенсивности света (кривая 1)

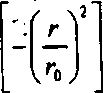
которое в нашем случае имеет следующий параметр r0=w/V2, w=-^-- радиус амплитуды

ЛН-0 гауссового пучка в фокальной плоскости.

Кривая 2 на рис. 5 показывает форму идеально выровненной интенсивности в фокальной плоскости. Значение интенсивности 7 вычисляется из условия сохранения энергии в пятне радиуса w:

ям11 = ^(w)

где

W(w) = 2/г J ехр[- (г / r₀ )]² г d г о

энергия нормированного гауссового пучка в пяти е радиуса w.

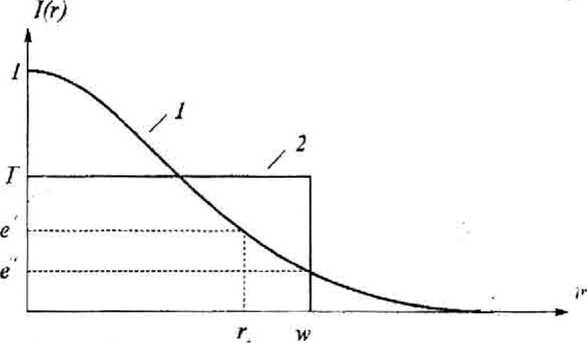
Рис. 5. Интенсивность гауссового пучка на выходе системы (кривая 1) и форма желаемой интенсивности, (кривая 2)

Из (30), (31) получим выражение для средней интенсивности:

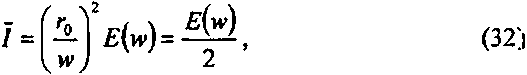
где

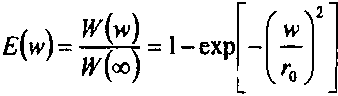
энергетическая эффективность, то есть часть энергии света, попадающей в круг радиуса w. В нашем случае в круге радиуса w=0.028mm эффективность равна s=100%£^,(w)=86%.

Среднеквадратичная ошибка выравнивания интенсивности вычисляется по формуле

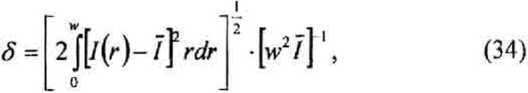
где /(г) - рассчитанная интенсивность, / - заданная интенсивность. Эффективность для рассчитанного пучка вычисляется по формуле:

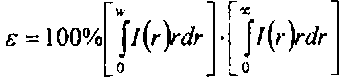
Для того, чтобы найти фазу радиально-симметричного ДОЭ ф(р), р²=х²+у², который формирует заданное распределение интенсивности 1^ в фокальной плоскости линзы нужно решить интегральное уравнение:

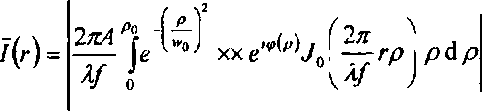
где ф(р) - искомая фаза ДОЭ, / - фокусное расстояние после линзы, Ае '^1у - амплитуда исходного коллимированного гауссового пучка с радиусом Wo, J(K^ - функция Бесселя нулевого поряд ка, /(г) требуемое распределение интенсивности. В нашем случае оно выбирается постоянным:

^По^о^Г

где R_o - радиус дифракционного пятна, который меняется в ходе численного моделирования.

Уравнение (36) решалось итеративно, методом последовательных приближений. Параметры расчета были выбраны следующие: w₀ = 3.63 мм, / = 654 мм, X = 0.488 мкм, w = 0.028 мм. Начальная оценка фазы ф(р) выбиралась нулевой. В ходе численного моделирования оказалось, что с увеличением радиуса дифракционного пятна R_o в выходной плоскости происходит выравнивание интенсивности /(г) за счет “растекания” за круг радиуса ж На рис. 6 приведены зависимости ошибки (рис.ба) и эффективности (рис.66), рассчитанные по формулам (34) и (35). Видно, что при R₀ изменить ничего не удается: параметры 5 и е почти не изменяются. Изменения начинают происходить при R₀>w. При этом максимального выравнивания интенсивности в пятне (минимальной ошибки 6=3.8%) удается достигнуть при выборе R^ I .64w. При этом эффективность опускается с уровня 86% до 55%. Для каждого ра-

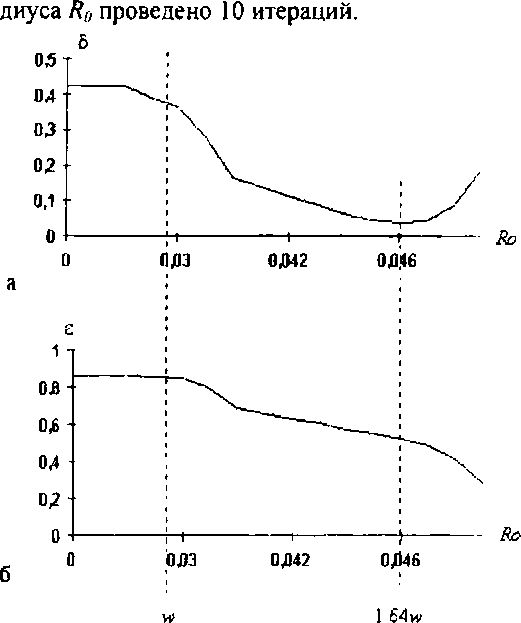
Рис. 6. Зависимость среднеквадратичной ошибки выравниваемой интенсивности гауссового пучка (а) и доли энергии в .минимальном дифракционном пятне радиуса w (б) от радиуса .моделируемого пятна R_o

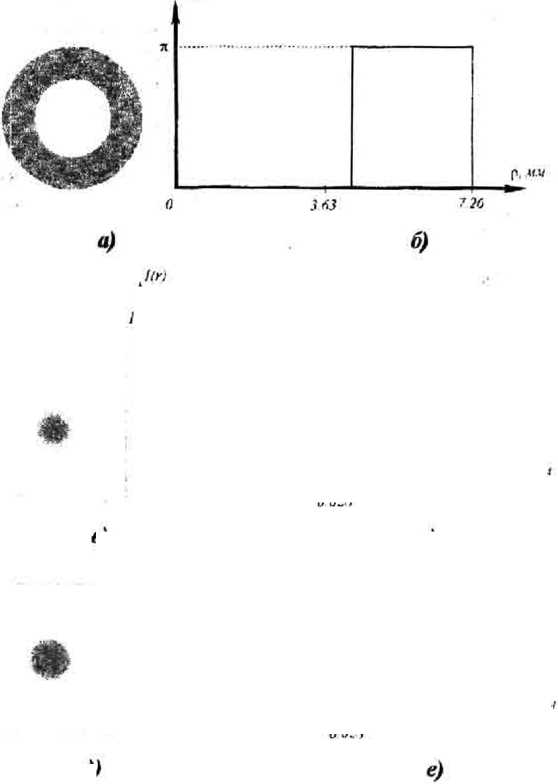
На рис. 7 показан оптимальный вариант расчета данным метолом. В отсутствии ДОЭ на выходе системы получается гауссовое пятно (рис. 7в), распределение интенсивности в котором (кривая 1, рис. 7г) отличается от постоянного значения (кривая 2, рис. 7г) на 8=46%, а в круге радиуса и=0.028 мм заключено при этом в=86% от всей энергии пучка.

Если в коллимированный гауссовый пучок поместить ДОЭ, рассчитанный данным методом, би- парная фаза которого показана на рис. 7а (се сечение показано на рис. 76, скачок фазы на к имеет место в точке Я,—4.4 мм), то на выходе системы получится световое пятно (рис. 7д), распределение интенсивности в котором (кривая 1, рис. 7е) будет отличным от постоянного значения (кривая 2, рис. 7е) на 6%, а в круге радиуса и=0.028 мм будет при этом заключено 61% от всей энергии пучка.

Таким образом. методом решения интегрального уравнения (36) удается за счет снижения энергетической эффективности на 24% (с 86% до 61%) выравнить гауссовый пучок с точностью 6% (ошибка упала с 46% до 6%).

Заметим, что форма кривой 1 на рис. 7е существенно отличается от гауссовой. Гауссовый пучок, отличающийся на 6% от постоянного значения в круге радиуса w=0.028мм, оставил бы только 34% своей энергии в этом круге.

Vp>

<9

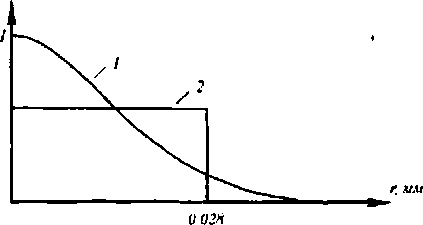
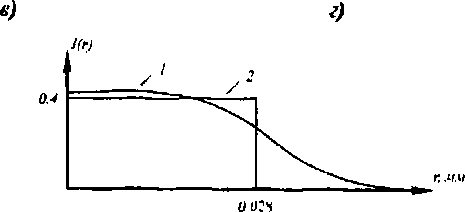
Рис. 7. Формирование круглого пятна с помощью ДОЭ и линзы, расположенных в перетяжке гауссового пучка; фаза ДОЭ (а) и ее радиальное сечение (б), интенсивность гауссового пучка на выходе без ДОЭ (в) и ее сечение (г), интенсивность выровненного гауссового пучка в присутствии ДОЭ (д) и ее сечение (е)

В этом разделе показано, что изменение радиуса R_o минимального дифракционного пятна в формуле (37) при решении ур. (36) приводит к бинарному виду фазовой функции ДОЭ. Причем интерес представляет случай, когда на апертуре ДОЭ имеется только один скачок фазы на л.

Заметим также, что соотношение радиуса скачка фазы ДОЭ для оптимального случая Я/=4.4мм и радиуса амплитуды гауссового пучка и0=3.63мм составляет ^у = 0.825 > Vo^ » 0.707 , то есть представляет тот случай (22), когда имеется небольшой локальный минимум в центре (сравните рис. 461 и рис. 7е).

• 5.    Моделирование для неколлимированного гауссовского пучка

• 5.1.    Формирование круглого пятна

В этом разделе при моделировании рас-смат-ривалась оптическая система, приведенная на рис. 1, когда ДОЭ располагается на некотором расстоянии от перетяжки гауссового пучка. В данном случае анализ проводился по двум параметрам: изменялся радиус фазового скачка на ДОЭ и его местоположение (расстояние от перетяжки гауссового пучка).

Параметры численного моделирования: радиус перетяжки гауссового пучка w_o=0.1 мм: длина волны аргонового лазера: 2л/к = 0.488 мкм; /= 10 мм -фокусное расстояние линзы; расстояние от перетяжки до линзы z=l60 мм. На рис. 8 показано в полутонах (негатив) двумерное распределение интенсивности в фокальной плоскости линзы для гауссового пучка без ДОЭ (а) и его радиальное сечение (б). Радиус фокального пятна по уровню 60% равен 0.008 мм (рис. 86). Также показана двумерная картина дифракции (негатив) в фокальной плоскости линзы в присутствии ДОЭ (рис. 8в) и радиальное распреде-

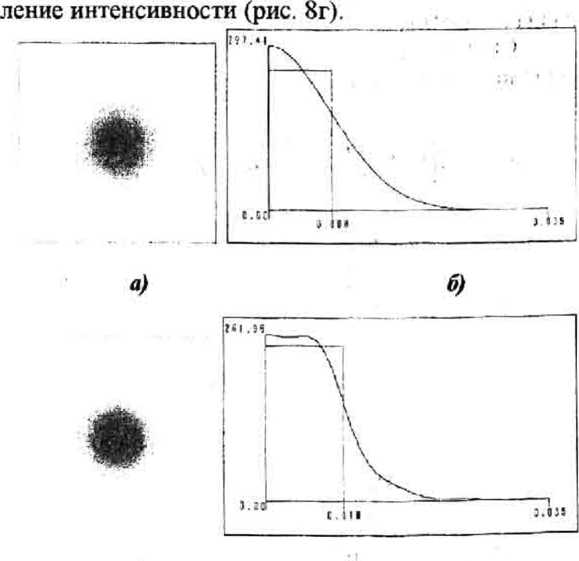
1*ис. 8. Формирование круглого пятна с помощью ДОЭ и линзы, расположенных на расстоянии от перетяжки гауссового пучка; интенсивность гауссового пучка на выходе без ДОЭ (а) и ее сечение (б), интенсивность выровненного гауссового пучка в присутствии ДОЭ (в) и ее сечение (г)

В этом случае радиус скачка фазы ДОЭ был равен 2^=0.381 мм, а радиус гауссового пучка непосредственно перед линзой равен и=0.267 мм. Их отношение равно 1.422. Это число немного больше, чем предсказывает формула (24), что означает отсутствие локального минимума в центре. Однако, как видно из рис.8г локальный минимум, хоть и не в центре, все же имеется. Такое различие картин 4а и 8г появляется из-за расходящегося волнового фронта гауссового пучка на расстоянии, куда теперь помещен ДОЭ. Доля световой энергии в круге радиуса 0.01 мм (по уровню 60%) составляет 59.1% от всей энергии гауссового пучка. Это число несколько меньше, чем предсказано формулой (28). Это также связано с тем, что в численном эксперименте гаус-совый пучок неколлимированный, и на линзу падает расходящийся волновой фронт. Относительная средняя квадратичная ошибка отклонения распределения интенсивности фокального пятна в данном круге от постоянного значения равна 10%.

Моделирование показало, что размещение комбинации ДОЭ+линза с тем же радиусом скачка А_;=0.381 мм в других местах на оптической оси приводит к падению энергетической эффективности. На рис. 9 показана зависимость энергетической эффективности в круге радиуса по уровню 60% от расстояния между' перетяжкой гауссового пучка и ДОЭ+линза. Параметры пучка такие же, как для рис.8. На рис.9 видно, что максимальная эффективность выравнивания интенсивности дифракционного пятна достигается при 150 мм <  г < 160 мм. Заметим, что френелевская длина в данном случае

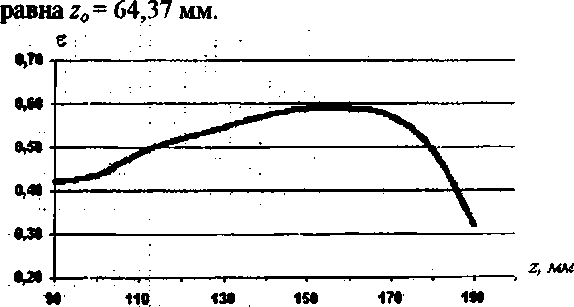
Рис, 9. Зависимость энергетической эффективности в круге радиуса Ко.< по уровню 60% максимальной интенсивности от расстояния г между перетяжкой гауссового пучка и ДОЭ+линза

• 5.2.    Формирование квадратного пятна

В гауссовом пучке на расстоянии z от его перетяжки, радиус которой w0, располагается фазовый ДОЭ с функцией пропускания ткзМ \9

х <  2R_p у < 2Rj х|>2Л₇,|> >2R_j

IRj - величина стороны квадратной фазовой ступеньки.

Параметры z и R, требуется найти, чтобы обес печить нужные характеристики гауссового пучка в фокальной плоскости сферической линзы с фокус-ным расстоянием f

Если на расстоянии z от перетяжки расположить ДОЭ с пропусканием (1), а за ним расположить линзу, то вблизи задней фокальной плоскости линзы сформируется комплексная амплитуда света

^> п- Д?)=A JI ^о к у. *W> д') ^х

-V ik^z ( i з хехр~^'Х + У

) х ехр --у(х^ + w/) dxdy, (39)

где |Дд| « / - малое расстояние от фокуса: Az<0 - до фокуса, Az>0 - после фокуса.

Аналитически интеграл (39) вычисляется с помощью функций Ломелля. Анализ его затруднителен. Поэтому ниже приводятся результаты численного моделирования.

Параметры моделирования: 2=0.488 мкм, м_й = 0.1 мм. г = 230 мм, радиус амплитуды гауссового пучка на этом расстоянии в- = 0.37 мм. 6 -я - скачок фазы ДОЭ, /= 17 мм - выбрано таким образом, чтобы радиус гауссового пучка в фокусе (Az=0) по спаду' интенсивности в е² раз был равен 0.028 мм.

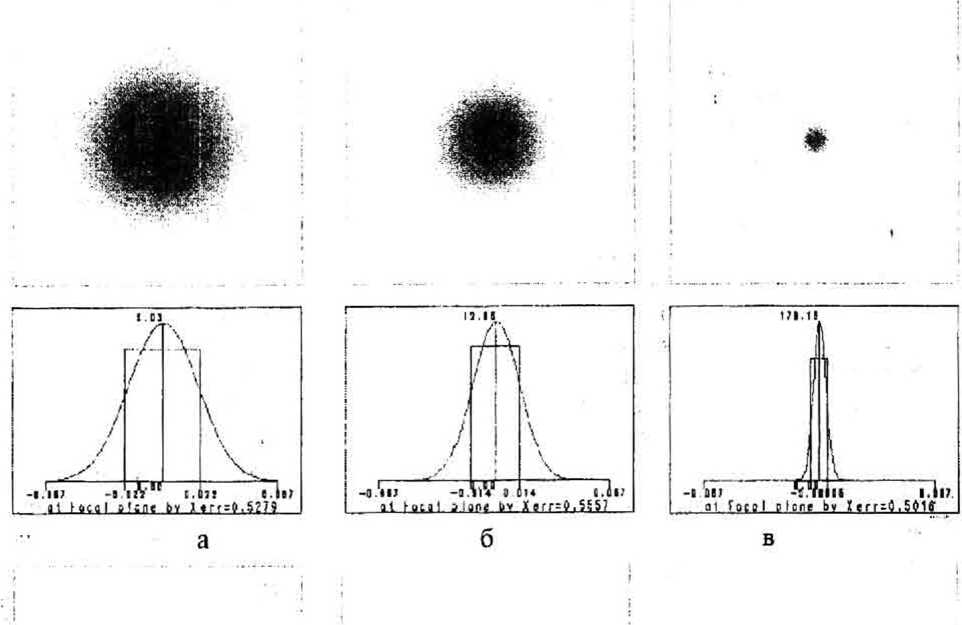
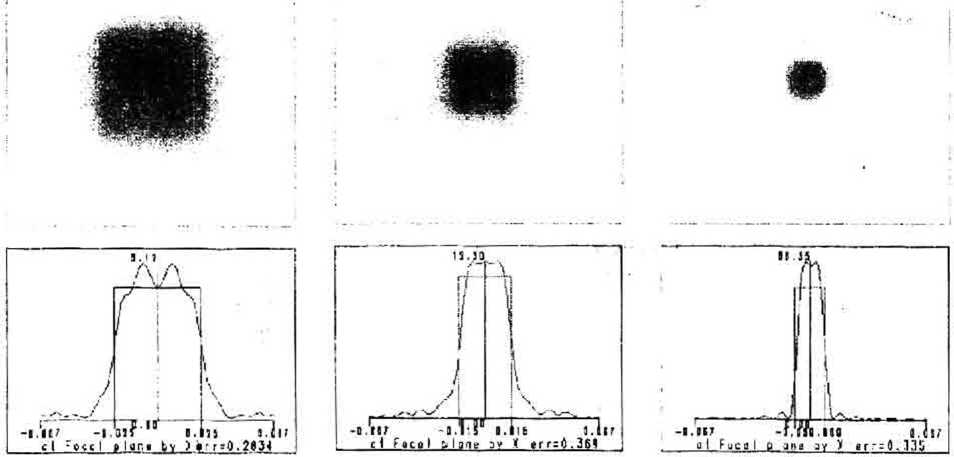
На рис. 10 показаны картины дифракции света на разных расстояниях от фокальной плоскости линзы, полученные без ДОЭ и в присутствии ДОЭ, а также их радиальные сечения, на которых отмечены радиусы по спаду интенсивности в 0.6 раз. На рис. 106 показана картина дифракции в фокальной плоскости (z4z=0) для гауссова пучка без ДОЭ. В круг радиуса Яо^О-ОМ мм попадает Ееу=39.3% всей энергии пучка. Максимальная интенсивность в пучке на оси равна /тю=12.5б.

На рис.Юа и Юв показаны дифракционные картины для гауссова пучка без ДОЭ до фокуса (рис.Юа: zk=-0.2 мм) и после фокуса (рис. Юв: Jz=0.4 мм). На расстоянии Jz=0.4 мм после фокальной плоскости происходит максимальная концентрация энергии гауссова пучка (/,„„=170.18, а Яо.6=0.005 мм). До фокуса (рис.Юа. dz=-0.2 мм) гаус-совый пучок еще шире, чем в фокусе (R_{o 6}=0.022 мм) и максимальная интенсивность еще меньше (/^=6.03). Заметим, что эффективность во всех случаях примерно одинакова: Ej)* = 39.9% (рис.Юа). 39.3% (рис. Юб), 38.9% (рис. Юв).

Далее приведем дифракционные картины, полученные на тех же расстояниях для гауссового пучка в присутствии ДОЭ (38). На рис. 1 Од показано распределение в геометрическом (|юкусе линзы (zlz=0): максимальная интенсивность /,„„=12.30 (это несколько меньше чем на рис. 106: /_тах= 12.56); половина стороны квадрата /<0 6=0.015 мм (это немного больше чем на рис.106: Яог,⁼О.О14); доля энергии в квадрате со стороной Ro ₆ равна ЕД=6^.2% (это больше на 20%, чем соответствующая эффективность на рис. Юб: ^39.3%).

На рис. 10с показана картина дифракции в плоскости максимальной концентрации энергии [Тучка (Jz=0.4 мм): R_(J 6=0.009 мм (почти в два раза (больше, чем на рис.Юв: Я_О6⁼О.ОО5 мм); /„,„=56.35 (почти в 3 раза меньше, чем на рис. Юв: /_П|„= 178.18); £Д' = 65.2% (на 27% больше, чем на рис.Юв: ЕД = 38.9%).

Из сравнения попарно рисунков 106 и 10д, а также 10в и 10е можно сделать вывод, что имеются две плоскости, в которых преобразование круглого пучка в квадратный происходит по разному.

В плоскости максимальной концентрации энергии пучка (минимальный дифракционный радиус) параметры гауссового и квадратного пучков приведены в Таблице 1.

В плоскости геометрического фокуса линзы такая таблица будет выглядеть по другому (см. Табли-ЦУ 2).

На рис. Юг показана картина дифракции в присутствии ДОЭ до фокуса Az=~0.2mm. В этой плоскости достигается максимальная эффективность преобразования: EjJ= 67.5% (это на 27% больше, чем на рис.10г:£#=39.9%).

г-д   е

Рис. 10 Формирование квадратного пятна с помтцыо ДОЭ и линзы, расположенных на расстоянии от перетяжки гауссового пучка: интенсивность гауссового пучка и сечение на выходе без ДОЭ: до геометрического фокуса линзы Ьг=-0.2мм (а), в фокусе &г=0 (б) и в плоскости максимальной концентрации энергии Лг=0.4мм (в); интенсивность выровненного гауссового пучка и сечение в присутствии ДОЭ: до геометрического фокуса линзы Ьг=-0.2мм (г), в фокусе Аг=О (д) и в плоскости максимальной концентрации энергии \г=0.4мм (е).

В Таблице 3 показано как изменяются параметры гауссового пучка в плоскости геометрического фокуса (при Jz=O) при различных значениях стороны квадратной ступеньки ДОЭ Rj. Обозначения: R(_V6 - половина стороны квадратного сечения гауссового пучка по уровню 0.6 от интенсивности в центре 7(0), Eff - это доля энергии попадающая в квадрат со стороной 2Ro6.

Из таблицы видно, что максимальная эффективность EJJ = 60% достигается при /^=0.41 мм. Отношение оптимального размера половины ширины фазовой ступеньки ДОЭ для формирования квадрата и радиуса амплитуды гауссового пучка в плоскости ДОЭ и' = 0.37 мм составляет величину

• 1 .11, что меньше соотношения, определяемого (24) V? к 1.41 для формирования круга.

Таблица 1.

Сравнение гаусеового и выровненного пучков в плоскости максимальной концентрации энергии (Бж=0.4 мм).

	гаусс	квадрат
Ям	0.005 мм	0.009 мм
	178.18	56.35
_Ш	38.9%	65.2%

Таблица 2.

Сравнение гаусеового и выровненного пучков в плоскости геометрического фокуса линзы (Az=O)

	гаусс	квадрат
Бо.б	0.014 мм	0.015 мм
	12.98	12.30
	39.3%	60.2%

Таблица 3.

Параметры гаусеового пучка в плоскости геометрического фокуса (Аг=0) при различных значениях стороны квадратной ступеньки ДОЭ Rj

		/(0)	Eff MB
0.05	0.012	12.058	0.237
0.10	0.008	11.158	0.104
0.15	0.007	16.844	0.119
0.20	0.007	27.949	0.196
0.25	0.007	38.349	0.237
0.30	0.007	38.757	0.231
0.35	0.008	28.010	0.201
0,40	0.014	15.287	0.531
			^ЭнЁйбйй
0.42	0.015	10.145	0.602
0.45	0.014	8.536	0.564
0.49	0.015	9.780	0.558
0.50	0.017	11.022	0.561
0.55	0.015	14.359	0.325
0.6	0.014	14.230	0.323
0.65	0.014	12.613	0,403

Заключение

В данной работе получены следующие результаты:

• -    показано, что для эффективного выравнивания распределения интенсивности в сфокусированном гауссовом пучке можно использовать простые ДОЭ в виде квадратной или круглой ступенек, которые осуществляют фазовую задержку в полдлины волны, а радиус - в V2 раз (для крута) больше радиуса амплитуды гаусеового пучка в плоскости ДОЭ;

• -    предложена модель для выравнивания интенсивности гаусеового пучка с помощью амплитудной маски типа ’’мексиканской шляпы", которая предсказывает оптимальный радиус скачка фазы

ДОЭ на я, а также значение эффективности в круге радиуса, определяемого по спаду интенсивности на 40% от максимального значения (0.6^);

- показано, что с помощью фазового ДОЭ в виде квадратной или круглой ступеньки можно выровнять интенсивность в сфокусированном гауссовом пучке с ошибкой 10% в области падения интенсивности на 40% ф.6-1_тах), радиус этой области почти в 2 раза больше, чем радиус гаусеового пучка, а попадает в эту область около 60% всей энергии.

Эта работа выполнена при поддержке Российского фонда фундаментальных исследований (№№ 96-15-96026, 98-01-00894).