Высокоэффективная криотемпература

Во многих случаях непосредственное измерение температур в опочных объемах энерготехнологических агрегатов затруднено. В этой связи большое значение для инженерных расчетов лучистого теплообмена имеют аналитические зависимости, описывающие распределение температур в неизотермических объемах рабочих сред. При описании распределения температур неизотермических сред собственное излучение неоднородной среды заменяется гипотетическим излучением однородного изотермического объема. В топочных пространствах и газоходах вследствие сильной загрязненности поверхностей нагрева граничные поверхности являются отражающими и излучающими. Кроме этого, около поверхностей нагрева всегда имеется слой газа с более низкой по сравнению с центром объема температурой.

В качестве параметра при корректном описании температурного поля неизометрических объемов при расчетах лучистого теплообмена принята эффективная температура Т_э ф При простейших инженерных расчетах в качестве эффективной температуры принимают среднеарифметическую Т са , среднегеометрическую Т сг температуры:

Т са = (Т ст +Т ц )/2,                   Т сг = (Т ст ·Т ц )^0,5                (1)

где Т ст, Т ц – температуры стенки и центра поперечного сечения неизотермического объема газохода.

Более строгий учет селективности свойств газовой среды и не изотермичности при определении эффективной температуры может быть выполнен исходя из решения уравнения переноса монохроматического полусферического излучения в плоском слое неизотермической среды при наличии отражающих и излучающих граничных поверхностей. Удобным является использование понятия приведенной эффективной температуры θ_э ф , которое позволяет исключить из рассмотрения при анализе конкретных расчетов длину волны λ. В окончательном виде формула для эффективной приведенной температуры двухфазной среды, полученная К.С. Адзерихо, Е.Ф. Ноготовым, В.П. Трофимовым [28], записывается в виде: θ эф = λТ эф = с 2 (ln(1+1/А))^-1,          (2)

τ0

где А = (К/(1–exp(–Кτ 0 )) ∫ exp(–К(τ 0 – τ)))/(exp(с 2 /λΤ(τ)) –1); 0

К = 2(1-Sc)^0,5; с 2 – вторая константа излучения Планка; τ 0 ,τ'– конечное и текущее значения монохроматической плотности (оптической плотности); S c – критерий Шустера.

Конкретное распределение температур по поперечным сечениям газоходов для неизотермических объемов может быть описано в зависимости от оптической толщины τ одним из следующих выражений, заданных аналитически: θi (τ)=λТi (τ), i=1,2,…,8.

Первое из этих выражений характеризует собой распределение температур в установившимся турбулентном потоке (профиль Шлихтинга) (рис. 1):

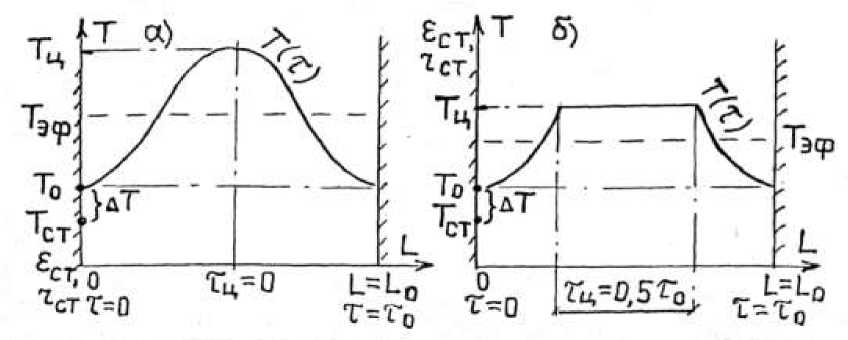
Рис. 1. Распределение температур по поперечным сечениям газоходов: а – профиль Щлихтинга, б – профиль с центральным изотермическим ядром θ 1 (τ) = θ ст +(θ ц – θ ст ) [1-(1-2τ/τ 0 )^1,5]^1,6.                        (3)

Представленные схемы профилей и конкретных экспериментальных распределений температур по поперечным сечениям газоходов, показывают, что для энерготехнологических агрегатов наиболее характерными являются профили с центральным изотермическим ядром при Т ц /Т ст = 1,4–2,6.

Расчеты с использованием формулы (1) , что при τ0>5 с увеличением критерия Шустера Sс от 0 до 0,6 эффективная приведенная температура θэф возрастает в среднем на 11 %. При τ0>5 влияние критерия Шустера Sс на θэф становится меньше. С ростом полки изотермического ядра τц от 0 до 0,5τ0 при τ≥5, Sc=0, θэф уменьшается на 22%. При дальнейшем увеличении τц уменьшение θэф замедляется. Увеличение отношения θэф/θст от 1,4 до 2,6 приводит к росту θэф в среднем на 5 % при температуре центра θц=3·103 м·К, где θст – приведенная температура стенки. Для удобства анализа можно представить среднеарифметическую Тса и среднегеометрическую Тсг температуры в виде условных приведенных температур: θса=λТса, θсг=λТсг. Сравнение θэф=λТэф, с θса=λТса и θсг=λТсг показывает, что при небольших оптических толщинах τ0 до 5 и θц в области 3·10-3 м·К величины Тса и Тсг занижены в среднем на 25 %.

Для оптических толщин τ₀=15–20, Sc=0, τ_ц=0 и θ_ц/θ_ст>2 значения Т_са, Т сг являются завышенными на 15–35%. Наименьшие расхождения (в среднем 10%) между Т эф и Т са , Т сг в зависимости от размеров центрального ядра наблюдаются в области τ₀=5 при τ_ц=0. В области больших оптических толщин τ 0 =15–20 и θ ц /θ ст =1,5-2 значения Т са и Т сг , в зависимости от размеров центрального ядра τ_ц, могут быть больше или меньше Т_э ф на 20-45%.

Размер центрального ядра τ_ц наиболее сильно влияет на θ_э ф /θ_ц при оптических толщинах около τ 0 =15 . Как и следовало ожидать, увеличение θ_ц/θ_ст вызывает снижение θ_э ф . Сопоставление результатов расчета Т_э ф для конкретных энерготехнологических агрегатов с расчетными данными других авторов для энергетических котлов показывает их хорошее согласование.

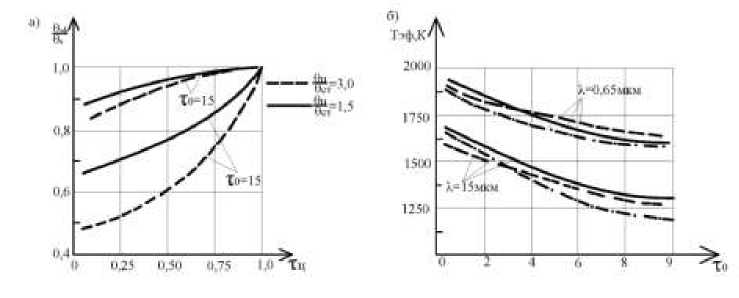
а) б)

Рис. 2.: а – зависимость θ_э ф /θ_ц от центрального ядра τ_ц при θ_ц=3·10^-3 м·К для различных τ 0 и θ ц /θ ст .; б – сопоставление Тэф при Тц=3·10^-3 м·К и Тц = 3·10^-3 м·К для Тц/Тст=2 с результатами, полученными другими авторами