Высокоэффективные рельефно-фазовые дифракционные элементы на криволинейных поверхностях вращения

В работе [1] для микроструктур дифракционных оптических элементов (ДОЭ), размещённых на пло- ских поверхностях раздела двух сред, приведены уравнения так называемых коррелированных рельефов. Эти рельефы микроструктур обеспечивают совпадающую с расчётной форму формируемого ДОЭ волнового фронта и 100% дифракционную эффективность на одной длине волны независимо от числа зон Френеля, а в случае двухслойных структур – близкую к 100% дифракционную эффективность в широком спектральном диапазоне. В настоящей работе получены уравнения коррелированных рельефов микроструктур однослойных ДОЭ, размещённых на криволинейных поверхностях раз- дела двух сред, и даны рекомендации по использованию этих уравнений при изготовлении двухслойных двухрельефных структур.

Фокусирующие и аберрационные свойства ДОЭ, как правило, описываются в рамках модели бесконечно тонкого фазового транспаранта, вносящего фазовую задержку в падающий на него волновой фронт. Одним из вариантов представления этой фазовой задержки для случая ДОЭ с кольцевой микроструктурой является используемый в программе оптического проектирования ZEMAX [2] степенной ряд J

Т ( р ) = m X A j Р 2 j ,                          (1)

j = 1

где m – номер рабочего дифракционного порядка, ρ – расстояние, отсчитываемое от оптической оси.

Оптическая сила ДОЭ определяется коэффициентом A ₁:

Ф =

m % A 1

п

а коэффициенты Aj при j =2; 3…; J являются ко- эффициентами асферических добавок. В выражении (2) % - расчётная длина волны, на которой задаются все коэффициенты Aj. В дальнейшем рабочим будем считать первый порядок дифракции, т.е. m=1.

В качестве криволинейной поверхности вращения оптического элемента, в котором будет выполняться рельеф путём удаления материала с его поверхности алмазным точением или травлением, может рассматриваться, например, «чётная» асферическая поверхность, описываемая в ZEMAX уравнением:

c р ² P_

z ( р ) =— _{7 7}⁺ X^a p р p , ⁽³⁾ 1 + 1 - - (1 + к ) С ² р ² p = 1

где z (ρ) – координата точки поверхности, отстоящей от оптической оси на расстояние ρ в системе координат, плоскость XOY которой касается вершины этой поверхности; c - кривизна поверхности в её вершине; к - коническая константа; a p при p =1; 2; „.; P - коэффициенты асферичности поверхности.

1.    Уравнения коррелированных рельефов микроструктур однослойных ДОЭ

Наиболее достоверную комплексную оценку работоспособности ДОЭ с точки зрения его функциональных возможностей даёт распределение интенсивности в картине дифракции Фраунгофера монохроматической световой волны на двух, установленных вплотную друг за другом оптических элементах. Одним из элементов является ДОЭ с рельефно-фазовой микроструктурой, а вторым – эталонный бесконечно тонкий фазовый транспарант, вносящий фазовую задержку, равную по величине требуемой, но имеющую противоположный знак [1]. Сразу же отметим, что фазовая задержка бесконечно тонкого транспаранта в соответствии с уравнением (1) является гладкой и может быть как положительной, так и отрицательной. Что же касается фазовой задержки, вносимой коррелированным рельефом ДОЭ, то она, будучи подобной фазовой задержке эталонного транспаранта, является кусочнонепрерывной и испытывает скачки на границах зон Френеля. Здесь отметим, что применительно к рельефно-фазовому ДОЭ с линейно-пилообразной или коррелированной микроструктурой под термином «зона Френеля» понимается участок элемента, в пределах которого фазовая задержка, вносимая элементом в падающий на него волновой фронт, изменяется от 0 до 2 п [3, 4].

Предположим сначала, что коррелированный рельеф ДОЭ выполняется на криволинейной поверхности выпукло-плоской линзы, на выпуклую поверхность которой падает из воздуха коллимированный световой пучок нормально к вершинной касательной плоскости этой поверхности. Направление распространения света выбрано совпадающим с направлением движения обрабатывающего инструмента, приближающегося к криволинейной поверхности заготовки. Осевую толщину линзы положим равной d, и тогда (см. рис. 1 а) длина оптического пути на расчётной длине волны X от вершинной касательной плоскости к криволинейной поверхности, имеющей рельефную структуру, до плоской поверхности линзы будет равна lCR = h(Р) + nX[d - h(Р)] = nхd - (nX - 1)h(P) ’ (4)

где h (p) - глубина рельефа, отсчитываемая от вершинной касательной плоскости криволинейной поверхности; n х - показатель преломления материала структуры ДОЭ на расчётной длине волны.

Если же рельеф на криволинейной поверхности отсутствует, но на неё нанесён эталонный фазово-задерживающий слой, то выражение для оптического пути между указанными плоскостями будет иметь вид lрт—^^^(р)+z(р)+n х[d- z(р)]= = 2п^(р) + n _ d -(n х- i)z (р)

где фазовая задержка эталонного транспаранта T(p) и координата точки криволинейной поверхности z (p) могут описываться, например, уравнениями (1) и (3).

Здесь заметим, что, как видно из уравнения (3), при a p =0 знак координаты точки поверхности z ( р ) совпадает со знаком кривизны при вершине поверхности c , выбираемым в соответствии с правилом знаков, принятым в оптике: величины c и z (p) положительны, если центр поверхности находится после неё по направлению распространения света. Аналогичное правило в настоящей статье принято и для знака глубины рельефа. Она считается положительной, если, отсчитываясь от вершинной касательной плоскости, совпадает с направлением распространения света (см. рис.1 а ).

Искажения волнового фронта, обусловленные рельефно-фазовой микроструктурой ДОЭ, можно оценить по разности оптических путей, определяемых выражениями (4) и (5), т.е.

^A l ^— l CR

^^^^^^e

l рт = ( nx - 1) [ z ( р ) - h ( р ) ] -;^Х^ ( р ). (6) ^X                  2 n

Для того чтобы изображение, формируемое ДОЭ на расчётной длине волны, было дифракционноограниченным, а дифракционная эффективность равна 100%, необходимо обеспечить постоянство разности оптических путей в пределах каждой зоны

Френеля и её скачкообразное приращение на X от зоны к зоне. В случае T(p)<0 это условие имеет вид

Al — (i - 1)X ,

а при T(p)>0 записывается как

Al — -iX .                                          (8)

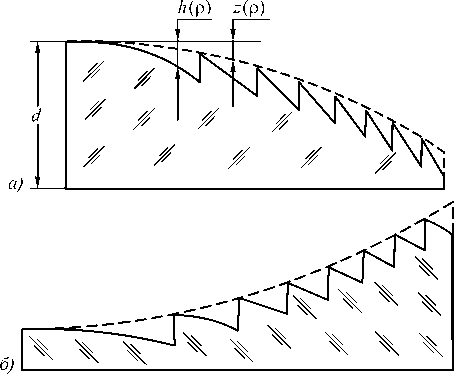
Рис. 1. Рельефно-фазовые микроструктуры ДОЭ на асферической поверхности: а) при ^(р) <0 и z(р) >0; б) при ^(р) >0 и z(р) >0; в) при ^(р) <0 и z(р) <0;

г) при ^М >0 и z ⁽р ) <0

В формулах (7) и (8) i - номер зоны Френеля, определяемый текущим значением расстояния от оптической оси в соответствии с условием р i - 1 < р < р i . В этом условии р i - 1 и р i - внутренний и внешний радиусы, ограничивающие i - ю зону Френеля [для центральной, т.е. первой ( i =1) зоны Френеля р ₀=0]. Радиусы, ограничивающие зоны Френеля, являются действительными и положительными корнями уравнения

| *(р)| — 2пi. (9)

Из уравнения (6) с учётом формул (7) и (8) нетрудно получить глубины коррелированных рельефов ДОЭ:

и

h ( p ) = z ( p ) - H

i - 1 + ± T⁽p ) 2 n

при ^ ( p ) <0

- i +    G T ( p )

2 n

h (p)= z (p)- H

- i+*(p) 2n

при ^ ( p ) >0.

В формулах (10) и (11) H – толщина рельефного слоя, т.е. модуль максимальной глубины рельефа [3]:

H = ^X/ ( ⁿ X^{- 1 )} -

Легко видеть, что уравнения рельефов (10), (11) справедливы и в случае выполнения рельефов в вогнутой криволинейной поверхности, когда z (ρ)<0 (см. рис. 1 в и рис. 1 г ). Более того, эти же формулы, но при z (ρ)=0 дают глубину рельефа, отсчитываемую от исходной поверхности, т.е. глубину съёма материала на этапе формирования дифракционной микроструктуры.

2. Уравнения коррелированных рельефов микроструктур двухслойных двухрельефных ДОЭ

Высокой дифракционной эффективности рельефно-фазовых дифракционных микроструктур в

пределах заданного спектрального диапазона достигают, используя несколько рельефных слоёв из оптических материалов, отличающихся дисперсией. При этом наибольший практический интерес представляет двухслойная структура с двумя рельефами [5] (см. рис. 2). При переходе к двухслойной структуре с двумя рельефами выбираются оптические материалы слоёв и определяется толщина рельефа каждого из слоёв H 1 и H 2 , обеспечивающие предельно высокую дифракционную эффективность в заданном спектральном диапазоне ( X min , X max ) .

h 2 ⁽p ) = z ⁽p^{)- (} H 1 ^- H 2 )

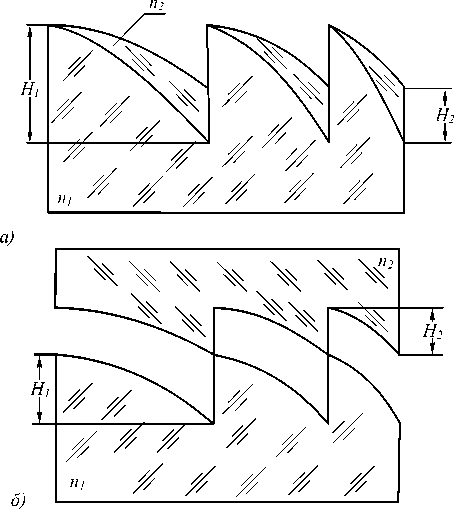
Рис. 2. Двухслойные микроструктуры с коррелированным

Величины H 1 и H 2 могут быть получены либо приближенно аналитически (см., например, [7]), либо численным методом, но более точно, как это предложено в [6]. В случае двухслойной структуры с внутренним и наружным рельефами (рис. 2 а ) уравнения рельефов ДОЭ зависят не только от знака функции Ψ(ρ) (как это было у однослойной структуры), но и от соотношения показателей преломления n ₁ и n ₂ слоёв структуры, что можно учесть, как это сделано в работе [1], с помощью величины G = sgn ( 1 - п1 /п ₂ ) . В результате, при G ^ ( p ) <0 глу-

рельефом, обеспечивающие высокую дифракционную эффективность в широком спектральном диапазоне (показан случай, когда ^ ( p ) <0 и П 1 <  п 2 ): а) структура с внутренним и наружным рельефами;

б) структура с двумя внутренними рельефами

В случае двухслойной структуры с двумя внутренними рельефами (рис. 2 б ) уравнение рельефа нижнего слоя (с текущей координатой исходной криволинейной поверхности z 1 (ρ), толщиной слоя Ψ(ρ) и его показателем преломления n ₁ ) совпадает по форме с уравнениями (11) и (12).

При ^ ( p ) <0

h1 (p) = z 1 (p)- H1

и при ^ ( p ) >0

h1(p) = z1(p)- H1

бины рельефов каждого из двух слоёв описываются

уравнениями

hi (p)= z (p)- H1

i - 1 +    G T ( p )

2 n

и

h 2 ( p ) z ⁽p^{)- (} H 1 ^- H 2 )

i - 1 + G T ( p ) 2 n

а при G T ( p ) >0 - уравнениями

h1 (p)= z (p)- H1

- i + — G ^ ( p )

и

i - 1 +   ^ ( p )

2 n

-

i + y-^⁽p) . 2 n

Что же касается рельефа верхнего слоя (с текущей координатой исходной криволинейной поверхности z 2 (ρ), толщиной слоя H 2 и его показателем преломления n 2 ), то он, как легко видеть из рис. 2 б , с точки зрения изготовления является обратным (с точностью до толщины рельефа) по отношению к рельефу первого слоя. Текущая координата исходной криволинейной поверхности z ₂ ( p ) =- z 1 ( p ) , а глубина рельефа описывается уравнениями при Ψ(ρ)<0

h 2 ⁽p ) = z 2 ⁽p^)- H 2

-

i - ^ ( p ) 2 n

и при ^ ( p ) >0

h 2 ( p ) = z 2 ( p ) - H 2

i - 1 - 2^^T(P ) .

Нетрудно показать, что уравнения рельефов (13)(20), также как и уравнения (10), (11), справедливы и в случае выполнения рельефов в вогнутой криволинейной поверхности, когда z ( p ) <0. И, также как уравнения (10), (11), при z ( p ) =0 они дают глубину рельефа, отсчитываемую от исходной поверхности, т.е. глубину съёма материала оптического элемента на этапе формирования дифракционной микроструктуры.

Заключая раздел, отметим, что, как показано в работе [6], в спектральном интервале, охватывающем видимый и ближний ИК диапазоны, при отношении периода однослойной или двухслойной структуры к глубине микрорельефа к >  2,5 разница в значениях дифракционной эффективности и в оптимальных значениях максимальных глубин рельефов, получаемых в скалярном и бесконечно тонком приближении и методами, основанными на строгом решении системы уравнений Максвелла, весьма незначительна. Поэтому все результаты, получаемые в бесконечно тонком приближении, при к >  2,5 являются вполне надёжными.

Заключение

Теория коррелированного рельефа дифракционной микроструктуры, представленная в [1], распространена на структуры, выполненные на криволинейных поверхностях. Это, в частности, позволяет рассчитывать высокоэффективные гибридные рефракционно-дифракционные оптические системы, у которых на одной или нескольких сферических или асферических поверхностях рефракционных линз сформированы рельефно-фазовые микроструктуры дифракционных линз. Такие системы имеют более простую конструкцию, чем системы, содержащие только рефракционные линзы либо включающие помимо рефракционных линз и дифракционные линзы, микроструктуры которых выполнены на плоских поверхностях рефракционных линз или плоскопараллельных пластин. Упрощение конструкции оказывается возможным благодаря тому, что большее число эффективных коррекционных параметров позволяет существенно снизить уровень монохроматических и хроматических аберраций всех порядков (со всеми вытекающими отсюда позитивными последствиями) [8-12].

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках гранта Президента РФ для государственной поддержки молодых российских учёных № МД-2293.2012.9.