Высокоэффективный оптический элемент для светодиодных систем подсветки дисплеев

В настоящее время жидкокристаллические (ЖК) дисплеи повсеместно используются в мобильных устройствах, мониторах компьютеров, телевизорах. При этом разработка компактных, энергоэффективных систем подсветки ЖК-дисплеев является важнейшей задачей. В качестве источников света в системах подсветки ЖК-мониторов широко используются люминесцентные лампы с холодным катодом (ЛЛХК) [1, 2]. На рис. 1 показано сечение типичной системы подсветки дисплея, которая включает источники света (ЛЛХК), диффузный отражатель, диффузор.

диффузор

!«%*«*.*                                 »%*|

^диффузный отражатель

Рис. 1. Конструкция системы подсветки дисплея с люминесцентными лампами

Системы подсветки на основе ЛЛХК позволяют достичь высокой равномерности освещения, однако имеют ряд недостатков. В настоящее время более перспективными считаются светодиодные системы подсветки [3]. По сравнению с ЛЛХК светодиоды потребляют меньше энергии, имеют больший срок службы, устойчивы к вибрациям и ударам. В простейшем варианте ЛЛХК лампу заменяют линейкой (лентой) светодиодных источников.

В данной работе в качестве альтернативы к ЛЛХК предлагается светодиод со специальным преломляющим оптическим элементом (рис. 2). Оптический элемент имитирует ЛЛХК, формируя на диффузном

отражателе два симметричных, равномерно освещённых отрезка. На рис. 2 показан один из отрезков, формируемый правой половиной оптического элемента. Освещаемые отрезки становятся вторичными источниками света.

Отметим, что в настоящее время существуют материалы для диффузных отражателей, имеющие высокий коэффициент отражения в 95 –99% и закон рассеяния, близкий к закону Ламберта. Одним из материалов является материал spectralon, производимый компанией Labsphere Corporation [4, 5].

Для достижения высокой световой эффективности предлагается использовать оптический элемент, работающий по принципу полного внутреннего отражения. Отметим, что оптический элемент является осесимметричным (ось симметрии совпадает с освещаемым отрезком). Это обеспечивает простоту производства элемента.

диффузный отражатель

Рис. 2. Конструкция модуля светодиодной системы подсветки дисплея

Таким образом, набор ЛЛХК на рис. 1 может быть заменён набором светодиодов с оптическими элементами, фокусирующими в отрезки на диффузном отражателе. Предлагаемый подход позволяет создать компактные светодиодные системы подсветки дисплеев нового типа. Согласно представленным результатам моделирования, предложенный подход обеспечивает формирование равномерной освещённости в области с большим угловым размером (более 150° в направлении вдоль отрезков) при высокой световой эффективности в 94,5%.

Отметим, что расчёт преломляющего оптического элемента светодиода, фокусирующего в отрезок в

геометрии на рис. 2, впервые приведён в настоящей работе. Ранее элементы такого типа рассчитывались только с использованием приближения тонкого оптического элемента [6, 7].

1. Расчёт оптического элемента

Рассмотрим расчёт преломляющего оптического элемента для фокусировки в отрезок оcи Ox при точечном (компактном) источнике излучения (рис. 2). В силу симметрии будем рассматривать только правую часть элемента при x > 0 (рис. 3).

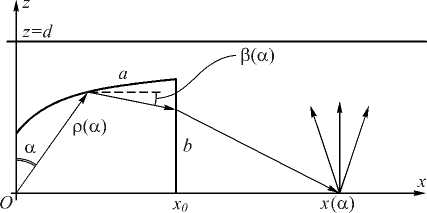
Рис. 3. Оптический элемент для фокусировки в отрезок оси Ox

полярный угол в плоскости Oyz , перпендикулярной плоскости рис. 3. Поскольку оптический элемент расположен при z >0, то фе[0, п]. В указанных координатах элемент телесного угла, соответствующий отрезку фе[0, п], имеет вид:

dQ(a) = пsin(п/2-а)dа .

Для записи закона сохранения светового потока необходимо приравнять световой поток, падающий на элемент d x освещаемого отрезка, к световому потоку от источника, излучённому в элемент телесного угла dQ(а). Таким образом, можно записать следующее равенство:

п sin(п/2-а) |/(а,ф)dф dа = E(x)dx,        (3)

IJ

где E ( x ), x e [ x 1 , x ₂] - заданная освещённость на отрезке, I (а, ф) - интенсивность источника излучения. Отметим, что корректное задание освещённости E ( x ) требует выполнения условия нормировки:

^а тах

п

Оптический элемент имеет ось вращения (ось Ox ). Профиль оптического элемента состоит из части а , работающей на эффекте полного внутреннего отражения (ПВО), и плоской выходной поверхности (часть b ), которая преломляет лучи после отражения от поверхности а . Мы пренебрегаем лучами, которые сразу падают на поверхность b .

Обозначим р(а) длину радиус-вектора точки профиля, где ае[0,атах] - угловая координата падающего луча (рис. 3). В работе [8] для р(а) получено следующее дифференциальное уравнение:

dp(a)    . ,    Гп/2-а-Р(а))

d. ' р " ct ^--------2 J,              (1)

J sin(п/2-а) jI(а,ф)dф dа = JE(x)dx.

0                             _ 0                     _            x i

При постоянной освещённости E ( x )= E ₀, x e [ x 1 , x ₂] проинтегрируем (4) и получим:

1 а x (а) = x +--jcos а

^E 0 0

п

JI (а, ф)dф dа .

0_

В случае ламбертовского источника, излучающего по оси Oz , интенсивность источника в координатах (а, ф) имеет вид:

I ( а, ф ) = I 0 cos а sin ф.

Подставляя (6) в (5), получим x (а) в аналитическом виде:

где функция Р(а) задаёт направление луча после ПВО (рис. 3). Из геометрии на рис. 3 несложно получить координату пересечения выходящего из оптического элемента луча с осью Ox в следующем виде:

x (а) = x 0 + |^р (а) cos (а)-

^- ( ^x 0

-р ( а ) sin ^(а) ) tg ( р ^(а) ) ]

Y¹ / ² ( а ) n ■ sin ( в ( а )) ’

где у(а) = 1 - ( n •sin ф (а)))², n - показатель преломления материала элемента. Определим функцию x (а) в правой части (2) из закона сохранения светового потока. Введём сферические координаты (а, ф), где ф -

2а + sin (2а)

x (а) = x +( x. - x I----------;—-—-.

maxmax

Подставим функцию x (а) в (2) и продифференцируем полученное уравнение по переменной а. В результате получим следующее дифференциальное уравнение:

dP(а)/ dа = F (а, Р(а), р(а), р‘ (а), x '(а)),(8)

где

F ( а, Р, р, р', x ' ) = 2

n sin (в(а)) x '(а)у1/2 (а) + sec (р(а))у(а)( sin (а-Р(а))р(а)- cos (а-Р(а))р'(а

n2 sec (в(а)) sin (2р(а))(x0 sin (р(а))- cos (а -Р(а))р(а))- 2у (а)g (а)

g (а) = x 0tg2 (в(а)) + ( cos (а) ctg (в(а))-sin (а) tg2 (в(а)))р(а).

Производная р'(а) , входящая в правые части в (8), (9), определена в уравнении (1). Производная x'(а) в правой части в (8), (9) может быть получена из уравнений (5) или (7). После подстановки указан- ных выражений для производных ρ′(α) и x′(α) в (8) правая часть (8) будет зависеть только от переменной α и функций β (α), ρ (α). Таким образом, расчёт оптического элемента для формирования отрезка с заданной освещённостью сведён к интегрированию системы двух обыкновенных дифференциальных уравнений (1), (8), разрешённых относительно производных. Указанная система может быть проинтегрирована с использованием стандартных численных методов (например, метода Рунге–Кутты).

В рамках рассматриваемого подхода предполагается, что оптический элемент формирует освещённый отрезок на диффузном отражателе. При этом освещаемый отрезок будет вторичным источником излучения.

2.    Результаты численного моделирования

Разработанный метод расчёта оптического элемента был реализован в среде программирования Matlab [9]. На основе формул (1), (7)–(9) был рассчитан оптический элемент для равномерного освещения двух симметричных отрезков при ламбертовском источнике излучения. Для численного интегрирования системы дифференциальных уравнений (1), (8) использовалась функция ode45 из библиотеки Matlab. Расчёт был проведён при следующих параметрах: ρ(0) = 1 мм (расстояние от источника до поверхности оптического элемента по оси Oz ), α max =70° (угловой размер части a профиля на рис. 3), x 1 =50 мм, x 2 = 150 мм (координаты концов отрезка), показатель преломления материала элемента n = 1,493. Рассчитанный профиль правой половины элемента представлен на рис. 4. Габаритные размеры оптического элемента (правой части) по осям координат составляют 14,3 мм, 10,4 мм, 5,2 мм.

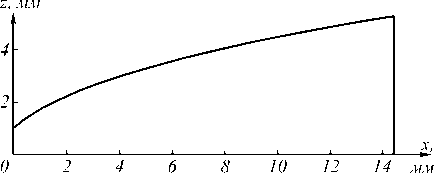
Рис. 4. Профиль оптического элемента (правая часть) для равномерного освещения отрезка оси Ox при ламбертовском источнике

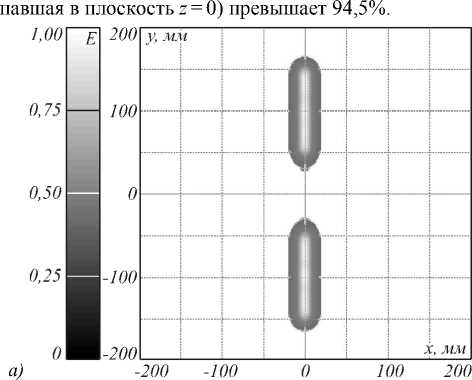
Для проверки правильности расчётов было выполнено моделирование работы рассчитанного оптического элемента в программе для светотехнических расчётов TracePro [10] (рис. 5).

На рис. 5а приведено полутоновое распределение освещённости, формируемое оптическим элементом в плоскости z =0, содержащей отрезки. На рис. 5б показан график распределения освещённости вдоль оси Ox. Распределения освещённости получены в программе TracePro при трассировке 200000 лучей и полностью соответствуют требуемому распределению (равномерное освещение двух отрезков с длинами 100 мм). Световая эффективность оптического элемента (доля излучённого светового потока, по-

0.75

0,50

0.25

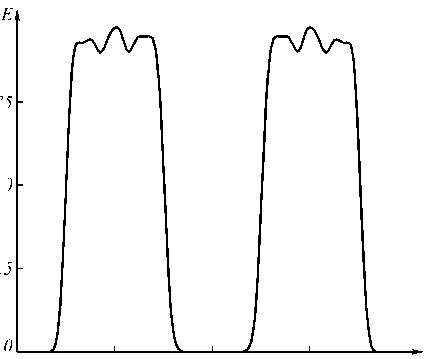
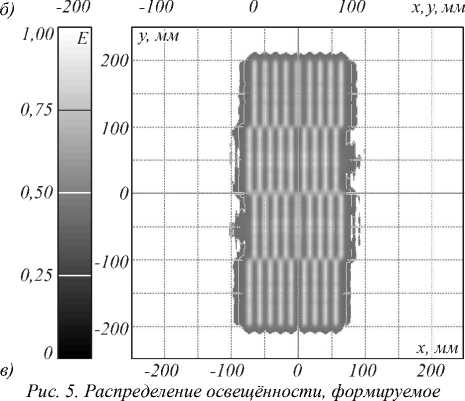
оптическим элементом для равномерного освещения двух отрезков в плоскости z=0 (правая часть профиля элемента показана на рис. 4) (а, б); распределение освещённости, формируемое двумя линейками оптических элементов (по 9 элементов в линейке) (в)

На рис. 5 в приведено распределение освещённости, формируемое матрицей из 18 оптических элементов (две линейки по 9 элементов). Оптические элементы в линейке отстоят на 16 мм. Линейки сдвинуты одна относительно другой на 8 мм по оси Ox и на 100 мм по оси Oy .

При использовании рассматриваемых оптических элементов в системе подсветки в плоскости z = 0 следует расположить диффузный отражатель. При этом конечной задачей является получение равномерного распределения света в некоторой плоскости z = d (рис. 3) над оптическим элементом.

Будем считать, что диффузный отражатель рассеивает в соответствии с законом Ламберта [4, 5]. В этом случае отрезки, формируемые в плоскости z = 0 (рис. 5б), являются вторичными ламбертовскими источниками. На рис. 6а, б представлены полутоновые распределения освещённости, формируемые в плоскостях z = 11,8 мм и z = 16 мм, в случае, когда плоскость z = 0 является ламбертовской отражающей по- верхностью.

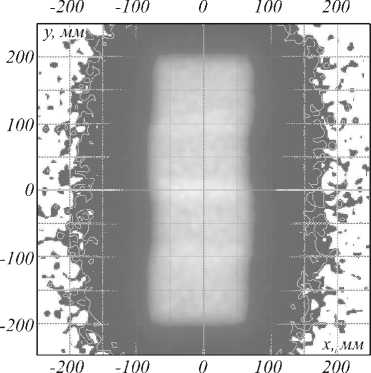
Рис. 6. Распределения освещённости в плоскостях z = 11,8 мм (а) и z = 16 мм (б), формируемые набором из 18 оптических элементов (две линейки по 9 элементов)

в случае ламбертовской отражающей поверхности

Распределения на рис. 6 рассчитаны в программном обеспечении TracePro® для рассмотренного выше набора из 18 оптических элементов (две линейки по 9 элементов). При этом при моделировании использовалось 200000 лучей для каждого источника. Рис. 6 показывает возможность получения равномерной освещённости на большой площади. Распределение освещённости в плоскости z = 11,8 мм (рис. 6а) является достаточно равномерным в пределах прямоугольной области с размером 350 мм на 100 мм. В то же время на рис. 6а ещё различимы отрезки, формируемые на диффузном отражателе. В плоскости z = 16 мм (рис. 6б) распределение становится ещё более равномерным, и отрезки уже неразличимы. Отметим, что расстояние между отрезками по оси Ox на рис. 5в также составляет 16 мм. Данный результат согласуется с результатами работы [11], где показано, что наибольшая равномерность освещённости достигается в случае, когда расстояние между ламбертовскими излучателями равно расстоянию до освещаемой плоскости. Таким образом, расстояние d между оптическими элементами (между отрезками) можно считать параметром, определяющим толщину оптической системы, то есть расстояние до выходной плоскости, на котором формируемое распределение освещённости будет равномерным.

Рассмотренный набор оптических элементов на диффузном отражателе можно рассматривать как фрагмент системы подсветки ЖК-дисплея. Увеличивая (или уменьшая) число элементов, можно равномерно осветить прямоугольную область заданного размера. Важно также отметить, что в отличие от стандартной системы подсветки на основе ЛЛХК (рис. 1) предлагаемая оптическая система не требует наличия внешнего диффузора.

Заключение

В работе предложен преломляющий оптический элемент светодиода для равномерного освещения двух отрезков на оптической оси. Оптический элемент является осесимметричным и прост в изготовлении. Расчёт оптического элемента сведён к интегрированию системы двух обыкновенных дифференциальных уравнений, разрешённых относительно производной.

Предложенные оптические элементы перспективны для применения в системах подсветки дисплеев. В этом случае отрезки формируются на поверхности диффузного отражателя и рассматриваются как вторичные линейные источники. Представленные результаты моделирования показывают возможность использования набора предложенных оптических элементов, расположенных на диффузном отражателе, для равномерного освещения прямоугольной области заданного размера с высокой световой эффективностью (более 94,5%).

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, грантов РФФИ 13-07-97001, 12-07-13113, 1207-31055, 12-07-31193 и соглашения 8027.