Высокоскоростные систолические отказоустойчивые процессоры цифровой обработки сигналов для инфотелекоммуникационных систем

Известно, что эффективность первичной обработки сигналов в современных инфокоммуника-ционных системах во многом предопределяется используемой математической моделью цифровой обработки сигналов (ЦОС). Реализации ортогональных преобразований в алгебраических модульных системах позволит не только повысить скорость и точность обработки сигналов, но и обеспечить отказоустойчивость вычислительного устройства ЦОС.

Постановка задачи исследования

Развитие телекоммуникационных технологий, появление новых систем передачи и обработки данных ставят перед проектировщиками (разра- ботчиками) и операторами сетей новые задачи по предоставлению новых услуг пользователям. С появлением средств мультимедиа и сетей с высокой пропускной способностью, обеспечивающих передачу мультимедийных данных в реальном масштабе времени, в современных информационных системах начинают применяться технологии, такие как видео и речевая связь, системы видеоконференций, голосовая почта, которые требуют обработки больших объемов данных. Как правило, в основу таких технологий положены методы и алгоритмы цифровой обработки сигналов.

Проведенные исследования [1-3] показали, что эффективность цифровой обработки сигналов во многом определяется математической моделью ортогональных преобразований сигналов. В настоящее время все множество известных моделей ЦОС и технологий их реализации можно разбить на две основные группы.

Основу первой группы составляют математические модели ЦОС, определяемые в поле комплексных чисел. Среди таких ортогональных преобразований можно выделить дискретное преобразование Фурье (ДПФ) и его быстрые алгоритмы (БПФ) [3]. Основным недостатком отмеченных моделей ЦОС является то, что в качестве поворачивающих коэффициентов используются иррациональные числа, что снижает точность вычислений. Кроме того, наличие двух вычислительных трактов (для обработки действительных и мнимых частей) негативно влияет на надежность функционирования спецпроцессоров (СП) цифровой обработки сигналов.

В основу второй группы положены математические модели ЦОС, реализуемые в конечных полях Галуа и обладающие свойством кольца и поля [1; 3-4]. Если значение входного сигнала x ( nT ) рассматривать как подмножество алгебраических систем, обладающих структурой кольца или конечного поля Галуа, то реализацию ортогональных преобразований сигналов можно свести к теоретико-числовым преобразованиям (ТЧП), определяемым в пространстве кольца вычетов целых чисел по модулю М [3].

Известно, что в подавляющем большинстве современных информационных технологиях задачи ЦОС сводятся к нахождению значений ортогонального преобразования конечной реализации сигнала для большого числа точек в реальном масштабе времени, что предопределяет повышенные требования к скорости и разрядности вычислительного устройства. Для эффективного решения данной задачи целесообразно перейти от одномерной обработки сигналов к многомерной в кольце полиномов. Такой переход к параллельной обработке сигналов базируется на изоморфизме, порожденном Китайской теоремой об остатках (КТО). В работе [5] доказана возможность реализации обобщенного ДПФ в кольце полиномов. При этом вычисления организуются в кольце полиномов P(z) с коэффициентами в виде элементов поля GF(p), представляющем собой сумму

P ( z ) = P 1 ( z ) + P 2 ( z ) + ... + P m ( z ) , (1)

где P_l ( z ) – локальное кольцо полиномов, образованное неприводимым полиномом p_l ( z ) над полем GF ( p ); l = 1; 2 … m .

В этом случае вычисления модулярном полиномиальном коде (МПК) организуются параллельно, помодульно и независимо друг от друга, так как операции сложения, вычитания и умножения сводятся к соответствующим операциям над остатками по модулям p _l( z ) над полем

I A( z) ® B( z )|+p( z) = a( z) ® Д( z)| + (z) , (2)

где ⊗ – операции сложения, вычитания и умножения в GF(p ); A(z) = ( a 1 (z), a 2 (z),..., a _n ( z ) ) и B ( z) = ( в 1 ( z ), в 2 ( z ),---, в n ( z ) ) — модулярный кодвкольцеполиномов; a l (z) = A( z) mod p_t (z) ; в l (z) = B(z) mod p_t (z) ; l = 1; 2 . „ m.

Применение обобщенного ДПФ в кольце полиномов для вычисления d спектральных составляющих возможно, если существует преобразования над конечным кольцом P_l ( z )

d-1

X * (z■) = Z x n (z') A" ( z ) , (3) n = 0

где { X i^k ( z ), х П ( z ), в?ⁿ ( z ) } e P i ( z ) , l = 1; 2 … m; k = 0; 1 … d – 1.

Качественный скачок в повышении скорости реализации задач ЦОС может быть достигнут за счет применения параллельно-конвейерных методов вычислений. Среди таких методов обработки данных наиболее оптимальными для микроэлектронной реализации считаются систолические методы. Эти методы ориентированы на параллельно-конвейерное выполнение наиболее трудоемких вычислительных операций и позволяют эффективным образом реализовать широкий класс алгоритмов ЦОС путем обеспечения предельной для данного уровня технологии производительности вычислительных средств.

Систолические структуры представляют собой множество идентичных функциональных модулей процессорных элементов (ПЭ), соединенных между собой посредством локальных связей. При этом каждый ПЭ соединен только с ближайшими соседними ПЭ для передачи данных. Основным принципом систолической системы является то, что все данные регулярно и ритмически проходящие через массив ПЭ используются многократно. Это позволяет значительно повысить эффективность СП ЦОС и достичь высокой вычислительной производительности за счет распараллеливания вычислений, сокращения времени обмена данными и совмещении процедур ввода, вывода и получения промежуточных результатов.

Математические модели систолических ортогональных преобразований сигналов обладают основными свойствами [6]:

• -    модель может быть описана с помощью небольшого количества типов операторов;

• -    систолические алгоритмы позволяют широко использовать мультиобработку и конвейерные методы;

• -    потоки данных и управляющие связи между операторами являются простыми и регулярными, чтобы ПЭ могли быть объединены в сеть с локальными регулярными межсоединениями.

В настоящее время известно большое количество систолических математических моделей и вычислительных структур для решения самых разнообразных задач цифровой обработки сигналов [6]. Наибольшее распространение в спецпроцессорах, реализующих ортогональные преобразования сигналов в реальном масштабе времени, получили систолические матрицы с линейным типом связи между процессорными элементами. Наиболее простыми по структуре и обладающими максимальным быстродействием являются многоканальные систолические матрицы (МСМ) с блоком регистров-накопителей.

Рассмотрим структуру и функционирование таких матриц. Как правило, систолические алгоритмы обобщенного ДПФ записываются в виде рекурсивных выражений, например по схеме Горнера

X(k) = (((x,(d - 1)вk + x,(d -2))ei ++ ... + xi(1))eik + xi (OX)mod p; (z) (4)

где β – первообразный элемент мультипликативной группы порядка d , порождаемой полиномом p_i ( z ); k = 0; 1 … d – 1; i = 1; 2 … m ;

xi (n) = x(n) mod pt (z).

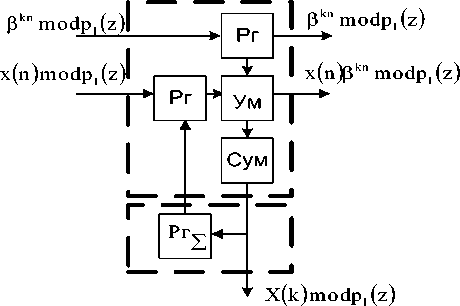
Рис. 1. Структура процессорного элемента

Однофункциональная МСМ содержит d однотипных процессорных элементов, структура которых показана на рис. 1. В состав ПЭ входят два регистра Рг, предназначенные для хранения чисел разрядностью ord p_i ( z ), умножитель У и сумматор ∑ по модулю p_i ( z ), а также регистр-накопитель Рг_∑, предназначенный для хранения промежуточных результатов. Каждый j -й ( j = 1; 2 … d ) ПЭ МСМ реализует процедуру (4) согласно равенству

X i (j, n) = X i (j, (n — 1)) + X (n — j ) в ^ j ⁾⁽ j ^{- 1)} , (5 где n – текущий такт вычислений, причем j <  n <  d + j - 1 ; X i ( j , n ) - значение накопленной суммы в n -й такт в j -м регистре-накопителе РГ_£; X i ⁽ j,^{(n -} 1)) – то же на ( n – 1)-м такте; x i ( n — j ) - значение обрабатываемого отсчета исходных данных на n -м такте в j -м про- ( n - j )( j - 1) цессорном элементе по модулю p_i(z); β _i – значение поворачивающего коэффициента, поступающего на вход j -го ПЭ модуля p_i ( z ) в n -й такт.

Как видно из (5), вычисления X i ( j , n ) осуществляются в независимых ячейках МСМ за счет разделения групп операций умножения и сложения по модулю p_i ( z ). Это обеспечивает более высокую производительность вычислений спецпроцессору ЦОС. На рис. 2 представлена структура систолической матрицы ЦОС, реализующей обобщенное ДПФ в кольце полиномов 65432

• P ( z) = z + z + z + z + z + z + 1.

Данное кольцо задается двумя неприводимыми полиномами p1 (z) = z 3 + z 2 + 1 и p2 (z) = z3 + z + 1. Каждый из полиномов порождает мультипликативную группу, содержащую семь ненулевых элементов. В данных группах в качестве порождающего элемента вi (i = 1; 2) выбран z. Таким образом, в данном кольце реализуется ортогональное преобразование аналогич- ное ДПФ с обработкой входного окна, состоящего из d = 7 отсчетов.

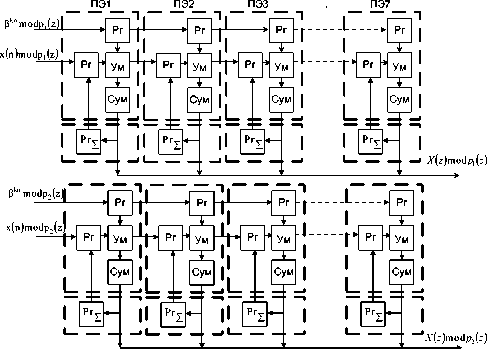
Рис. 2. Многоканальная систолическая матрица обобщенного ДПФ в кольце полиномов

На рис. 3 приведена временная диаграмма работы систолической матрицы обобщенного ДФП типа МСМ. Перед началом работы матрицы содержимое всех регистров Рг∑ равно нулю.

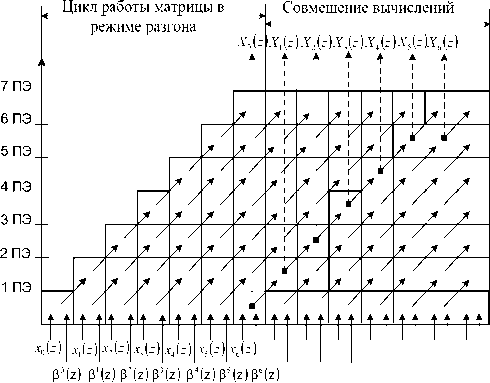
Рис. 3. Диаграмма работы систолической матрицы

На первом такте работы в первый ПЭ поступают значения xi (0T) = x(0T) mod Pj (z) и вi0 . Через время τ1 + τ2, где τ1 – время приема-передачи данных, τ2 – время выполнения операции умножения, производится суммирование xi(0T) с содержимым Рг∑. На такте τ4 осуществляется запись полученной суммы в регистр Рг∑. На втором такте работы МСМ значение xi(0T) и β i0 передаются из первого ПЭ во второй и одновременно в первый ПЭ поступают новые значения xi(1T) и β i1 . На такте τ2 второго такта работы значение первого отсчета xi(1T) задерживается в элемен- те задержки, а во втором ПЭ xi(0T) умножается на поворачивающий коэффициент βi0 . Далее на такте τ3 в обоих ПЭ выполняется суммирование, а результаты этой операции записываются в соответствующие регистры Рг∑.

Таким образом, начиная со второго такта, первый и второй ПЭ работают синхронно. На d -м такте параллельно работают все ПЭ, а в конце d -го такта результат выполненного в первом ПЭ передается на общий выход блока регистра-накопителя. На ( d + 1)-м такте окончательный результат будет сформирован во втором ПЭ МСМ, на ( d + 2)-м – в третьем ПЭ и т.д. Если на ( d +1)-м такте вводятся новые значения отсчетов, то в МСМ одновременно будут обрабатываться два вектора данных. В установившемся режиме вычислительный процесс реализуется за время

Т = Т , + Т + Т ,   .

сист      псс - мод     мсм мод-псс ^,

где Тпсс-мод – время выполнения прямого преобразования из позиционного кода в модулярный код; Тмсм – время работы систолического конвейера; Т – время обратного преобразования из мо-мод-псс дулярного кода в позиционный.

Очевидно, что для обеспечения эффективной работы вычислительного конвейера необходимо, чтобы модули прямого и обратного преобразований работали синхронно с систолической матрицей. В работе [4] представлены структуры и алгоритмы работы таких устройств, позволяющих согласовать скорость МСМ с скоростью выполнения данных немодульных операций.

Применение модулярного полиномиального кода позволяет не только повысить скорость обработки данных, но и обеспечить отказоустойчивость СП ЦОС [4; 7-8]. Если из набора n неприводимых полиномов выбрать k информационных многочленов ( k < n ), позволяющих обеспечить требуемую точность вычислений, то это позволит определить величину рабочего диапазона k

Рраб (z) = П Pt(z), входящего в состав полного i =1 n диапазона Рполн = П Pi (z) • Тогда многочлен i=1

A ( z ) с коэффициентами из поля GF ( р ) будет считаться разрешенным, в том и только том случае, если A ( z ) е Р _раб ( z ) . Следовательно, местоположение A ( z ) относительно Р_раб ( z ) позволяет однозначно определить, содержит ли модулярный код ошибочные символы или нет.

Для реализации эффективной борьбы с последствиями ошибок, вызванных отказами в вычислительных трактах СП, необходимо опреде- лить минимальную избыточность модулярного кода. Рассмотрим теорему оценки корректирующих способностей кода класса вычетов с двумя контрольными основаниями.

Теорема 1. Если в упорядоченном избыточном полиномиальном модулярном коде, для которого справедливо ord pi(z)< ord p2(z) < ... < ord pk(z)

для двух контрольных оснований pk+1(z) и pk+2(z) имеет место соотношение ordpk+i(z)+ ordpk+2(z) > ordpk(z)+ ordpk_ i(z), (7) то они позволяют определить местоположение и величину однократной ошибки по любому основанию.

Доказательство. Пусть A ( z ) = ( a ₁( z ) … a_k ( z ), a_k+1 ( z ), a_k+2 ( z )) принадлежит рабочему диапазону A ( z ) ∈ P_раб ( z ). Произведем искажение остатков по двум различным основаниям p ( z ) и p . ( z ), где i * j. Тогда коды

A-(z) = (a i ( z ) ... a ,* ( z ), a j z ) ... a k+i ( z ), a k+2 ( z )),

A j* (z) = (a i ( z ) ... a,{ z ), a/( z ) ... a k+i ( z ), a k+2 ( z ))

будут отличаться от исходной комбинации A ( z ) по одному модулю a. *( z ) * a . ( z ) и a j *( z ) * a j ( z ).

Тогда для однозначного определения величины ошибки и ее местоположения необходимо, чтобы интервалы диапазонов, в которые попадают ошибочные полиномы Ai (z) и Aj (z), не совпадали, то есть li(z) * lj(z), где li(z) = [|A(z) + Aai(z)Bi(z)|+Pполн /Рраб(г)];

l j (z) = [| A ( z ) + Aa_/( z ) B _/. ( z )| ⁺Pполн / P^z )]; * Aa i (z)= a i (z) - a *i ( z ); Aa j (z)= a j (z) - a *j ( z ).

Положим, что A ( z ) = 0, а i = k – 1, j = k . Тогда условие однозначного обнаружения и коррекции ошибки примет вид

[ A + Aa k-1 ( z ) B k-1 ( z )| ⁺pполн / P pa6 ( z )|] -

• -    [| A + Aa k ( z ) B k ( z )| ⁺Pполн / P pa6^ z )|] > 1,     ⁽⁸⁾

отсюда следует

|Aa k-1 ( z ) B k-1 ( z )| ⁺Pполн - |Aa k ( z ) B k ( z )| ⁺Pполн ≥ P pa6 ( z ). (9)

Сократим обе части неравенства (9) на P_раб ( z ). Получаем

|Aa k—i ( z ) B k—i ( z )/ P pa6 ( z )| ⁺Рполн

• -    |Aa k ( z ) B k ( z )/ P pa6 ( z )| ⁺Рполн > 1-

• Исходя из Pполн(z) = Pраб(z) pk+1(z) pk+2(z) и определения ортогональных базисов Bi(z), имеем

Pk +1 ⁽ z ) P k +2 ⁽ z ) ( ( ^{A a} k -1 ⁽ z ) m k-1 ⁽ zV P k -1 ⁽ z ) ) — ,

— ⁽ A ^a k ⁽ z ) m k ⁽ z )/ p_k ⁽ z ) )) mod ^р конт ⁽ z ) > 1 ’ ⁽ 0 где P KOHT = P k + 1 ( ^{z )} P k + 2 ( ^z ) . Приведя к общему знаменателю, получаем, что числитель дроби удовлетворяет условию

А ^а k _ , ⁽z ) m k - j ⁽z ) P k ⁽z ) ^- A ^a k ⁽z ) m k ⁽z ) p k - , ⁽z )

-

+

> 1 , (11)

Р пол ( z )

и тогда pk+i(z) pk+2(z)/(pk-i(z) pk(z)) > 1-Переходя к порядкам полиномов, имеем ordpk+i(z)+ ordpk+2(z) > ordpk—i(z) + ord^k(z), что и требовалось доказать.

Применение данной теоремы позволяет разработать алгоритмы и методы поиска и коррекции ошибок в МПК, обеспечивающих требуемый уровень отказоустойчивости при минимальной избыточности.

Анализ известных методов контроля и коррекции ошибки в модульных избыточных кодах показал, что данные процедуры базируются на вычислениях позиционных характеристик кодов МПК, среди которых особое место занимает интервальный номер [4].

Поскольку ошибка переводит A ( z ) = (a i ( z )... a k ( z ),a k + i ( z ),a k + 2 ( z )) в ошибочный полином A * ( z ) , лежащий вне рабочего диапазона, то, зная номер интервала, куда попал искаженный полином A * ( z ) , можно определить основание, по которому произошла ошибка, а также ее глубину.

Процесс определения данной характеристики осуществляется согласно выражению

1инт (z) = [ A(z)/Рраб (z)].         (12)

Несмотря на то, что процедура (12) относится к немодульным, ее сводят к совокупности модульных операций. В [4] представлено устройство, осуществляющее обнаружение и коррекцию ошибки в модулярном полиномиальном коде на основе вычисления интервального номера. Применение свойства подобия ортогональных базисов полной, содержащей контрольные основания, и безызбыточной системы МПК позволило уменьшить схемные затраты на реализацию устройства обнаружения и коррекции ошибок [8].

Для обеспечения меньших временных затрат на процедуры вычисления интервального номера полинома целесообразно использовать связь данной позиционной характеристики с нормированным следом. Нормированный след полинома получается в результате операции вычитания из модулярного кода псевдоортогональных базисов, у которых ортогональность нарушена по контрольным основаниям. В этом случае справедлива следующая теорема.

Теорема 2. Если в упорядоченной системе МПК, содержащей k информационных и r избыточных оснований, в результате получен нормированный след полинома

(0,0,0, „ . ,0, Y k + 1 ⁽ z ), Y k + 2 ⁽ z ),-, Y k + r ⁽ z )) , (13) то номер интервала, в который попадет ошибочный полином A * (z) , определяется по формуле

+

l ( z ) = инт

k + r

E Rj(z)Yj(z)

j = k + 1

конт

k+r где Rj (z) = [Вj (z)/Рраб (z)J; Рконт = П P^z) ■ i=k+1

Доказательство. Докажем вначале, что если хотя бы один yj (z) ^ 0 , где j = k + 1 — k + r, то полином A (z) является запрещенным. Заменим произведение r избыточных оснований МПК од-k+r ним составным основанием Тогда полином

Р конт = П P.^{( z )} ■ i = k +1

^A( z ) = fa ( z ), « 2 ( z )- « k + 1 ^{( z)} - « k + r ^{( z ))}, представленный в виде ( k + r )-мерного вектора, примет вид

A(z) = (ai (z) a2 (z) - ak (z),aконт (z)) , (15)

где A ⁽ z) = ^a конт ⁽ z )mod ^P K_OHm ⁽ z).

Тогда, согласно определению нормированного следа, если в кодовой комбинации A ( z ) произошла ошибка, то результатом операции параллельной нулевизации A ( z ) с использованием псевдо-ортогональных базисов будет отличный от нуля нормированный след

(0,0,0...0,Y конт ( z)),            (16)

где   Y _тн» = и/ .. L z ) - E у ^(z^modP^z);

Y Конт ^{( z )} = B * ⁽ z)mod ^р конт ⁽ z ) ; B * ⁽ z ) ^- ортого нальный базис безызбыточной системы МПК.

С другой стороны, согласно КТО

Yконт (z) = E YКонт(z)Uj (z)modрконт (z), (17) j=k+1

где Y kKoht ( ^{z )} ^ Y ( z )mod p j ⁽ z ) ; U j ( z ) - ортогональный базис МПК с основаниями p_k+1 ( z ) …

^Bk+ _r ( z ). Так как Y _конт (z) ^ 0 , то хотя бы один Y Конт ( z ) отличен от нуля.

Таким образом, если в результате параллельной нулевизации A ( z ) и псевдоорто-гональных базисов получен след полинома (0, ^ 0, y k + i ( ^{z )} ... Y_{k + r} ( z )) ^ 0 , то данный полином содержит ошибку.

Докажем теперь, что величина интервального номера l ( z ) полинома A ( z ) определяется выражением (14).

Пусть в результате процедуры нулевизации полинома A ( z ) получим нормированный след

Y(z) = (0,0,0... 0,yk+i(z),Yk+2(z) ... Yk+r(z)), отличный от нуля. Известно, что

A* (z) = A( z) + ^A; (z),         (18)где        AAi (z) = (Aai (z)B(z))modрпОЛн (z) ;

A a i ( z ) - глубина ошибки по i -му основанию.

При этом

AA. (z) = y (z) = (0,0...0, /k+i (z)yk+2 (z)... Yk^r (z)) ■

Тогда на основании (18) имеем

1инт (z) = [a* (z)/ Рраб (z )] == [a( z ) + M(z >/ Рраб ( z )] = [Y( z V Рр.б (z)] .(19>

Согласно КТО и с учетом ai (z) = 0, i = 1; 2... k, имеем k + r

Y(z) = ( E Yj (z)Bj (z)) mod рполи (z) ■ (20) j=k+1

Подставляем (20) в равенство (19), получаем luHT ( z )

k +r                   /

= E YAz>B,(z) /РрабСz)

_j=k +1                /

Учитывая подобие ортогональных базисов и делимость без остатка ортогональных базисов контрольных оснований на рабочий диапазон, имеем

+

l uHT ( ^{z )}

k + r

E Rj(z)Yj(z))

j = k + 1

^Р кат ⁽ z )

где R j . ( ^{z )} = ^[ b j ( z ) ^Р раб ( ^{z ) ]} ■

В таблице 1 представлены схемные и временные затраты, необходимые при вычисления интервального номера для различных алгоритмов процессоров МПК, функциони- рующих в расширенных полях Галуа GF(23), GF(24), GF(25).

Таблица 1. Затраты на вычисление интервального номера

№ п/п	Алгоритм	Затраты
		аппаратурные (нейроны)			итерации
		GF(2 3 )	GF(2 4 )	GF(2 5 )
1	[4]	17	52	139	2
2	[8]	14	47	130	2
3	теорема 2	14	44	115	1

Анализ таблицы 2 показывает, что оптимальным способом реализации немодульной процедуры определения, локализации и исправления ошибки для конвейерной структуры процессоров МПК с двумя контрольными основаниями, удовлетворяющим предельной теореме 1, является метод, доказанный в теореме 2. Данный метод реализуется при этом минимальных аппаратурных и временных затрат. Для оценки отказоустойчивости непозиционного СП ЦОС, функционирующего в кольце полиномов, произведем сравнительный анализ со СП БПФ. Спецпроцессоры предназначены для обработки 20 разрядных данных. Полученные результаты исследований представлены в виде зависимостей на рис. 4, где для удобства воспользуемся обозначениями: 1 – вероятность безотказной работы отказоустойчивого непозиционного СП ЦОС; 2 – вероятность безотказной работы СП БПФ.

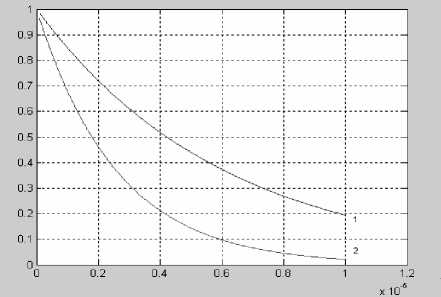
Рис. 4. Сравнительная оценка надежности функционирования СП ЦОС

Анализ зависимостей позволяет сделать вывод о том, что применение модулярного полиномиального кода позволяет более чем 1,9

раза повысить надежность функционирования по сравнению с аналогичным СП БПФ с троированной мажоритарной структурой. При этом временные затраты на реализацию обобщенного ДПФ в кольце полиномов с использованием систолической модели обработки сигналов снижены в 1,4 раза по сравнению с быстрым алгоритмом дискретного преобразования Фурье по основанию два. Полученные данные свидетельствуют о целесообразности использования параллельно-конвейерных методов реализации ортогональных преобразований сигналов в перспективных инфокоммуникаци-онных технологиях.