Высокотемпературные фазовые равновесия и термодинамические свойства расплавов в системе CaO-Si02

Система CaO-SiO2 является основой для подавляющего числа шлаков черной и цветной металлургии, цементов, огнеупоров и ряда других важных материалов. Несмотря на практическую значимость этой системы, информация о строении ее фазовой диаграммы и термодинамических свойствах фаз до настоящего времени остается недостаточно полной.

Ориентировочные представления о фазовых равновесиях в системе CaO-SiO2 были описаны в 1903 году Фостом. Первое относительно подробное исследование диаграммы состояния выполнено Дэем, Шефердом и Райтом в 1906 году. Внесение исправлений и исследование отдельных деталей диаграммы производилось в работах Шеферда, Ранкина и Райта (1911-1915 г.), Грейга (1927 г.), Карлсона (1931 г.), Ли и Дема (1935 г.), Эйтеля (1938 г.), Колобовой (1941 г.), Муана и Осборна (1951 г.), Ольшанского (1952 г.), Делла и Роя (1958 г.), Уэлча и Гатта (1951 г.) и др. исследователей [1,2, 9].

К настоящему времени в системе CaO-SiO2 идентифицировано наличие четырех сложных химических соединений: CaOSiO2, 3CaOSiO2, 2CaOSiO2, 3CaOSiO2. Для некоторых из них температурные области существования и характеристики плавления недостаточно ясны [2, 9].

Материалы исследований фазовых равновесий в системе CaO-SiO2 подробно рассмотрены и обсуждены в работах [1, 2]. На рис. 1 показан обобщенный вид диаграммы состояния системы CaO-SiO2 по данным справочников [1, 2]. Пунктирными линиями на диаграмме изображены линии фазовых равновесий ход которых недостаточно ясен или вызывает сомнения. Из рисунка следует, что наиболее надежными являются сведения о фазовых равновесиях: «SiOr-расплав», «CaOSiO2, (псевдоволластонит) - расплав», «3CaOSiO2 (ранкинит)-расплав», «2СаО8Юг-расплав». Практически неисследованными являются фазовые равновесия «СаО-расплав», «ЗСаОБЮг-расплав».

Область существования в системе жидкой фазы исследована недостаточно полно. Известно, что при температуре порядка 1700 Св интервале концентраций SiO2 от 72 до 99 мае. % в системе наблюдается расслоение жидкой фазы на две несме-шивающиеся жидкости. Экспериментальное исследование этой области системы проводилось в работах Грейга [4] и Ольшанского [3]. Результаты указанных исследований отражены на рис. 2. Приведенные данные констатируют наличие на диа грамме состояния системы области расслаивания, но не позволяют с необходимой точностью отразить ход линии расслоения.

Термодинамические свойства расплавов исследованы в незначительной степени. Зависимости активностей компонентов от состава расплава экспериментально изучались Картером и Макфарлай-ном [6], Бэрдом и Тейлором [7]. Построенные по результатам этих исследований концентрационные зависимости считаются достаточно надежными и приводятся в справочнике [5].

Рис. 1. Диаграмма состояния системы CaO-SiO2 по данным [1, 2]

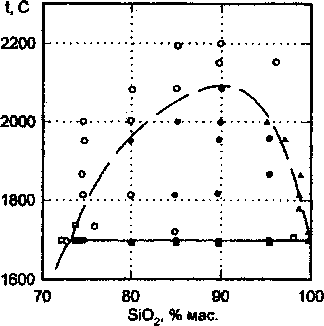
Рис. 2. Область расслаивания жидкой фазы по данным Грейга и Ольшанского

Цели настоящей работы состояли: 1) в проведении комплексного термодинамического анализа высокотемпературных фазовых равновесий в системе CaO-Si02 с использованием сведений о термодинамических характеристиках сложных химических соединений; 2) в получении на основе согласованных термодинамических данных расчетной фазовой диаграммы системы; 3) в определении основных термодинамических характеристик расплавов CaO-SiO2 на основе полученных в ходе термодинамического анализа модельных уравнений.

Анализ равновесий «расплав-твердая фаза» в системе СаСГ-8Ю2 возможен на основе рассмотрения следующих химических реакций:

1 (СаО) = СаО тв.;(1)

3 (СаО) + (SiO2) =ЗСаО- SiO2 тв.;'(2)

2 (СаО) + (SiO2) =2СаО- SiO2 тв.; (3) 3 (СаО) + 2 (SiO2) =2СаО- SiO2 тв.; (4)

(СаО) + (SiO2) =СаО-SiO2 тв.; (5)

(SiO2) = SiO2 тв.(6)

В обобщенном виде эти реакции можно выразить уравнением т ■ (СаО)+и • (SiO2) = тСаО ■ nSiO™. (7)

в котором, т и п являются стехиометрическими коэффициентами, показывающими числа молекул простых оксидов, входящих в молекулу твердой фазы.

Условием равновесия реакции (7) является соотношение тР1 1 + nMai = ^mCaO-nSiO^ >         (8)

в котором цп - химический потенциал СаО в расплаве, - химический потенциал SiO2 в расплаве, ЦтСа0 п5юг ~ химический потенциал чистого твердого химического соединения mCaOnSiO2 .

В соответствии с обобщенной термодинамической моделью жидкого шлака [8] термодинамические характеристики расплава системы CaO-SiO2

характеризуются следующими зависимостями.

УУрутщ к?4      >

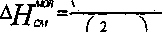
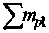
AST

Г2        >

-->Л %[«12 +Аг(2п ~4>01 -^)]-

-R-^x, ln(x,)

Ai = A°i + ^vn ■-R71n(x₁) + v₁*₁ -^ (5₁₂ -7a₁₂)- -[^(^ -'2x₁)+2x_tx₂(x₁ -хД^ -z₂₁)-(^2 -%)} -(H)

Ai ~Z^i + ^v2i •7?71n(x₂)+v₂₁ -{x² -(6i2 ~7a₁₂)— -[xA -2x₂)+2x_lx₂(x₂ -^^{z^ -z₂₁)-(712 “^Аг)} (¹²)

Здесь ^Hc.™ , ^S™ ~ молярная энтальпия и молярная энтропия образования расплава из жидких оксидов; Д], р₂₁, Д, /41 ^- химические потенциалы оксидов в расплаве и химические потенциалы чистых жидких оксидов; Уц, v₂₁ - числа катионов в молекулах СаО и SiO₂, соответственно; т_р1 - числа молей различных сортов оксидов в расплаве; z£_t, z₂₁ - координационные числа катионов в чистых жидких оксидах; Xj, х₂ - ионные доли катионов кальция и кремния в расплаве; 5₁₂, Аз ^{и а}12’ Р\г ~ энтальпийные и энтропийные параметры модели; 7 - температура расплава.

После подстановки выражений (11) и (12) в соотношение (8) и проведения несложных преобразований, условие равновесия реакции (7) запишем в виде

А ¹612 ⁺ А • “12 ⁺ А ¹712 ^{+ а}4 ■ Аг = ^Y •   (13)

В уравнении (13) параметрами а_г, а₂, а₃, а₄, Аг, ^Y являются величины, определяемые уравнениями:

^ =ш-х₂+и-х² , а₂ =-а₁-Т,

Оз = -т [х₂ (х₂ - 2x_t) +2x^₂ (xj - х₂)]+

+И [Xj (х, - 2X2 ) +. 2XjX₂ (х₂ - x_t)],

А ⁼ ~^аз Т - 71'г ⁼ 712(^zii ~^z2i) > Аг ⁼Аг(²и ~^z2i)>

Y = bG^°-RT OTln(xj)-«ln(x₂) .

Входящая в последнее уравнение величина AG° характеризует стандартное изменение энергии Гиббса для реакции образования твердой фазы из жидких простых оксидов.

т ■ СаО^ж+п ■ SiOi = тСаО • nSiO^ . (14)

Численные значения AG® для конкретных температур могут быть рассчитаны на основе справочных данных, характеризующих термодинамические свойства участников реакции (14).

Полученное в общем виде уравнение равновесия «твердая фаза-расплав» (13) позволяет решать две важные задачи. Первую - определять на основе экспериментальных данных, о строение высокотемпературной области диаграммы состояния и справочных данных о температурных функциях AG° численные значения параметров модели оксидного расплава, а следовательно, выявлять таким образом термодинамические характеристики жидкой фазы. Вторую - на основе известных термодинамических характеристик твердых и жидких фаз рассчитывать координаты точек линий фазо- вых равновесий на диаграмме состояния исследуемой системы, определяя их наиболее вероятный ход.

В математической формулировке первая задача при известных температурных функциях AG° сводится к формированию и решению переопределенной системы линейных уравнений в которой известными параметрами являются координаты точек на линиях фазовых равновесий, а неизвестными - параметры термодинамической модели. Вторая задача при заданных температурах и известных термодинамических параметрах твердых и жидких фаз представляет собой решение конкретных уравнений фазовых равновесий относительно неизвестного параметра - концентрационной координаты точки на линии рассматриваемого фазового равновесия.

Последовательное решение указанных задач представляется весьма плодотворным и практически значимым. Решение первой задачи на основе совместного использования разнородных, непосредственно не связанных друг с другом экспериментальных данных, полученных различными методами и с различными целями, делает процесс комплексного моделирования более объективным. В силу практической направленности эту задачу можно рассматривать как разновидность косвенного метода исследования термодинамических характеристик оксидных расплавов. Последующее решение второй задачи позволяет расчетным путем получить внутренне согласованную равновесную фазовую диаграмму исследуемой системы надежность, которой (с учетом сложностей проведения высокотемпературных исследований) может превосходить надежность экспериментальной диаграммы.

В данной работе в качестве экспериментальной основы при проведении комплексного моделирования высокотемпературных фазовых равновесий использовались координаты точек наиболее изученных линий фазовых равновесий «расплав -SiO2», «расплав- CaOSiO2», «расплав - ЗСаО-2SiO2», «расплав - 2CaOSiO2», изображенных четкими линиями на обобщенной фазовой диаграмме системы, приведенной в справочниках [1, 2] (см. рис. 1).

Термодинамические характеристики твердых фаз, способных находиться в исследуемой системе в равновесии с расплавом, в фрагментарном виде содержатся в справочниках [2-5, 10-17], сводка данных из них приведена в таблице. При получении уравнений температурных зависимостей AG° для реакций образования твердых фаз из жидких оксидов в данной работе использовались характеристики, выделенные в таблице курсивным шрифтом. Эти характеристики близки к данным из указанных литературных источников и являются полностью согласованными друг с другом. Выделенные термодинамические значения были установ лены ранее в результате физико-химического моделирования термодинамических характеристик широкого круга веществ, являющихся компонентами твердых металлургических шлаков.

На основе указанных выше данных в соответствие с рассмотренной методикой был проведен расчет параметров термодинамической модели расплава CaO-SiO₂, Ввиду отсутствия надежных данных о термодинамических характеристиках высокотемпературной модификации соединения 2CaO SiO₂ при моделировании фазовых равновесий была выполнена также оценка значений параметров А и В, передающих температурную зависимость

^=А + В-^—       (15)

1         1000

реакции образования этого соединения из жидких оксидов. Расчетные значения всех названных параметров приведены ниже.

2;2 = -249,0 +1,1 кДж/ моль;

^'2 = -331,46 ± 2,8 кДж/ моль;

а12 = -26,71 ± 0,6 Дж/моль град;

Д]'2 = -95,55 ± 1,6 Дж/моль град;

А = -217,98±1,1 кДж/моль;

В = 41,96±0,3 Дж/моль град.

Проверка пригодности теоретических соотношений (9)—(12) с найденными значениями параметров g12, ^12, «12, Д2 ДО» расчета фазовых равновесий и описания термодинамических характеристик расплава проводилась путем сопоставления результатов расчета с имеющимися экспериментальными данными. На основании расчетных координат точек линий фазовых равновесий построена диаграмма состояния системы, показанная на рис. 3. На рис. 4 изображены расчетные зависимости активностей компонентов от состава расплава при температурах 1500 ° С (1773 К) и 1550 ° С (1823 К). На этом же рисунке показаны результаты экспериментальных определений активностей компонентов при соответствующих температурах, полученные в исследованиях Картера и Макфарлайна [6], Бэрда и Тейлора [7]. Сопоставления расчетной фазовой диаграммы с экспериментальной диаграммой (рис. 1), а также расчетных и экспериментальных данных, отображенных на рис. 4, позволяют сделать вывод о том, что результаты расчетов практически совпадают с экспериментальными результатами. Это дает основание полагать, что модельные термодинамические соотношения с достаточной степенью достоверности отражают свойства исследуемой системы.

Теоретические соотношения (9)—(12) с найденными в работе значениями параметров модели 612 , 912, ^а12> Рхг дают возможность рассчитать концентрационные и температурные зависимости основных термодинамических характеристик расплавов системы CaO-SiO₂ определение которых, экспериментальным путем представляется крайне

Вестник ЮУрГУ, № 10,2005

Таблица

Термодинамические характеристики твердых фаз системы CaO-SiO2

Вещества	- AH2gg, кДж /моль	° 298 ’ Дж /моль К	Ср=а + b-Т + с / Т2 Дж/мольК			Температ. интервал, град К	Ист.	Ср расплава, Дж/мольК	Тпл, град К	А Нщ» кДж / моль
			а	b 103	с 10~5
СаО
	635,51 [16]	41,45 [16]	49,65	4,52	-6,95	298-2888	[16]	62,8 [16]	2888(16]	79,5 [16]
	635,54(11,12]	41,74(11,12]	48,86	4,52	6,53	298-2000	[И,2]		2873 [11]	50,24 [11]
	635,59 [2]	41,66 [5]						—	2873 [5]	79,55 (5]
	634,75 [17]	39,78 [17]	49,66	4,52	-6,95	288-1177	[17]	—	2888(17]	79,55(17,12]
	635,09(10]	38,074 [10]						—	2900(10]	52,3(10]
	635,120	41,585	49,180	4,436	—6,694	298-Тпл		61,25	2888	79,48
3CaO-2SiO2 (ранкинит)
	3963,6 [16]	210,93 [16]	267,96	37,89	-69,5	—	[16]	—	Разл.
	3959,27 [12, 17]	211,02(12]						—	Разл.
	3959,1 [И]	211,02 [11]	267,96	37,89	-65,5	298-1000	[И]		Разл.
	3959,2 [2]	211,02 [2]	(267,96)	(37,89)	(-65,5)	—	[2]	—	Разл.	—
	3956,31 [19]	210,02(10]						—	Разл.	—
	3959,159	213,341	262,979	40,717	-53,288	298-1746		358,58	Разл.	—
а СаО SiO2 (псевдо-волластонит)
	1629,5 [16]	87,42 [16]	108,23	16,50	-23,656	298-1700	[16]	150,7 [16]	1813 [16]
	1632,76(11]	87,51 [11]	108,23	16,50	-23,656	298-1700	[И,2]	—	1813 [17]
	1629,12 [12]	87,51(12]						—	1813 [12]
	1629,16(2]	87,51 [2]						—	1817(2]
	1627,58 [10]	86,44 [10]							1817(10]
	1631,729	87,097	106,737	18,665	-22,682	298-1817		148,38	1817	—
SiO2 (кристобалит)
	908,87 [16]	42,7 [16]	60,29	8,54	—	523-2000	[2]	85,83 [16]	2001 [16]	7,70 [16]
	908,91 [11]	43,42(11]	60,29	8,54		523-2000	[Н,2]	83,5 [14]	2001 [11]	7,704(11]
	911,93 [17]	41,49 [17]	72,81	1,30	-41,45	523-1995	[17]	86,25 [17]	1995 [17]	10,87(17]
	910,13 [12]	42,707 [12]						_
	911,398	41,873	56,758	15,326	-14,970	298—Тпл.		85,97	2001	7,59

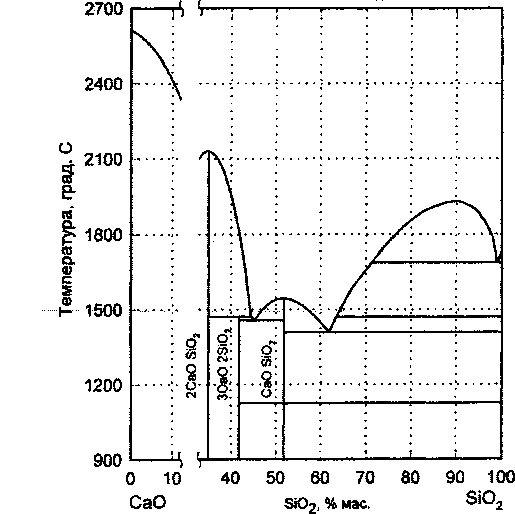
Рис. 3. Расчетная диаграмма состояния системы CaO-SiOz

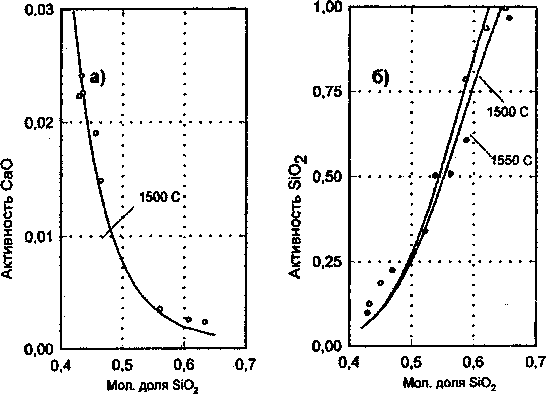
Рис. 4. Расчетные и экспериментальные активности СаО (а) и SiO2 (6) в расплавах системыСаО-ЗЮ2.

Стандартные состояния: СаО - чистый твердый оксид кальция; SiO2 - чистый кристобалит.

о - данные Картера и Макфарлайна; • - данные Бэрда и Тэйлора;

_____-результаты расчета сложным. На рис. 5 и 6 изображены концентрационные зависимости молярной энтальпии и молярной энтропии смешения жидких оксидов от состава образующегося расплава. Ход построенных кривых говорит о том, что процесс образование расплавов с относительно невысокими концентрациями SiO2 сопровождается существенными тепловыми эффектами, что свидетельствует о наличии в расплаве сильных межчастичных взаимодействий. Наличие значительных межчастичных взаимодействий в указанной области составов системы наглядно подтверждается образованием в ней целого ряда сложных химических соединений. По мере дальнейшего увеличения в системе концентрации SiO2 межчастичные взаимодействия в расплаве начинают существенно ослабевать, что приводит в области, богатой SiO2, к распаду расплава на две несмешивающиеся жидкости. Концентрационная зависимость энтропии смещения жидких компонентов качественно согласуется с кривой энтальпии смешения жидких оксидов и свидетельствует о том, что в расплавах рассматриваемой системы имеют место существенные знакопеременные отклонения от кривой, отвечающей

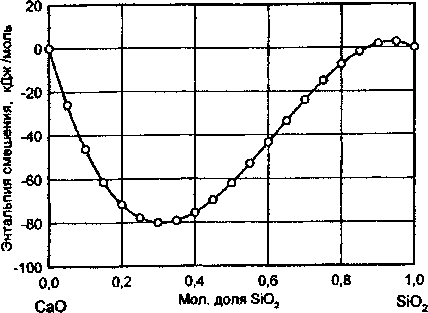
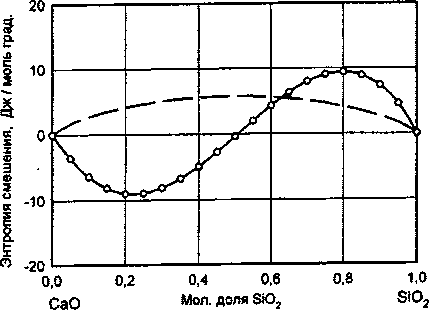
Рис. 5. Концентрационная зависимость энтропии смешения жидких компонентов

Рис. 5. Концентрационная зависимость энтальпии смешения жидких компонентов

модели совершенного ионного раствора (показанной на рис. 6 пунктирной линией).

Выводы

На основе совместного рассмотрения экспериментальных данных о строении высокотемпературной области диаграммы состояния системы CaO-SiO2 и данных о термодинамических свойствах твердых фаз проведен комплексный термодинамический анализ фазовых равновесий и определены параметры термодинамической модели для оксидного расплава исследуемой системы.

С использованием полученного набора термодинамических параметров, характеризующих свойства твердых и жидких фаз, выполнен расчет высокотемпературной области диаграммы состояния системы CaO-SiO2 и зависимостей активностей компонентов оксидного расплава от состава расплава. Сопоставление экспериментальных и расчетных данных свидетельствует о их хорошем согласии.

Определены концентрационные зависимости молярной энтальпии и молярной энтропии смешения жидких оксидов от состава образующегося расплава, согласующиеся с данными о строении фазовой диаграммы.