Высшие гармоники в сетях с дуговыми сталеплавильными печами и их фильтрация

Предложена новая методика определения коэффициента несинусоидаль-ности напряжения в сетях с дуговыми сталеплавильными печами и его нормализация с помощью резонансных фильтров. При этом выбор параметров фильтров и их числа производится в совокупности с соблюдением баланса реактивной мощности. Приводится пример.

В работе [1] дано обоснование нового метода расчета коэффициента несинусоидальности напряжения в сетях с дуговыми сталеплавильными печами (ДСП). В алгоритм расчета введена дзета-функция Римана второго порядка [2]:

/ \   111    7Г

U2)=1^+^+7+-=y> о) что избавило процедуру расчета коэффициента несинусоидальности напряжения от использования громоздких радикалов, как это делается в традиционной методике [3]. Кроме того, такой прием позволяет учесть все гармоники без исключения вплоть до бесконечности, а не до 7-й или 13-й, как это предусмотрено существующей методикой. В результате формула для расчёта коэффициента несинусоидальности напряжения имеет следующий вид:

K = kc-I,                              (2)

где кс - коэффициент схемы кс^Л            (3)

с 1К А

1К - ток короткого замыкания в контролируемой точке, А;

I - ток печной нагрузки, А.

Ток I зависит от числа одновременно работающих ДСП. Так, если в режиме расплавления металла одновременно работает N одинаковых ДСП, то значение тока печной нагрузки будет

I = krIH-^N,                       (4)

где 1н - номинальный ток печного трансформатора, А;

kj = 3,5 - коэффициент кратности тока ДСП, устанавливаемый нормативами ПУЭ [4].

При достижении значения тока 3,5-1Н вступает в работу токовая отсечка регулятора мощности ДСП, и происходит подъем электродов и тем самым -уменьшение тока соответствующей фазы печного трансформатора. Если по какой-то причине токовая отсечка запаздывает, то по селективности должен сработать оперативный печной выключатель, уставка срабатывания которого по рекомендациям ПУЭ [4] настраивается на величину 4 • 1н .

Следует отметить, что существующая методика расчета коэффициента несинусоидальности напряжения принимает в расчет номинальный ток печного трансформатора без учета эксплуатационных коротких замыканий [3], о которых было сказано выше. Это явилось причиной того, что на всех подстанциях, питающих ДСП, как показал опыт их эксплуатации, происходят частые аварии конденсаторных батарей (БК), установленных в компенсирующих установках. Это вполне естественно, так как проектные значения коэффициента несинусоидальности напряжения, полученные по традиционной методике, приблизительно в 4 раза ниже максимально возможных его значений, что доказано как расчетом по новой методике, так и экспериментом [1].

Таким образом, применение дзета-функции Римана существенно упрощает расчет и, кроме того, уточняет результаты расчета примерно на 20 % по сравнению с результатами, полученными по традиционной методике [3]. Решающее значение имеет введение коэффициента кратности тока печной нагрузки к;. В целом, как уже упоминалось выше, максимальное значение коэффициента несинусоидальности напряжения, вычисленное по предложенной методике [1], превосходит приблизительно в 4 раза его значение, найденное по существующей методике [3].

Зачастую уровни высших гармоник в сетях с ДСП выходят за пределы, допустимые стандартом ГОСТ 13109-97. Поэтому актуальной задачей является их нормализация. Если не удается ее осуществить схемными решениями, то необходимо применять фильтрацию. Опыт использования резонансных фильтров показывает, что необходимо устанавливать фильтры подряд, начиная со 2-й гармоники: Ф2, ФЗ и т.д. По теоретическим соображениям четных гармоник быть не должно, однако из-за несим-метрии напряжений и параметров элементов сети по фазам четные гармоники также возникают. В связи с этим при отсутствии четных фильтров могут возникать резонансные явления в системе электроснабжения, при которых обычно выгорает один из нечетных фильтров, что является крупной аварией с большим экономическим ущербом.

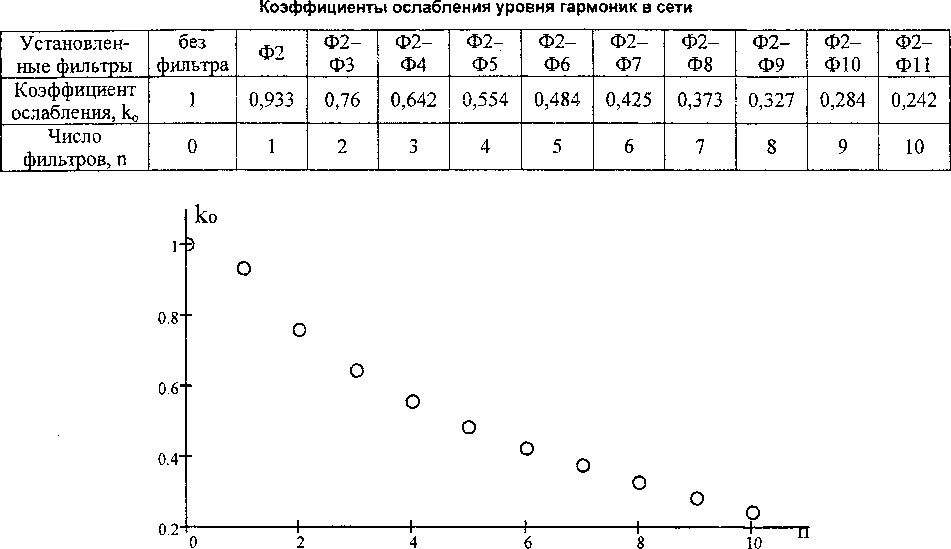
Рис. 1. Зависимость коэффициента ослабления уровня гармоник от количества фильтров

Используя таблицу и кривую на рис. 1, можно определить коэффициент ослабления высших гармоник напряжения к0 в зависимости от установки того или иного числа фильтров п. При этом количество фильтров необходимо выбирать с учетом баланса реактивной мощности. Ток печной нагрузки целесообразно рассматривать в виде случайной величины с нормальным законом распределения [1].

Пример. К одной из секций шин 6 кВ главной понизительной подстанции (ТПП) на машиностроительном заводе подключено три ДСП-5 с печными трансформаторами номинальной мощности S_H = 4 МВ А каждый (рис. 2). Мощность короткого замыкания для этой секции шин составляет S_K= 165 МВ-А [1]. Расчет баланса реактивной мощности показал, что на шинах 6 кВ ГПП необходимо установить компенсирующее устройство мощностью 8,5 Мвар.

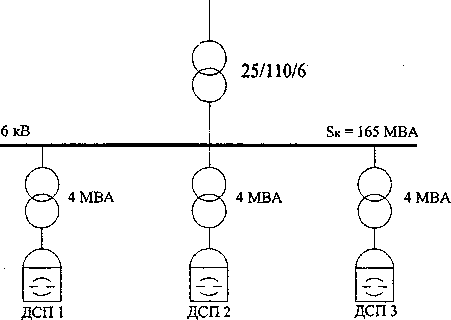
Рис. 2. Исходная схема сети с тремя ДСП

Требуется дать вероятностную оценку коэффициента несинусоидальности напряжения на шинах ГПП, определить количество фильтров, необходимое для возвращения коэффициента несинусоидальности в пределы, устанавливаемые ГОСТ 13109-97, который допускает К < 5 %.

В работе [1] приводятся результаты расчёта для данного примера, полученные обычным способом, без применения компьютерных программ. Ниже (см. рис. 3) демонстрируется процедура анализа уровня высших гармоник с помощью программы в среде Matlab 6.5 Simulink. Данная программа определяет математическое ожидание mk, %, максимальное значение Ктах, %, которые указаны на схеме рис. 3., а также выводит график плотности распределения коэффициента несинусоидальности (рис. 4).

Результаты расчета показывают, что максимальное значение коэффициента несинусоидальности напряжения на шинах 6 кВ ГПП, равное 7,437 %, далеко выходит за пределы стандарта. Для его нормализации принято решение установить на ГПП резонансные фильтры. При этом параметры фильтров и их количество должны выбираться с соблюдением баланса реактивной мощности.

Для выполнения баланса реактивной мощности в СЭС необходимо установить на ГПП компенсирующее устройство мощностью 8,5 Мвар. По каталогу «Информэлектро» 05.82.01-89 выбираются и устанавливаются резонансные фильтры Ф2, ФЗ, Ф4, Ф5. Полная реактивная мощность каждого фильтра составляет 2,7 Мвар. Компенсирующая способность по первой гармонике соответственно равна 2,08 Мвар для фильтров Ф2, ФЗ

Волков Л.Т., Новоселов Н.А.

Высшие гармоники в сетях с дуговыми сталеплавильными печами и их фильтрация

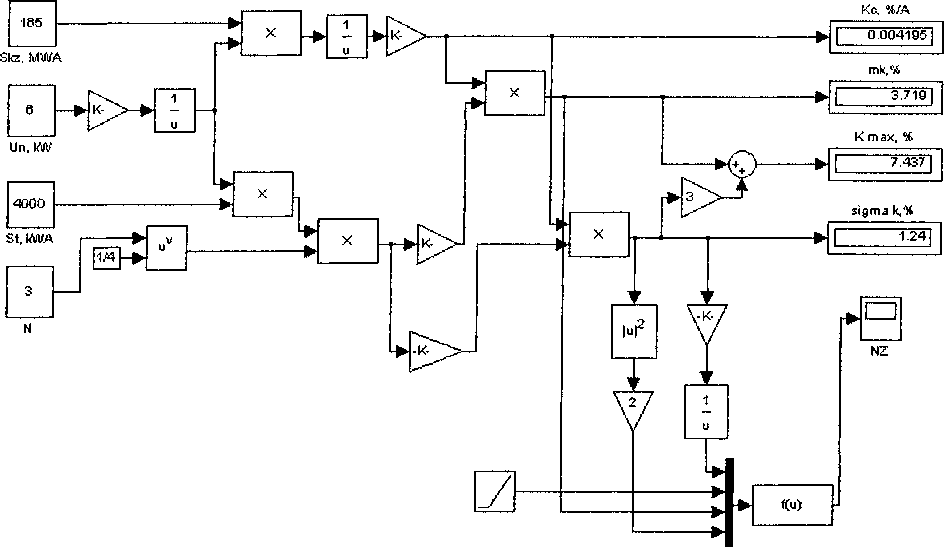
Рис. 3. Схема расчета коэффициента несинусоидальности напряжения в сети с ДСП в среде Matlab 6.5 Simulink

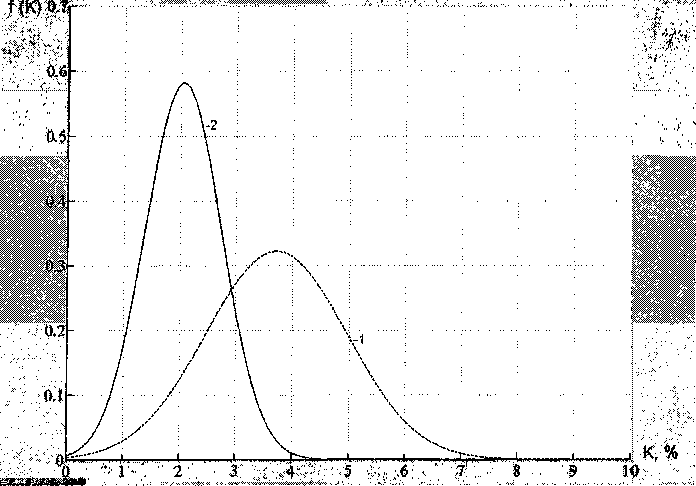
Рис. 4. Плотность распределения коэффициента несинусоидальности напряжения: 1 - без фильтрации; 2 - с фильтрацией

и 1,92 Мвар для фильтров Ф4, Ф5. Таким образом, суммарная компенсирующая способность резонансных фильтров составляет 8 Мвар. Для того чтобы баланс реактивной мощности выполнился полностью, дополнительно устанавливается на шины 6 кВ БК мощностью 0,5 Мвар.

Анализируя результаты расчета, приведенные на рис. 3 и 4, приходим к выводу, что предпринятая фильтрация почти вдвое снижает уровни высших гармоник в питающей сети. Так, если до установки фильтров максимальное значение коэффициента несинусоидальности было равно 7,437 %, то после их установки оно составило

К = 7,437- к0 = 7,437-0,554 = 4,12 %, где к0 = 0,554 - коэффициент ослабления, взятый из таблицы или кривой рис. 1.

Еще более полную картину результатов фильтрации дают кривые распределения коэффициента несинусоидальности напряжения на рис. 4.

25/110/6

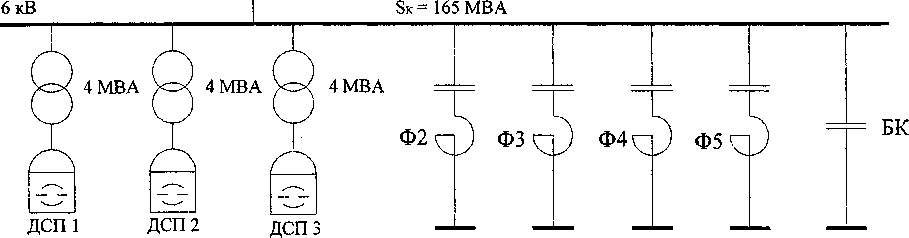
Рис. 5. Итоговая схема сети с тремя ДСП и системой фильтров

Итоговая схема сети с тремя ДСП и системой фильтров показана на рис. 5. Она полностью удовлетворяет требованиям ГОСТ 13109-97 с точки зрения уровня высших гармоник на шинах ГПП и баланса реактивной мощности.

Выводы

• 1.    Использование новой методики и программы расчета в среде Matlab 6.5 Simulink позволяет довольно точно определять ожидаемые значения коэффициента несинусоидальности напряжения в сетях с ДСП.

• 2.    На основании более точного расчета появилась возможность правильно выбирать параметры и количество резонансных фильтров для нормализации коэффициента несинусоидальности напряжения в сетях с ДСП.