Вывод аналитического выражения для разности хода лучей, прошедших интерферометр Жамена

Для экспериментальных исследований наиболее универсальными методами являются методы когерентной оптики, а именно методы голографической интерферометрии. Эти методы позволяют решать такую задачу, как исследование напряженно-деформированного состояния объектов с диффузной поверхностью. Голографическая интерферометрия является высокоинформативным и высокоточным инструментом получения данных. Уникальность методов голографической интерферометрии обусловлена ее возможностями. Эти методы позволяют [1–7]:

– проводить исследования статических и динамических процессов;

– не предъявлять требований к качеству поверхности контролируемых объектов;

– производить сравнение волновых полей, существовавших в различные моменты времени;

– получать информацию об исследуемом процессе как в количественном, так и качественном аспектах;

– воспроизводить трехмерную видеокопию изучаемого объекта.

Со времени первых шагов голографической интерферометрии по внедрению в научную и лабораторную практику большие успехи достигнуты в методике регистрации интерферограмм [1]. Современный уровень развития вычислительной техники и компьютеризация научных исследований позволяют успешно решать задачи третьего этапа — проводить качественный анализ и количественную интерпретацию полученных экспериментальных данных. Однако нет достаточных оснований утверждать, что решены все проблемы в разработке средств и методов оптической обработки голографических интерферограмм.

Изучение существующих подходов к считыванию информации с голографической интерферограммы показал, что наиболее точными и информативными являются фазоизмерительные гетеродинные системы, в которых фазовые характеристики интерференционного поля трансформируются в фазу электрического сигнала. Измерение последней осуществляется с применением электронной аппаратуры. Использование указанного технического решения позволяет в значительной степени снизить погрешность измерений и расширить диапазон определяемых величин [1–7].

АНАЛИЗ ИНТЕРФЕРОМЕТРА СДВИГА

Для анализа функционирования системы обработки голографических интерферограмм с применением двухчастотного излучения необходимо конкретизировать вид используемого интерферометра сдвига и получить аналитическое выражение для разности фаз лучей, прошедших интерферометр. Из соображений виброустойчивости, а также простоты конструкции в работе предлагается использовать интерферометр Жамена, образованный двумя идентичными плоскопараллельными пластинами [8]. В [2–7, 9] приведены результаты анализа этого интерферометра в приближенном варианте. Точность, на которую претендует система, требует анализа интерферометра в строгом изложении.

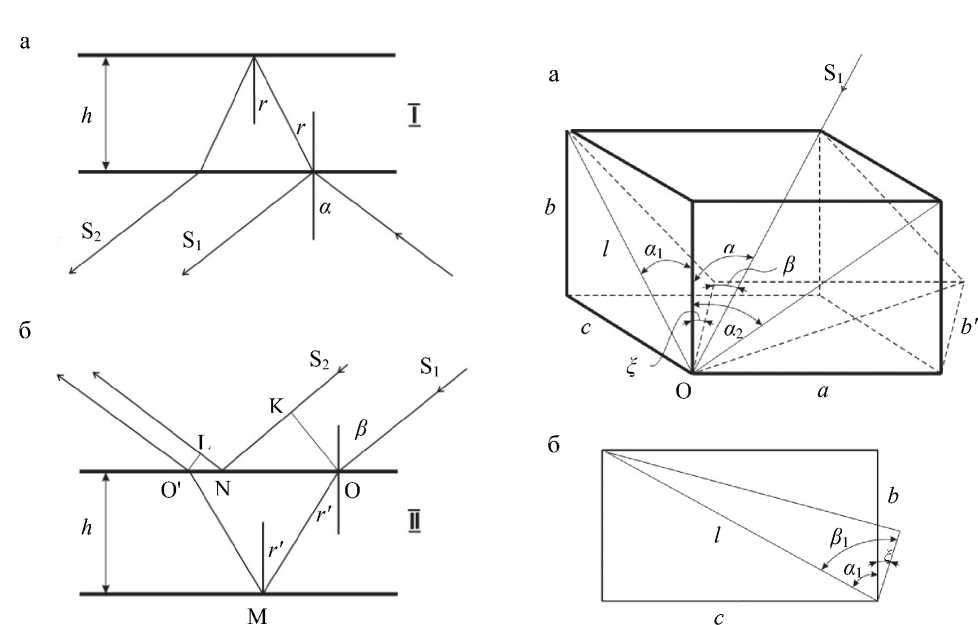
Рис. 1. Прохождение света через первую (а) и вторую (б) пластины интерферометра Жамена

Рис. 2. К расчету разности хода лучей в интерферометре Жамена

Разность хода лучей при прохождении интерферометра (рис. 1) определяется следующим выражением:

A = A i ( « 1 , а 2 ) + A_n ( a i , а 2 , ^ ) , (1)

где A I ( а 1 , а ₂ ) — разность хода лучей после первой пластины интерферометра; A II ( а 1 , а 2 , ^ ) — разность хода лучей после прохождения второй пластины интерферометра; α ― угол падения луча на первую пластину; α ₁ и α ₂ ― проекции угла α (рис. 2); ξ ― угол наклона второй пластины относительно первой.

Воспользовавшись рис. 1, запишем выражение для А , и A II . Из рис. 1 следует

А , = 2 hn/ cos r - 2 h tg r sin а = 2 hn cos r , (2) где h ― толщина пластины интерферометра; n ― показатель преломления материала пластины интерферометра; r ― угол преломления луча на первой пластине.

Из рис. 1, б, следует

A II = KN + NL - 2 n OM,        (3)

где

KN + NL = ON sin в + O'N sin в = = O'O sin в = 2 h tg r 'sin в, OM = h /cos r '.

Отсюда hn

AII = 2h tg r sin в - 2-----= cosr'

2 h

=------( sin r ^in в - n ) .

cos r '

Так как sin в = n sin r ', то

A II = - 2 hn cos r '.

В этих выражениях β ― угол падения луча на вторую пластину; r ' ― угол преломления луча во второй пластине.

Запишем выражение для суммарной разности хода:

A = A I + А II = 2 hn ( cos r - cos r ' ) .         (4)

Для нахождения неизвестной величины cos r ' произведем дополнительные геометрические построения (рис. 2).

Построим проекции угла падения α на две взаимноперпендикулярные плоскости, а также проекции угла падения на вторую пластину интерферометра на те же плоскости и найдем связь между этими проекциями, возникающую при повороте второй пластины интерферометра относительно первой на угол ξ , как показано на рис. 2.

Из рис. 2, а, найдем

Составляющие угла β можно определить, воспользовавшись рис. 2, б:

tg в = 4tg2 в + tg2 в2 , где в1 = a1 + E .

Следовательно, tg в = tg (a + E).

Для того чтобы определить

tg β ₂ ,

воспользуемся тригонометрическими формулами: b '

ctg ^в 2 = — ,

a где a = ctg α2

bb

---, d =-----. Отсюда

cos α ₁

( b tg « 1 ) ² + ( b tg a ₂ ) ² = ( b tg a ) ² .         (5)

Поделив все члены выражения (5) на b , получим b cos (a + E)

cos α ₁

.

tg ² a = tg ² a 1 + tg ² a ₂.

Учитывая также, что tg2 α1

sin a = —----, cos a = —2

tg a + 1            tg a + 1

запишем выражения для cos α и sin α :

cos a = .■,

4 tg ² a i + tg ² a 2 + 1

.       4 tg2 a + tg2 a sin a = ..

4 tg ² a + tg ² a 2 + 1

Используя выражения (7) и (8) запишем

Поэтому

cos (a, + E) ctg в2 =------------ ctg a 2, cos α1

cosα tg в2 =----7----tg a 2 .

cos ( a 1 + E )

Следовательно,

2              2      cos2α tg в = A tg (a1 + E ) + tg a2---77-----TV .

\                      cos ( a 1 + E )

Зная tg β , можно записать выражение cos r ' :

cos r ' =

cos r = a/1 - sin2 r =

sin ² α n ²

tg ² ( « 1 + E ) + tg ² a 2

tg ² a 1 + tg ² a n ² ( tg ² a 1 + tg ² a + 1 )

1 —г--------- n2 tg2 (a1 + E) + tg2 a2

cos ² α ₁

cos ² ( a 1 + E ) cos ² α

---77---+ 1

cos ( a 1 + E )

.

Аналогично можно записать выражение для cos r ':

cos r' = a /1 - sin ² r' = a 1

sin ² β

n ²

Таким образом, подставляя полученные выражения в (4), определим разность хода лучей, выраженную через проекции на две взаимноперпендикулярные плоскости:

tg ² β     _.

n2 (tg2 в +1)

A = 2 nh <

1 -     tg ² a 1 + tg ² a 2

n ² ( tg ² a 1 + tg ² a ₂ + 1 )

—

Воспользуемся рис. 2 и найдем tg β .

—

, —

tg 2 ( « 1 + £ ) + tg 2 « 2

cos ² α ₁

cos ² ( a , + ^ )

n ² tg ² ( a , + £ ) + tg ² a 2

cos ² α ₁

.

a ' 2i =

(2a,^ + £2 +,) , +

V ²

2 n ²

cos ² ( a , + £ )

+ 1

Из (9) и (,0) следует, что при s = 0, в , и в ₂ = a ₂. Поэтому

= a ,

= 1

—

2 a , ^ + ^ ² + , + °^

2 n ²

.

Следовательно,

A i ( a , , a 2 ) = A_n ( a , , a 2 , s = 0 ) .

Пусть A II = 2 hn A ' II , где

A 'ii =1M

—

2 n ²

, —

2 a , ^ + ^ ² + , + '2

2 n ²

X

A 'n =

, —

2 n ²

, —

tg ² ( a , + ^ ) + tg ² a 2

cos ² α ₁

cos ² ( a , + £ )

Учитывая малость

n 2 tg ² ( a , + ^ ) + tg ² a 2

cos ² α ₁

cos ² ( a , + £ )

+ ,

При разложении в ряд Маклорена для значений аргумента

cos ² a , ~ , — a ,² ,

tg ² ( ^a , ^— ^ M ^a , ^— ^ ) ² .

При a ₂ ~ 45 ° tg a ₂ ~ I . Следовательно, записать

(a, + ^ )2 +

, — a ,²

.

малых

можно

A 'ii =

—

, — ( a , + ^ ) 2

n ² ( a , + £ ) ² +

, — a ,²

.

, — ( a , + £ ) ²

+ ,

полученное выражение величин:

α ₁ и в ряд по

ξ , разложим

степеням

этих

A ' ii =a A

—

—

—

^α 1²

2 n ²

8 n ² 1

α ₁ ξ

—

—

—

2 n ²

ξ ²

2 n ² 1

—

2 n ²

4 n ² 1

—

.

2 n ²

Так как A ' I ( a , , a ₂ ) = A ' II ( a , , a ₂, ^ ) , то

A ' i = a ,

—

—

α ₁ ²

2 n ²

8 n ² 1

—

.

2 n ²

На основе предыдущих выражений запишем

Проведем выражения:

преобразования

A ' = A ' i — a ' ii =

α ₁ ξ

—

ξ ²

полученного

2 n ² 1

—

2 n ²

4 n ² 1

—

.

2 n ²

ii

Окончательно для разности фаз лучей, прошедших интерферометр сдвига, получим

=, —

n ² [ ( a , + ^ ) 2 — ( a ,

( a , + ^ ) 2 — ( a , + ^ ) 4 + , — a ,

+ ^ ) 4 + , — a ,² + , — ( a , +

=, —

2 a< 1 A 1 ,

ф = — 2 hn A' = иλ

π 2 hnαξ

Ь       +

2 n ² 1

—

n ² ( 2 — a ,² )

2 n ²

Так как

2 — a ,²    2

•

α ₁ ² ,

,     , a 2 )

— , + — , то пос

2 V 2 J

леднее выражение запишется в следующем виде:

где d _и

² π 2 hnξ ²

4 n ² 1

—

2 n ²

2 π

= —^a , d и + ф ио , λ

и ϕ _и0 ― соответственно смещение

и постоянный фазовый сдвиг, вносимые

интерферометром:

d и =

hξ

n 1

—

,

2 n ²

Ф и0 =

πhξ ²

ЛП. 17

2 n ²

Полученные выражения позволят провести анализ сигнала на выходе интерферометра.

ЗАКЛЮЧЕНИЕ

Получены основные математические соотношения для параметров выходного сигнала

Выведено аналитическое выражение для разности фаз световых лучей, прошедших интерферометр. Это позволит вычислять основные параметры интерферометра Жамена, которые влияют на точностные характеристики и диапазон измерений системы, и соответственно смещение и постоянный фазовый сдвиг, вносимые интерферометром.