Вывод формулы Беломестных-Теслевой из уравнения Грюнайзена

Автор: Дармаев М.В., Сангадиев С.Ш., Мантатов В.В.

Журнал: Вестник Бурятского государственного университета. Химия. Физика @vestnik-bsu-chemistry-physics

Статья в выпуске: 1, 2022 года.

Бесплатный доступ

Предлагается вывод формулы Беломестных-Теслевой, устанавливающий однозначную связь между коэффициентом Пуассона и параметром Грюнайзена, из известного уравнения Грюнайзена. Формула Беломестных-Теслевой, полученная ранее из иных исходных посылок, выводится с привлечением теории упругости и уравнения Леонтьева. Предлагаемый подход находит вполне удовлетворительное согласие с экспериментальными данными для ряда силикатных стекол и стеклообразных метафосфатов щелочноземельных металлов.

Уравнение грюнайзена, упругие свойства, скорости акустических волн, параметр грюнайзена, коэффициент пуассона, модуль сдвига, изотермический модуль объемного сжатия

Короткий адрес: https://sciup.org/148327683

IDR: 148327683 | DOI: 10.18101/2306-2363-2022-1-18-23

Текст научной статьи Вывод формулы Беломестных-Теслевой из уравнения Грюнайзена

Принято считать, что параметры теории упругости (модули упругости, коэффициент Пуассона) как гармонические линейные величины не должны быть связаны с ангармонизмом — с отклонением силы межатомного взаимодействия от линейной зависимости при смещении атома из равновесного положения. Тем не менее время от времени появляются работы, указывающие на наличие вполне определенной связи между упругими свойствами и параметром Грюнайзена γ — мерой ангармонизма [1]

pVB

где β — коэффициент объемного теплового расширения, V — молярный объем, B –изотермический модуль объемного сжатия, C V — молярная теплоемкость при постоянном объеме.

Так, например, Беломестных и Теслевой [2] установлено, что параметр Грюнайзена γ является однозначной функцией коэффициента Пуассона μ — параметра теории упругости з / 1 -+- ц \ причем установлено достаточно строго с привлечением известных положений теории упругости, термодинамики и физической акустики. Они показали, что параметр Грюнайзена определяется исключительно по скоростям продольной (vL) и поперечной (vs) акустических волн:

3 (vl/vs У - 4

2 [(Viks )2 + 2

Беломестных и Теслева [2], используя в формуле (3) известные соотношения физической акустики [3]

, = E (1 — а)

^VS V ² P ⁽ ¹ ⁺ А )

L р1+ + А )(1- 2^) ’

в 2004 г. получили уравнение (2), однозначно связывающее параметр Грюнайзе-на с коэффициентом Пуассона. Примечательно то обстоятельство, что такая сравнительно простая формула (2) находится в удовлетворительном согласии с уравнением Грюнайзена (1) [2].

Вывод формулы Беломестных–Теслевой (2) из уравнения Грюнайзена (1). Умножив числитель и знаменатель уравнения Грюнайзена (1) на модуль сдвига G и принимая во внимание известную взаимосвязь упругих модулей G и B [1]

В 2 1 + ^z \ получаем следующую модификацию уравнения Грюнайзена (1)

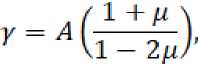
где введено обозначение

Используя соотношение Леонтьевна [4]

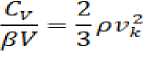
и модуль сдвига G = ρ v s ² , множитель A (6) представим в виде отношения скоростей звука

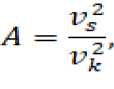
где v k ² — квадрат среднеквадратичной скорости звука [4]

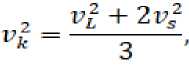
v L и v s — скорости продольной и поперечной упругих волн, соответственно, ρ — плотность.

Из равенства (8) с помощью выражения (9) и известной формулы теории упругости [1]

/v_LV 2 — 2/z

\v_s / 1 — 2// (10)

находим связь множителя A с коэффициентом Пуассона μ

3 /1 - 2/zx

2 \2 — 3/2/ (11)

Расчет параметра A по формулам (8) и (11) показывает согласованные значения (табл. 1). Для силикатных стекол, приведенных в таблице значения, рассчитанные по разным формулам достаточно близки. Для стеклообразных метафосфатов щелочноземельных металлов значения коэффициента A по формулам (8) и (11) совпадают с точностью до сотой доли единиц, тангенс угла наклона графика A (8) — A (11) равен единице.

Примечательно то обстоятельство, что с учетом данного соотношения (11) модифицированное уравнение Грюнайзена (5) переходит в формулу Беломест-ных–Теслевой (2)

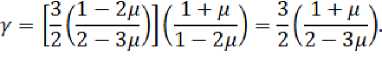
Таблица 1

Расчет множителя A по формулам (8) и (11) для силикатных стекол R 2 O–SiO 2 (R = Na, K)[5] и стеклообразных метафосфатов щелочноземельных металлов [6]

№		μ	v L , м/с	v s , м/с	v k , м/с	A (8)	A (11)
Na 2 1	O — SiO 2 Содержание Na 2 O, мол.% по синтезу: 13	0,205	5233	3378	4091	0,68	0,64
2	16	0,218	5115	3275	3984	0,68	0,63
3	17	0,225	5054	3222	3929	0,67	0,62
4	20	0,235	12133	7705	9415	0,67	0,61
5	26	0,245	4835	3070	3752	0,67	0,60
6	30	0,255	4844	3052	3746	0,66	0,60
7	33,3	0,255	4906	3103	3800	0,67	0,60

1	Содержание K 2 O, мол.% по синтезу: 13	K 2 O — SiO 2			3747	0,67	0,62
1	Содержание K 2 O, мол.% по синтезу: 13	0,230	4820	3073	3747	0,67	0,62
2	15	0,225	4759	3035	3700	0,67	0,62
3	20	0,250	4550	2889	3531	0,67	0,60
4	25	0,270	4463	2801	3445	0,66	0,58
	Стеклообразные метафосфаты щелочноземельных металлов
1	0,51MgO·0,49P 2 O 5	0,233	5267	3110	3962	0,62	0,62
2	0,50MgO·0,50P 2 O 5	0,233	5264	3108	3959	0,62	0,62
3	0,49MgO·0,51P 2 O 5	0,233	5289	3121	3977	0,62	0,62
4	0,51CaO·0,49P 2 O 5	0,264	5051	2858	3735	0,59	0,59
5	0,50CaO·0,50P 2 O 5	0,267	5086	2869	3756	0,58	0,58
6	0,49CaO·0,51P 2 O 5	0,265	5051	2857	3734	0,59	0,59
7	0,51SrO·0,49P 2 O 5	0,274	4603	2568	3385	0,58	0,58
8	0,50SrO·0,50P 2 O 5	0,273	4610	2577	3393	0,58	0,58
9	0,49SrO·0,51P 2 O 5	0,271	4612	2584	3397	0,58	0,58
10	0,50BaO·0,50P 2 O 5	0,288	4178	2278	3046	0,56	0,56
11	0,49BaO·0,51P 2 O 5	0,286	4186	2291	3056	0,56	0,56

Таким образом, с привлечением соотношения Леонтьева (7) и теории упругости из уравнения Грюнайзена (1) можно вывести формулу Беломестных– Тес-левой (2), которая была получена из иных исходных посылок [2].

Обратим внимание на то обстоятельство, что коэффициент A в выражении (8) показывает, какую долю составляет упругая энергия Δ U = ρ vs ² V , необходимая для деформации сдвига, от средней энергии межатомного взаимодействия и = pv^V

_v* pv$V GV AU

^{A —} ~ pv^V ^{— —} (12)

Для стеклообразных твердых тел уравнение (5) было получено ранее со следующей интерпретацией множителя A [7]

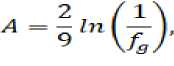
где f g — объемная доля флуктуационного свободного объема, замороженная при температуре стеклования T g . Величина f g у стеклообразных систем одного класса является фактически универсальной величиной f g ≈ const [7]. Логарифм данной величины тем более слабо зависит от состава аморфных веществ в рамках одного класса. Оценка A по этой формуле (13) дает фактически константные значения, по крайней мере, у стекол одного структурного типа и по порядку величины согласуется с результатами расчета по соотношениям (8) и (11). Для натриевосили-катных Na 2 O–SiO 2 и калиевосиликатных K 2 O–SiO 2 стекол значение объемной доли флуктуационного свободного объема f g ≈ const ≈ 0,028, а величина A , рассчитанная по формуле (13), приблизительно равна 0,79.

Значения параметра Грюнайзена для металлов, рассчитанные по уравнению Грюнайзена (1) и Беломестных-Теслевой (2) также находятся в удовлетворительном согласии (табл. 2).

Некоторые отклонения значений для твердых тел, вероятно, обусловлены разбросом значений γ, полученных разными исследователями. Причина этих отклонений также возможно заключается в анизотропии рассматриваемых в табл. 2 систем, так как более согласованные данные наблюдаются для ряда квазиизо-тропных щелочногалоидных кристаллов с центральными силами межатомного взаимодействия.

Таким образом, предлагаемый вывод из уравнения Грюнайзена (1) формулы Беломестных-Теслевой (2), которая устанавливает связь параметра Грюнайзена с коэффициентом Пуассона, находит вполне удовлетворительное согласие с экспериментальными данными.

Таблица 2 Сравнение результатов расчета параметра Грюнайзена γ по уравнениям (1) и (2) (использованы данные [2, 8]).

№	Элементы и соединения	µ	γ
№	Элементы и соединения	µ	Грюнайзен (1)	Беломестных–Теслева (2)
1	LiF	0.214	1.34	1.34
2	NaCl	0.243	1.46	1.47
3	Fe	0.292	1.68	1.72
4	Al	0.340	2.11	2.05
5	Ag	0.379	2.40	2.40
6	NaNO 3	0.257	1.31	1.53
7	Pd	0.374	2.40	2.35
8	Au	0.420	2.80	2.88

Список литературы Вывод формулы Беломестных-Теслевой из уравнения Грюнайзена

Ландау Л. Д., Лифшиц Е. М. Теория упругости. 3-е изд. Москва: Наука, 1965. 204 с. Текст: непосредственный.
Беломестных В. Н., Теслева Е. П. Взаимосвязь ангармонизма и поперечной деформации квазиизотропных поликристаллических тел // ЖТФ. 2004. Т. 74, № 8. С. 140-142. Текст: непосредственный. EDN: RDASSD
Францевич И. Н., Воронов Ф. Ф., Бакута С. А. Упругие постоянные и модули упругости металлов и неметаллов. Справочник. Киев: Наукова думка, 1982. 286 с. Текст: непосредственный.
Леонтьев К. Л. О связи упругостных и тепловых свойств веществ // Акуст. журн. 1981. Т. 27, вып. 4. С. 554-561. Текст: непосредственный.
Мазурин О. В., Стрельцина М. В., Швайко-Швайковская Т. П. Свойства стекол и стеклообразующих расплавов: справочник. Ленинград: Наука, 1973. Т. 1. 444 с. Текст: непосредственный.
Скорость ультразвука в стеклообразных метафосфатах щелочноземельных металлов / Е. А. Гурович, А. А. Ильин, А. А. Пронкин, М. Е. Стржалковский // Физика и химия стекла. 1979. Т. 5, № 3. С. 383-384. Текст: непосредственный.
Сандитов Д. С., Бартенев Г. М. Физические свойства неупорядоченных структур. Новосибирск: Наука, 1982. 259 с. Текст: непосредственный.
Беломестных В. Н. Акустический параметр Грюнайзена твердых тел // Письма в ЖТФ. 2004. Т. 30б, вып. 3. С. 15-19. Текст: непосредственный. EDN: RDBIMD

Еще

Статья научная