Вывод на орбиту и сближение космического робота с геостационарным спутником

Информационные спутники (связи, метеорологического наблюдения Земли) на геостационарной орбите (ГСО) имеют потребную длительность службы до 25 лет при наличии технического обслуживания с помощью космических роботов-манипуляторов (КРМ), в частности дозаправки топливом их электрореактивных двигательных установок (ЭРДУ). В современной космонавтике наблюдается регулярная тенденция к увеличению массы полезной нагрузки информационных спутников на ГСО. Ограничения на допустимую массу затрат топлива при выведении крупногабаритного космического

аппарата (КА) на ГСО приводят к проблеме «до-выведения» КА от переходной орбиты (ПО) до геостационарной с помощью бортовой ЭРДУ [1]. В этой связи проблемные вызовы состоят в использовании электрореактивной тяги при как выводе и удержании информационного спутника на ГСО, так и перелётах обслуживающего его КРМ.

Для выведения геостационарных КА применяются ракеты-носители (РН) с разгонным блоком, который способен осуществить необходимые манёвры для перевода КА с эллиптической геопереходной орбиту (ГПО) на ГСО. Такая схема требует от КА наличия собственной химической реактивной двигательной установки (ХРДУ) большой тяги (БТ), что не является эффективным решением с точки зрения стартовой массы КА: масса топлива для «до-выведения» КА на ГСО может составлять до 50 % от стартовой массы КА, в зависимости от РН и условий старта. В то же время, малая тяга электрореак-тивных двигателей (ЭРД) в составе ЭРДУ многократно увеличивает время «до-выведения» спутника, а также время нахождения КА в зоне наиболее опасного внутреннего радиационного пояса Земли на высотах полета от 2000 до 12000 км, что предъявляет повышенные требования по радиационной защите как полезной нагрузки, так и служебных систем, в том числе панелей солнечных батарей (СБ). Поэтому для успешной доставки на ГСО космического аппарата с минимальными затратами топлива за приемлемое время рационально применять комбинирован- ную схему, основанную на поочерёдной работе химической и электрореактивной двигательных установок: ХРДУ БТ используется для формирования переходной орбиты, по которой спутник быстро проходит зону внутреннего радиационного пояса Земли, а ЭРДУ – для последующего «до-выведения» спутника на ГСО.

Для реализации такой схемы в последние два десятилетия интенсивно выполнялись исследования и разработки как за рубежом [2], так в России – организациями Роскосмоса, академическими институтами и профильными университетами. Первые спутники США на базе платформы 702SP фирмы Boeing с электрореак-тивным «до-выведением» с эллиптической ГПО (400 ^х 63000) км были запущены в 2015 г. При этом масса ксенона, используемого для «до-выведения» указанных КА, составляла « 5 % их стартовой массы, что в десять раз меньше, чем при использовании обычной ХРДУ. АО « ИСС им. акад. М.Ф. Решетнева » также приступило к практическому решению этих проблем, здесь были проведены необходимые инженерные обоснования [3] и первые запуски – российские спутника связи Экспресс-AM5/AM6 «до-выводились» на ГСО с помощью собственной ЭРДУ в 2013-2014 гг. и 2015 г. соответственно. При этом в топливном бюджете ЭРДУ указанных КА были учтены затраты как на «до-выведение» длительностью несколько месяцев, так и на удержание этих спутников в заданных точках ГСО с эпизодической разгрузкой электромеханических приводов от накопленного кинетического момента (КМ) в течение гарантированного срока службы до 15 лет.

В статье рассматриваются три задачи: (i) выбор отечественных реактивных двигательных установок (РДУ) космического робота и анализ их топливных бюджетов для выведения КРМ с массой « 3000 кг по комбинированной схеме на ГСО с дальностью до цели 500 м; (ii) выбор структуры ХРДУ малой тяги (МТ) и электромеханических приводов системы управления движением (СУД) КРМ для выполнения его сближения с целью до дальности 100 м; (iii) синтез законов наведения и управления КРМ, нелинейный анализ динамики СУД при таком сближении.

ВЫВЕДЕНИЕ КОСМИЧЕСКОГО РОБОТА НА ГЕОСТАЦИОНАРНУЮ ОРБИТУ

В таб. 1 и таб. 2 представлены основные характеристики отечественных реактивных двигателей (РД), выбранных для применения на борту КРМ. При этом

. ХРДУ БТ реализуется одним РД ДСТ-200А при создании тяги величиной 200 Н по оси + O r у связанной с корпусом КРМ системы координат (ССК) O_r xyz с началом в полюсе O_r , который при исходном состоянии совпадает с центром масс робота C_r ;

• .    ХРДУ МТ строится по симметричной схеме на основе восьми РД ДСТ-25 ;

• .    ЭРДУ реализуется двумя РД СПД-140Д с общей тягой 0.58 Н по оси + O r у ССК.

Будем считать, что вывод КРМ с начальной массой m i = 6300 кг на эллиптическую ГПО (200 х 35786) км с наклонением 51.6 град выполняется запуском с космодрома Байконур посредством РН Протон-М с разгонным блоком Бриз . Применяемая стратегия последующего вывода КРМ на ГСО содержит следующие орбитальные манёвры:

Таблица 1. Характеристики химических РД КБХМ им. А.М. Исаева

Тип двигателя	Уд. импульс, [м/с]	Тяга, [Н]	Топливо/окислитель	Масса, [кг]
ДСТ-200А	2940	200	НДМГ/АТ	1.7
ДСТ-25	2790	25	НДМГ/АТ	0.8

Таблица 2. Характеристики электрореактивного двигателя ОКБ Факел

Тип двигателя	Уд. импульс, [м/с]	Тяга, [Н]	Раб.тело	Мощн. [Вт]	Масса, [кг]
СПД-140Д	17363.7	0.29	Ксенон	4500	8.5

Таблица 3. Топливный бюджет и длительности орбитальных перелётов КРМ

	Перелётный манёвр	V h , [м/с]	Тип РДУ	m w , [кг]	m f ,[кг]	T „ > [с ут ]
1 a	Уменьшение наклонения геопереходной орбиты	1604	ХРДУ БТ	2650	3650	4-8
1 b	Подъём перигея ГПО до 10000 км	307	ХРДУ БТ	362	3288	1
2	Переход КРМ на ГСО в окрестность цели с дальностью 500 м	773	ЭРДУ	270	3018	122
3	Сближение КРМ с целью до дальности 100 м	21	ХРДУ МТ	24	2994	≈ 0.02

• 1.    переход КРМ на ПО с помощью ХРДУ БТ при последовательном выполнением этапов (1 a ) обнуления наклонения ГПО и (1 b ) подъёма её перигея до 10000 км;

• 2.    переход КРМ с промежуточной орбиты на ГСО с использованием ЭРДУ с дальностью до цели (геостационарного спутника) 500 м;

• 3.    переход КРМ с использованием ХРДУ МТ в окрестность цели с дальностью 100 м.

Оценки изменения массы КРМ и длительности его перелетных манёвров, полученные на основе известных методов динамики управляемого космического полёта, приведены в таб. 3, где V _h – характеристическая скорость манёвра, m _w – затраты топлива (рабочего тела), m _f – масса КРМ при завершении манёвра, T _m – его длительность. Здесь проблемные вызовы состоят в энергообеспечении ЭРДУ при наведении крупногабаритных панелей СБ на Солнце, в управлении как ориентацией КРМ, так и ЭРДУ с минимизацией затрат её рабочего тела при орбитальном перелёте.

СТРУКТУРА ПРИВОДОВ СУД

Представленная на рис. 1 схема ХРДУ МТ строится на основе восьми РД ДСТ-25 по симметричной схеме с широтно-импульсной модуляцией (ШИМ) тяги 25 Н каждого РД и позволяет одновременно создавать векторы импульсов внешней силы и внешнего момента произвольных направлений в ССК космического робота.

На рис. 2 приведена минимально-избыточная схема силового гироскопического кластера (СГК) на основе четырёх гиродинов (ГД), которая далее используется при значении собственного КМ h _g = 100 Нмс каждого ГД.

Отметим, что здесь можно применить и кластер четырёх двигателей-маховиков по схеме General Electric , однако СГК имеет ряд динамических преимуществ при решении основных целевых задач КРМ.

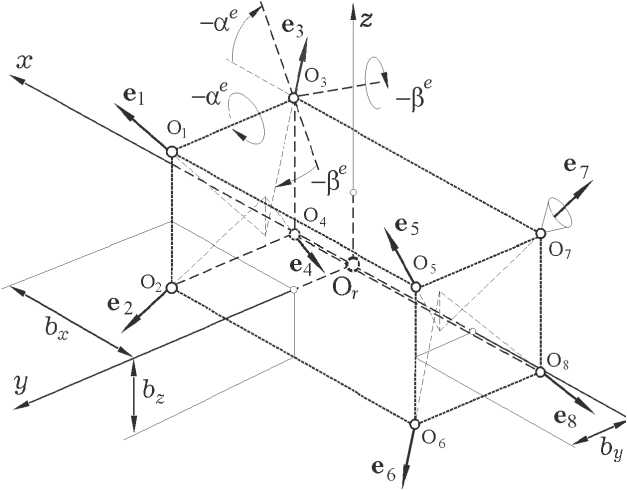
Рис. 1. Схема РДУ на осно в е 8 РД мал о й тяги

МОДЕЛИ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ

Для описания перемещения центра масс КА и его углового движения применяются геоцентрическая экваториальная I _⊕ и солнечноэклиптическая I _s инерциальные системы координат (ИСК). В ИСК I _⊕ ( O _⊕ XⁱYⁱZⁱ ) орт e _s направления из центра Солнца к центру Земли O _⊕ имеет вид e _s^I( t ) = [ -ε _e]₁ [ -ρ _s( t )] ₃ {1,0,0} , где ε _e представляет угол наклона оси вращения Земли к плоскости эклиптики, Р , ⁽ t ⁾ = р ” +® _s( t - t о ) , Р 0 = Р s ^{( 1} 0 ) • ¹ 0 ^- некоторый начальный момент времени, ω _s – средняя угловая скорость обращения Земли вокруг Солнца. Здесь и далее используются общепринятые обозначения col( ⋅ ) = { ⋅ } , line( ⋅ ) = [ ⋅ ] , 〈⋅ , ⋅〉 , ( ⋅ )^t , [ a × ] и ^о ,~ для векторов, матриц и кватернионов, матрицы [ α ] _i элементарного поворота вокруг i -ой оси на угол α , i = 1,2,3 ≡ 1 ÷ 3 , а также C _α ≡ cos α , S _α ≡ sin α и дискретные значения вектора x ( t_k ) ≡ x _k , k ∈ N₀ ≡ [0,1,2,...) .

Используется Гринвичская система координат (ГСК) G _⊕ , связанная с Землей, которая вращается с угловой скоростью ω ^e . Положение ГСК G _⊕ относительно ИСК I _⊕ определяется углом ρ _e ( t ) = ρ _e ⁰ +ω ^e( t - t ₀) , где ρ e ⁰ = ρ e ( t 0 ) – угловое положение Гринвичского меридиана относительно направления на точку весеннего равноденствия Y при 1 = 1 ₀ и to e - модуль вектора ю ^е = {0,0, to ^e} угловой скорости вращения Земли.

Орбитальная система координат (ОСК) O (O x ^o y ^o z ^o) КА с ортами o ₁ , o ₂ , o ₃ имеет следующие направления осей и связанных с ними ортов: ось O x ^o и орт o ₁ совпадают по направлению с ортом r ^o вектора r _^ ( t ) расположения центра масс КА в ИСК I _⊕ ; ось O z ^o и орт o ₃ = n ^o направлены по нормали n ^o к плоскости орбиты; ось O y ^o с ортом o ₂ = τ ^o при трансверсали τ ^o , перпендикулярной оси O x ^o . Вектор угловой скорости ω ^o орбитального движения КА в ОСК определяется как to o = to o ( 1 ) n ^o = V ( 1 ) n ^o , где истинная аномалия ν ( t ) отсчитывается от перигея орбиты π .

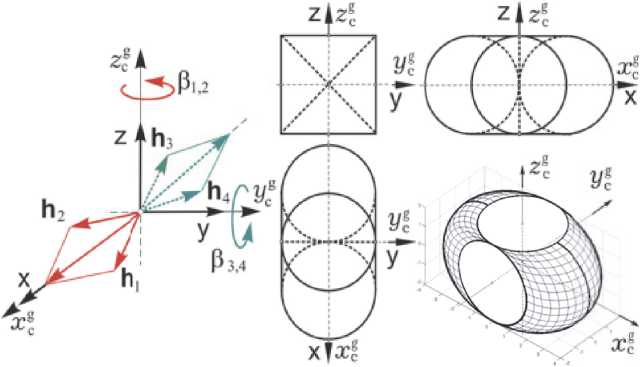
Рис. 2. Схема СГК на основе 4 гиродинов

Если считать КА твёрдым телом с массой m и тензором инерции J , то при стандартных обозначениях модель его пространственного движения в ИСК, но в проекции на оси ССК O xyz с полюсом O , совпадающим с центром масс C , имеет вид

г * - и х r = v ; m( v * + и х v ) = P ^e + F ^d;

Л = Л о to/2; J с + их G = Mg + Me + Td.

представляется нелинейным соотношением ■

M k ( t ) = — h g A h ( P ( t ) u k ( t ) ; P ( t ) = u k ( t ) , где вектор-столбец p = {p _p } и матрица Якоби a h ( p ) =d h ( p ) /ap .

НАВЕДЕНИЕ ПРИ СБЛИЖЕНИИ КРМ С ГЕОСТАЦИОНАРНЫМ СПУТНИКОМ

Здесь кватернион Λ представляет ориентацию КА в ИСК, вектор G = J ω + H , где H является вектором кинетического момента СГК, векторы P ^e , M ^e и M ^g = — H представляют соответственно управляющие силы РДУ, моменты РДУ и СГК, F ^d и T ^d - векто-

ры внешних возмущающих сил и моментов, представленных в ССК, и используется символ ( • ) * локальной производной по времени. Кватерниону Л = ( X 0 , X ) , Х = { X i } , соответствует матрица C ( Л ) = I ₃ — 2[ X x ] Q t ( X ) , где Q ( X ) = I ₃ X₀ + [ X x ] . Ориентация ОСК в ИСК определяется кватернионом Л ⁰ с уравнением

Л ⁰ = Л ⁰ о Ю ⁰/2 .

В схемe ХРДУ МТ на рис. 1 положения ортов e p , p = 1 ^ 8 по осям сопел РД определяются углами a ^e, P e • Вектор р _p точки O _p приложения вектора тяги p -го РД определяется параметрами b_x , b y , b_z • Каждый РД имеет ШИМ тяги p_p ( t ) с нелинейным непрерывно-дискретным описанием

pp ( t ) = P m PWM( t — TU ,ts T m ,V pr ) V t E [ ts , ts + 1 ) при периоде T U и запаздывании T u . Здесь P^m является номинальным значением тяги, одинаковым для всех РД, t_{s + 1} = t_s + T U , t s = sT U; , s e N₀ = [0,1,2,...) и функции

PWM( t,t s , T m ,V ps ) =

/ signv ps 0

t ^{G [} Ms ^{+ T} ps X t ^{G [} t s ^{+ T} ps , t s + 1X

t (t ) = ps m

<

M TZ,\v

ps

\)

\ ^V ps I - ^T m ^; \ ^V ps \ > ^T m •

В ССК векторы тяги восьми РД вычисляются по соотношению p _p = - p_p e _p , а векторы тяги P ^e и момента M ^e РДУ - по формулам P ^e = S p p ( t ) и M ^e = E [ p p X ] p p ( t )•

Столбец H ( P ) = h_g 2 h _p ( в _p ) представляет вектор КМ СГК (рис. 2), где | h _p | = 1 , p = 1 ^ 4 и h_g является постоянным собственным КМ каждого ГД. Считая близкими командные u p и фактические в _p ( t ) угловые скорости ГД, при цифровом управлении u ^g ( t ) = {и р _д ( t )}, u^g_pk ( t ) = u pk V t e [ t_k , t_{k + 1}) в моменты времени t k = ^kTu ^с периодом ^Tu , tk + 1 = tk ⁺ T , ^{k E N}0 , вектор M ^g = {M g } управляющего момента СГК

Будем считать, что в некоторый начальный момент времени t i в ИСК известны значения векторов расположения и скорости поступательного движения КРМ r r ( t i ) , v _r ( t i ) (нижний индекс r , robot ) и цели r _t ( t i ) , v _t ( t i ) (нижний индекс t , target ). По значениям векторов r _t ( t i ) , v _t ( t i ) на основе известных соотношений [4] выполняется прогноз расположения r t ( t ) = r _t ^p ( t ) и скорости v _t ( t ) = v p ( t ) полюса O _t цели на интервале времени t e [ t i , t _f] заданной длительности T_m = t _f — t i , а также значения векторов r t ( t _f) и v _t ( t _f) в момент времени t _f .

При введении опорной круговой орбиты радиуса rr (ti) = const в плоскости земного экватора удобно рассматривать движение КРМ в малой окрестности такой орбиты с использованием цилиндрической системе координат (ЦСК) [4]. Здесь координатами являются значения радиали r и угла u её отклонения от произвольного направления, например от оси OeX1 ИСК, в плоскости опорной орбиты, а также значения бокового смещения z в направлении, ортогональном этой плоскости. Для принятой опорной орбиты координаты и скорости поступательного движения КРМ в ИСК определяются соотношениями г, ={rCu; rSu; z}; (2) vr = {r Cu - rSu ii; r Su + rCuii; Z}^

Пусть w r , w t и w^z представляют соответственно радиальную, трансверсальную и боковую компоненты вектора управляющего ускорения при движении КРМ, а µ – гравитационный параметр Земли. Синтез закона наведения КРМ при поступательном манёвре его сближения с геостационарным КА (рис. 3) в центральном гравитационном поле на интервале времени

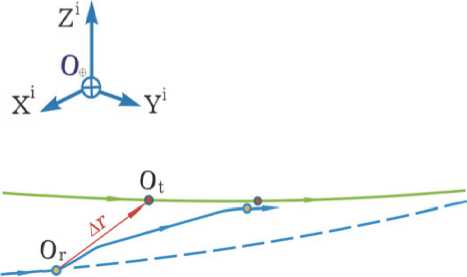
Рис. 3. Схема сближения КРМ с КА на ГСО

t e [ t i , t _f ] выполняется для модели движения космического робота

• 2             2 r,

• r — ru + ц / r = w ;

rU + 2 ru = w ;                 (3)

• 3 z

z + Ц z/r =w при краевых условиях по орбитальным переменным в ЦСК в виде vr (tд = ( vr (tJ, er> ,V (tf) = (v t (ta, er>;

V(t i ) = < v r ( t J, e t > , V ( t f ) = ( v _t(t f ), e f > ;

v z ( t i ) = < v _r ( t i ), e Z > , v z ( t f ) = ( v t ( t f ), e f > ;

u ( t i ) = ф^ u ( t f ) = ф i + arccos( ( e r , e f > ), где орты e с различными индексами вычисляются по соотношениям

• < = ^r r ( t i⁾ / r r ( t i⁾ ; ^e f = г ⁽ t a / r t ⁽ t f⁾ ;

• ^e = ^v r ⁽ t i^)/ v_r ⁽ t D; ^e f = ^v t ⁽ t f^)/ v t ⁽ t f );