Вывод уравнений движения механизма с четырьмя степенями свободы при ударном нагружении

В работе [1] исследован установившийся режим движения батанного механизма ткацких станков типа АТ с учетом упругости коленчатого вала и бруса батана, а в данной работе рассматривается удар батана в замки (рис. 1 a) – мгновенный останов машины на полном ходу при максимальной скорости батана по требованиям технологии ткачества [2]. При этом из-за упругости звеньев механизма удар начинается с левой замочной пружины механизма (рис.1 b). Этот процесс условно можно разделить на следующие основные этапы: 1) движение механизма при сопротивлении левой замочной пружины до начала удара в правую замочную пружину; 2) движение механизма при сопротивлении обеих замочных пружин: а) до крайнего переднего положения механизма; б) в обратном направлении до нарушения контакта с правой пружиной; 3) последующее движение механизма, состоящее из ряда этапов, носящее затухающий характер в силу рассеивания энергий.

Наибольшие усилия в звеньях механизма при ударе в замки появляются во время второго этапа в крайнем переднем положении механизма, поэтому здесь исследуются только первые два этапа. Начальными условиями при рассмотрении этих этапов соответственно являются конечные условия установившегося движения перед началом удара батана в замки и конечные условия первого этапа. При решении задачи удара местные деформации соударяющихся звеньев механизма считаются малыми и не учитываются, учитываются только общие деформации упругих звеньев: коленчатого вала, бруса батана и замочных пружин.

Рассмотрим движение батанного механизма во время удара в обе замочные пружины с учетом крутильной упругости коленчатого вала между кривошипами и изгибной упругости бруса батана между шатунами [1]. Принятая динамическая модель механизма приведена на рисунках 1 b, c и представляет собой шестимассовую систему с четырьмя упругими звенья- ми, имеющую четыре степени свободы и отличающуюся от расчетной схемы установившегося движения тем, что на нее дополнительно наложены две упругие связи (замочные пружины) и отключен двигатель станка.

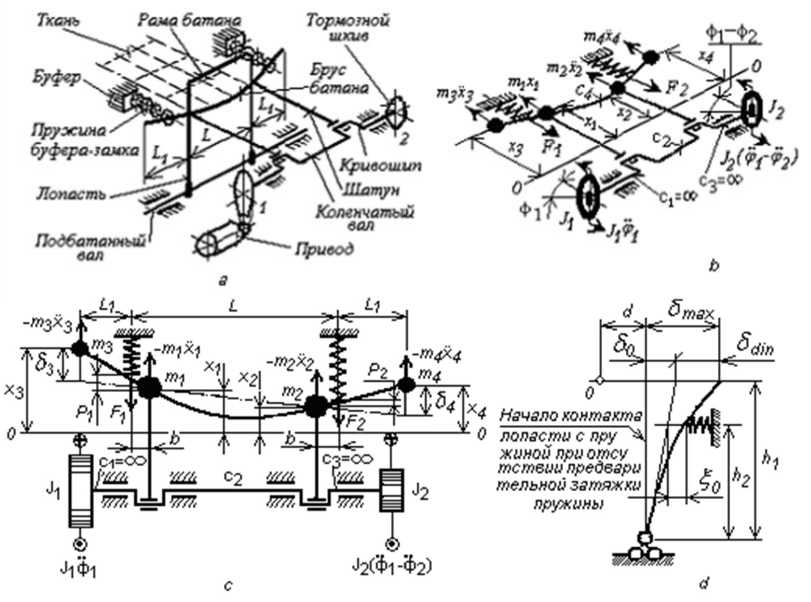
Рис.1. Принципиальная схема ( a ) и динамическая модель батанного механизма в момент начала удара в замки (b, c) и деформация лопасти (d)

Если в расчетной схеме (рис. 1 b, с) положить F 2 = 0, то получим расчетную схему для первого этапа удара в замки. Хотя система имеет четыре степени свободы и ее положение в любой момент времени вполне определяется четырьмя обобщенными координатами, удобно при выводе уравнений, описывающих движения масс системы, пользоваться шестью координатами по количеству масс. Поскольку установившееся движение и удар батана в замки являются непрерывным процессом, то для математического моделирования удара используется та же система координат, что и в работе [1]: х 1 , х₂, х₃, х₄ - перемещение соответствующей массы от ее заднего крайнего положения 0 - 0 в момент начала движения (рис. 1 b, c); Ф 1 - угол поворота левого кривошипа; ф ₂ - упругий угол поворота правого кривошипа относительно левого за счет упругости коленчатого вала. Массы m ₃ и m ₄ являются приведенными массами при рассмотрении свободных колебаний рамы батана [3].

Остальная масса рамы батана с соответствующим приведением включена в массы m 1 и m ₂; J 1 и J ₂ - соответственно приведенный момент инерции деталей механизма, связанных с левым и правым концом коленчатого вала; F 1 и F 2 - приведенные к оси бруса батана силы упругости пружин и лопастей; c ₂ - коэффициент крутильной жесткости коленчатого вала между кривошипами; c 4 - изгибная жесткость бруса батана; R - радиус кривошипа; l - длина шатуна; L - пролет бруса; L 1 - длина консоли бруса. Принято m 1 = m ₂ = const, m ₃ = m ₄ = const, J 1 = const, J ₂ = const .

Ударная нагрузка воспринимается буфером, пружина которого имеет предварительную затяжку [2]. Для вывода уравнений движения механизма необходимо предварительно найти приведенную к оси бруса силы упругости пружин и лопастей F1 и F2 . Перемещения точек h приложения сил Fi и F2 (рис. 1 d) равны 5тях = 5iiп + 5q, где 50 = — ^ - заданная величина max n             0 h2 0

перемещения точек F 1 и F 2 за счет предварительной затяжки пружины ^ 0 . Динамические деформации лопасти и пружины 5 din имеют вид:

bb 51 din   (1 j ) X1 + r X3   d 1; L1      L1 bb 5 2din = (1 -   >x2 + , X4 - d2, LL а выражения для определения перемещений точек приложения сил F1 и F2

принимают вид:

b      b      h 1 5 1max = (1 - y) X1 + yX 3 + y^0 - d 1 ; L 1       L 1       h 2 b       b      h 1 5 2max (1T ) X 2 + TX 4 + , ^ 0 d 2 . L 1        L 1       h 2

Формулы для определения силы упругости F 1 и F 2 , приведенные к оси бруса, имеют

вид:	F = [(1 - b- ) x , + bx з +   i , - d ; L 1       L 1       h 2 F 2 = [(1 - b ) x 2 + bx 4 + hL^, - d 2 ] c „, . L 1        L 1       h 2

Жесткость замочной пружины и лопасти, приведённые к оси бруса батана, определяется выражением:

cлсрh2 CnP =     2        2 , c л h1 + c р h h2 где cл - изгибная жесткость лопасти; cр - жесткость замочной пружины.

Движение массы m ₁ (рис. 1 b, с) от ее крайнего заднего положения описывается уравнением:

R 2 X 1 = R (1 - cos Ф 1 ) - "^s^n Ф 1 .                                    (1)

Движение массы m ₂ (рис. 1 b, c) описывается уравнением:

R 2                   R 2 x 2 = R (1 - cos Ф 1 ) - "^"sin2 Ф 1 - ( R sin Ф 1 - ”2/” sin 2 Ф 1 ) Ф 2 .                  (2)

Рассмотрим движения масс коленчатого вала (рис. 2 b) с моментами инерции J ₁ и J ₂ , которые описываются уравнениями:

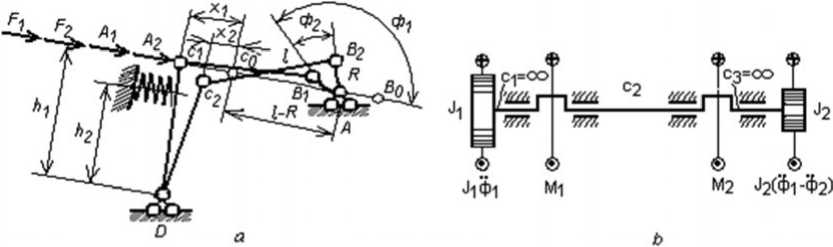
Рис. 2. Расчетная схема кривошипно-шатунного механизма ( а ) и коленчатого вала ( b ) в момент начала удара

Моменты M 1 и M2 выражаются через реактивные силы A1 и A2 бруса батана на четы- рехзвенник (рис. 2 а) на основании принципа возможных перемещений:

R ²

М i = A i ( R sin ф - -^- sin 2 ф 1 )

R ²

M 2 = A 2 ( R sin Ф 1 --sin 2 0 i

Реакции A ₁ и A ₂ определяются из условия равновесия бруса батана, находящегося под действием сил инерции приведенных масс и приведенных к оси бруса сил сопротивления замочных пружин и лопастей F 1 и F 2 (рис. 2 а ):

A1 = mx L b + (1 + y-) m 3x3 - -1- m 4 L F2; A 2 = m 2 x L b 2 + (1 + -^1) m 4 x4 - L m3x3 + (1 + L)F2 - —F - L1 Fi = [(1 - bb — ) x. +--x-> - L 1 1   L1  3 h d 1 + -г 5g] cnp; h2 ,                  (5) F2 = [(1 - bb — ) x2 +--x« - L 1 2 L1 4 d2 + 71 5g] Cnp, h2 где di = d 2= d - расстояние точки приложения силы F1 и F2 от крайнего заднего положения 0-0 до положения в момент начала удара; 50 - величина предварительной затяжки замочной пружины (рис. 1 d).

После подстановки выражений (4) в соотношения (3) с учетом (5) уравнения движения масс коленчатого вала принимают вид:

ф 1 + А ф 2 + ( B₁x + D 1 X 3 - E 1 X 4 + P 1 x 1 - G 1 x ₂ + H 1 x 3 - K 1 x 4 +

R ²

+ N 1 )( R sin ф 1 - —sm2 ф ₁) = 0

ф ₂ + N₂ ф ₂ - ф 1 - ( P₂X₂ - Q ₂ X 3 + S ₂ X 4 - T₂x 1 + U ₂ x ₂ + V₂x 3 + W₂x 4 +

R ²

+ G 2)( R sin ф1--sm2ф1) = 0, где

A = c²- ; B_x = m ¹; D = (1 + R) m3. ; E = ^b m

J ₂ ¹ J ₁    ¹ L J ₁    ¹ L J ₁

G = (1 — ^b ) ^ЬСп^ ; H = (1 + ^Ь )     ; К =

• ¹         L ₁ L J ₁     ¹ L L ₁ J ₁    ¹

^ p = (1 + ^Ь )(1 — ^b ) ^; P ₂ = m 2 ; 12

₁             L      L ₁ J ₁         J ₂

J²- c р ; N = ( R ^ — d ) ^;

LL ₁ J ₁     ¹      h ₂ ^{0     1} J ₁

—

N 2 = C ; Q 2 = LT m 3- ; 5 2 = (1 + L ¹) m 4 ; T = (i — b ) b' п ; и 2 = (1 + Ь )(i — b ) С р ;

J2 L J2           L J2          L1 L J2           LL

V = b c р; W = (1 + b) bCp ; G = (hL b — d ).

• 2   LL1 J2            L L1 J2    2    h2 02

Уравнения движения масс m ₃ и m ₄ составляем следующим образом. Как видно из рисунка 1, брус батана под действием приложенных сил деформируется. Перемещение массы m ₃ можно записать в виде:

единичные силы направлены вдоль этих перемещений; 53F и 53F2 — соответственно перемещение массы m3 под действием силы F1 = 1 и F2 = 1 (направления сил показаны на рисун ке 1 b). Соответствующая величина 53 находится из геометрических соотношений где

L

5 ₃ = x ₃ + ™ x ₂

^— С ^— "L 1 ) ^x 1 .

Приравнивая (7) и (8) с учетом (5), получим уравнение движения массы m ₃ : ^x 3 ⁺ A 3 ^x 3 ⁺ B 3 ^x 4 ^— D 3 ^x 4 ⁺ E 3 ^x 2 ^{— P} 3 ^x 1 = G 3 ,

L ^{1 5} 3 ^F 1 ^bc np        ⁵ 34 ^m 4

A 3 =--------------; B 3 = ------

⁵ 33 ^m 3 L 1          ⁵ 33 ^m 3

^{(1 +}    ) ^{+ 5} 3 F 1 ^{(1 —} "c") ^c np

P 3 =---- L------------L ¹-----;

⁵ 33 ^m 3

L ₂

b c пр          L

^; D 3 = ⁵ 3 f₂ 7 7---- ^; E 3 = —

² L ⁵ 33 ^m 3

—

5 3 F ₂ (1 — ^b ) C np

L 1        ;

⁵ 33 ^m 3        ’

G 3 = ^{( 5} 3 F ^{+ 5} 3 F ₂⁾⁽71 b o ^— d 1 ) ^np

^{1       2}   h 2           ⁵ 33 ^m 3

Аналогично находим уравнение движения массы m ₄ :

x 4 + H 4 x 4 + К 4 x 3 — M 4 x 3 — N 4 x 2 — P 4 x , = Q 4 ,

где

L — 5f bc, H = ^{1    4 F} 2

⁵ 44 m 4 ^b 1

'       5 m пр-; К = Tm; M 4 = 54 F

⁵ 44 m 4             '

bc

—ⁿ— ; N 4 = ^b 1 ⁵ 44 m 4

(1 + L) — 5 4 f 2 (1 — b) ) c-

⁵ 44 ^m 4

пр

;

P4 =

ь — 5 . ,(1 — b ) c „p

⁵ 44 ^m 4

Q , = ( 5 4 F, + 5 4 F, )( h ¹ b o — d 1 ) Ь пр

^{1       2}    h 2           ⁵ 44 m

Из выражений (1) и (2) имеем:

;x j = ( R sin 0 j x = ( R cos ф 1	R 2 - — Sin 2 ф ! ) ф ! R 2 —— cos2 ф 1) ф 1 + ( R sin ф 1	R 2 — "2Г ^^ 2 ф 1 ) ф 1
5c 2 = ( R sin ф1	R 2 — ”27 sin 2 ф 1 ) ф 1 — ( R cos ф 1 "	R 2 - — СО82 ф 1 )< ф 1 ф 2	— ( R sin ф 1	R 2 — "2 /"^^ 2ф 1 ) ф 2		(14)
x2 = [( R sin ф 1	R 2 — ~2Гsln2 Ф 1) — ( R cos ф 1 —	R 2                 && 1 соз2 ф 1 ) ф 2 ] ф 1	- ( R sin ф 1 -	R 2 - — sm 2 ф 1 ) ф 2 +
+ [( R cos ф 1 —	R 2                     R 2 — cos2 ф 1) + ( R sin ф 1 — —	2 sin2 ф 1) ф 2] ф 1 — 2( R cos ф 1 —		R 2               & & cos2 ф 1 ) ф 1 ф 2 l

После преобразования выражений (6), (9), (11) с учетом (1), (2) и (13) получаем следующую систему нелинейных дифференциальных уравнений второго порядка с переменными коэффициентами [4], описывающих движения масс расчетной схемы механизма при ударе в обе пружины замка:

( . R ² . I

1 + B] R sin ф --sin 2 ф I

1 к ^{1 2 1           1}7

х ф^ + A + P 5 R sin ф 1

к

ф 1 + B 1 • R cos ф 1

R ² • о 1 ^— — 81п2 ф 1 7

• x 4 + ^ U ₅ • R • (1 - cos ф ₁)

R

—

—

к

R ² i( - — cos 2 ф 1 I R sin ф 1

ф 2 + S 5 R sin ф 1 к

1 7

—sin² ф 1 + V 5 >• R sin ф 1

2 l

к

—

. „ L .       R R .

1 + P ₂ R sin ф ₁ — —sin2 ф ₁

•• ф 2 +

к

R

\

—

• ^B 1 ^—

^R I

--sin 2 ф 1 х

2 1            ¹ J

/

R ²

—^sin2 Ф 1 I - x 3 + T ^{R si} n ф 1

^{2 1}          7          ⁵ к

R ²

--sm2 ^

2 l ¹

—

R ²        1

— sin 2 ф I = 0, 2 1            ¹ 7

( R²

1 + B[ R sin ф --sin2 ф₁

1к        1 21      -

R

(

1 + P 2 к

к

R

R ²

R sin ф 1 — —sin 2 ф 1

к

R cos ф ₁ --cos2 ф ₁ ф ₂ R sin ф 1 --sin2 ф ₁ R cos ф ₁--cos2 ф ₁ ) •

к

l

_к

2 l

l

R

P ₂ R cos ф ₁--cos2 ф ₁ + R sin ф 1

^

к

_к

(

+ 2 P ₂ R cos ф 1

к

R

^

х <

1 + P 2

l

к

— cos2 ф ₁ R sin ф 1

l

г

R sin ф 1 к

—

R ²

2 1 sin 2 ^ 1

к

—

^

R

2 R² . . )

—— sin2ф1 ф2

¹           7

к

— ^sin2 ф 1 ф . ф 2 +

2 l

R

Rsin ф ₁--sin2 ф ₁ <ф +

к

2 l

(

х A + A5 • R • sin ф1 к

R ²

---sin 2 ф 2 • 1            ¹

(

R cos ф 1 к

к21 Г

—

R ² l

к

1 + B 1 R sin ф 1 к

1 С

—

R ²

— sin 2 ф

2 l         ¹

•

cos2 ф ₁ • ф ₂ • R sin ф 1

—

к

R ²

2 1 sin 2 ^ 1

х

+ N ₂ + B ₅ •к R • sin ф 1

R ²

---sin 2 ф 2 • 1            ¹

ф 2 ⁺

+

1 + B_x R sin ф к

Г

—

R² ■ . ) 2 2^ 81п2 ф ₁

•

<1 + P2

(_ . R² .

R sin ф 1 ——Sin2 ф 1

_к 21

л

—

R cos ф — к

R ²

cos l

2 Ф 1

х ф ₂ ]• R sin ф к

R

+

—

— ^sin2 ф ₁ • D ₅ + E ₅ >•

21         7

(

R sin ф 1 — к

л

R ²

— sin2ф1 x 4 +

21         7

1 + B R sin ф к

R ²

--sin 2 ф

2 l         ¹

• < 1 + P ₂

(

R sin ф 1 — к

R ²

—sin 2 ф

2 l ¹

л

—

(

R

к

cos ф 1 —

R ²

cos l

2 Ф 1 •

х ф2 ] • R • sin ф1 к

R ²

---sin 2 ф 2 • 1            ¹

к

+

(

1 + B 1 R sin ф 1 к

R ²

^— -^ ™2 ^ф ,

R ²

——cos2 ф ₁) • ф ₂] • ( R sin ф 1 —

+ M 5 • R • (1 — cos ф 1 )

—

a ₃ X ₃ + b₃ x ₃ — c ₃ x 4

-

a 4 X 4 + b ₄ x 4 —

• F5 7

—

G 5 f • R • sin ф 1

—

к

R ²

--sin 2 ф 2 • 1            ¹

к

• X 3 + 7

• <

1 + P2 •

(

R sin ф 1 — к

R ² "^  ^ф

к

— ( R cos ф 1

—

R ²

— sin 2 Ф 1 ) • Ш5 • [ ^R • ^{(1 — cos} Ф 1 )

R ₂

--sin ф + N

2 1          ^{1       5}

( d3 R sin ф

к

-

—

R ²

— sin ф I + K, +

2 l ^{1       5}

cx + d₄ R sin ф к

—

( . R² .       ²

R • sin ф---sin 2ф к 21

R ²       )    .Г™ R .2

—81п2 ф 1 1 ф ₂ ⁺ § 3 ^{R (1} - С08 ф 1 ) - 2^- sin ф 1 = q 3

R ² . . )      .                . R .2

— sm2 ф ₁ ф ₂ + 5 4 R (1 — С0S ф ₁) — —sin² ф 1 = q 4 .

> •

= ⁰

R

2 l

R

2 l

2 l

Начальные условия при t = 0 (получены в работе [1]:

Ф1 = 1,9198 рад x3 = 0,09156517м

Ф 1 = 26,2

с

X₃ = 2,0826885 м

с

ф ₂ = — 0,000758 рад    ф 2 = — 0,210545

с x4 = 0,09166565м    X4 = 2,0608894 м

В заключение отметим, что выведены уравнения движения батанного механизма с учетом упругости звеньев при ударном нагружении как шестимассовой системы с четырьмя степенями свободы. Общее решение полученной системы нелинейных дифференциальных уравнений второго порядка с переменными коэффициентами неизвестно, и, следовательно, для ее решения необходимо воспользоваться численными методами интегрирования на ЭВМ [5]. Результаты решения дифференциальных уравнений движения батанного механизма будут проанализированы в следующей статье.