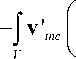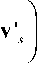Вывод выражений для перекрестной и квадратичной составляющих радиационного давления в случаях идеальной и вязкой жидкостей

В работе [1] для случая идеальной жидкости было показано, что радиационное давление (рд) на включение складывается из перекрестной составляющей рд, вызванной взаимодействием между первичным и рассеянным полями, и квадратичной составляющей, вызванной взаимодействием внутри рассеянного поля. Приведем выражения для соответствующих составляющих рд так, как они представлены в [1]. Для перекрестной составляющей (черта сверху означает временнóе усреднение)

— ( /s )

F

^2

c _ile

= J I - ^P 0 v ™^c ' v s +--- ^P n= ^P s 1 ⁵ ‘k +

^JS ll                   P o           У

+ Onfv' v' +v' v'

ρ 0      nc s_k      s    nc_k

Как следует из [1], квадратичная составляющая равна

F ¹ ‘' -4- p |v' . l² + £ I p ' Г l 6. +

S ll 2        2po

+P Vv'sv's + v'sv7rn dS,  / = 1,3,

0 s     sk        s     skk а в волновой зоне (2), когда S есть поверхность, охватывающей включение сферы, трансформируется к выражению [2]

F(ss )=-1 Po J |v's Г cos y/dS,   / = 1,3.(2а)

2 _S

Это вызвано тем, что в первой скобке подынтегрального выражения в (2) стоит разность средних плотностей кинетической и потенциальной энергий, которые в плоской волне (в волновой зоне), как известно, равны.

Здесь F — проекции векторов рд: s — для перекрестной составляющей, ss — для квадратичной; v ’, _c = ( v', , v \ , v \ ), v \ = ( v \ , v '_s , v \ ) nc          nc ₁       nc ₂ nc ₃           s         s ₁ s ₂ s ₃

— первое приближение колебательной скорости падающей и рассеянной волны соответственно; ρ ₀ — равновесное значение плотности; ρ ' — возмущение плотности первого порядка малости; c — скорость звука в жидкости; S — поверхность произвольного объема, содержащего включение; θ — угол между нормалью к поверхности n = ( n₁, n ₂, n ₃) и i -й осью декартовых координат. Выше и далее для идеальной и вязкой жидкости под характеристиками звукового поля понимаются величины первого порядка малости, т. е. решения линеаризованных уравнений системы Эйлера или Навье—Стокса.

Далее в [1] без вывода дается окончательный вид выражения (1) для вектора перекрестной составляющей рд:

F ⁽⁾ =- P oJ v \nc M' s - -2 -^2 s I d V .       (3)

V l c ^- t У

Здесь ϕ ' — скалярный потенциал скоростей v' = V

v inc ϕ inc , v s ϕ s .

В работе [3] дан конспективный переход от выражения (1) к выражению (3) в тензорном виде. Вызывает, однако, интерес воспроизвести этот переход подробно и в векторном виде, а на его основе получить соответствующее выражение для случая вязкой жидкости.

ПОСТАНОВКА ЗАДАЧИ

В настоящей работе дается подробный вывод выражения (3) в векторном виде из выражения (1) альтернативным приведенному в работе [3] методу. Кроме того, производится полный вывод соответствующего выражения для случая линеаризованной системы Навье—Стокса для вязкой жидкости, аналогичного выражению (3) для линеаризованной системы Эйлера.

РЕШЕНИЕ ПРОБЛЕМЫ

Вначале для решения поставленной выше задачи выпишем линеаризованную систему уравнений Навье—Стокса (см., например, [4–7]), а затем и следующую из нее систему уравнений Эйлера. Рассматриваем для простоты баротропную жидкость. Система состоит из собственно линеаризованного уравнения движения Навье—Стокса

— = -—Vp'+ ^+b VV-v'+ Ц Av',(4)

d t Po        Po линеаризованного уравнения неразрывности

P + PoV-v' = 0(5)

dt и уравнения состояния, связывающего давление p ' с плотностью ρ' :

P' = f (P'), или      P' = c 2 P-

В (4) λ и µ — коэффициенты динамической вязкости (соответственно первый и второй параметры Ламе), связанные с коэффициентами η сдвиговой и ς объемной (второй) вязкости следующим образом:

n = ц,     $ = X + 3ц.

Поскольку линейная задача рассеяния на включении связана с безвихревой (т. е. потенциальной) составляющей скоростей [8], то уравнение (4) для этих составляющих приводится к виду [4]

dv'      1     , X + 2 ц ,

---=--Vp '+-----—Av'.

a t     Po        Po

Из уравнений (5)–(7) при условии равенства нулю коэффициентов динамической вязкости λ и µ немедленно следует система уравнений Эйлера.

Рассмотрение начнем с идеальной жидкости.

Идеальная жидкость

По теореме Гаусса переходим от поверхностного интеграла (1) к объемному. Введем обозначение для тензора T = v^Д + vs v_mCt . Тогда выражение (1) может быть переписано следующим образом

—(is)

F

-4.

V I

f               CI

- Po ^v'inc • v' s⁺—P '.nc Ps ' | ⁺

I              Po        )

+p₀d_k (v_c v\ + v\ v'_mc HdV,  i,k - 1,3.

0 k nc    s_k       s     nc_k

Здесь       d,- —;       p (v ',„ cv \ + v's v \ )- k nc    sk       s     nck d (v' v' +v' v' 1 nc    sk       s     nck

-8 kTk -£ k

5xk

Легко показать, что при преобразовании по- следнего интеграла к векторному виду он записывается следующим образом:

—(is)

F⁽

V

к

-^-jl^V-^Po^{( v}'inc

CI

^-vs ) ⁺ —⁽P mc Ps ) | ⁺

Po          )

⁺Po (⁽v 'inc '^V)v's^{+ (}v 's '^V)v'inc⁺

+ v' V-v' + v' V-v' nc         s s

Учитывая тождество для градиента скалярного произведения двух векторов

V( v ',nc - v's ) = ( v'inc - V) v 's + ( v's - V) v'inc +

+ v 'inc xVx v' s + v ' s xVx v' inc , а также потенциальность колебательных скоростей, получаем

V( v 'inc - v's ) = ( v'inc - V) v's + ( v's - V) v'inc .

С учетом последнего равенства интеграл (8) преобразуется к виду

—(is)

F

f r²

= -f — V(Pinc Ps ) + V к Po

+ Po (vР V- v's + v's V- vP) I d V.

+ Po v 's V- v \nc ) d V =

Далее учтем выражение (7) для линеаризованного уравнения Эйлера (при 1 = ц = 0) и выражение (6), связывающее возмущенные плотность и давление

= - J ( v 'nc /7 's + Po v 'inc V- v's ) d V =

V

= -J v 'inc ( PoV-v 's + P^'s ) d V = V

— V( PP' P s ) ^Х^ Ps '+^ Pinc

ρ₀               ρ₀        ρ₀

Po^Ps - ^PT^'s c

d V =

= - v' P - v' P , nc s s nc , а также линеаризованное уравнение неразрывности (5). Кроме того, очевидно, что для гармонического процесса при интегрировании по периоду колебаний справедливы равенства

-v  P = v P . - v P = v P nc s nc s ,          s nc s nc

(точка сверху означает дифференцирование по времени).

С учетом сказанного получаем цепочку равенств:

= -Po J ^v'inc [^AP 's V V

—

₂ϕ'_s c

| d V.    (12)

Здесь учтено, что v' = V ср' и [P' = —2" Ф. Вы-c²

ражение (12) полностью совпадает с выражением (11) работы [1].

В случае, если бы было принято представление

— V( Pi nc Ps ) = v ' s i 'inc - Po v 'inc V-v ' s , ρ₀

то конечное выражение для рд было бы таким:

c

— ^V(P nc P s ) = ^{- v}inc P s^{- v}s P nc = ρ₀

—(is)

F⁽

- Po J v' s V

nc

--2 Ф me c

d V ^ o.

v'inc ^P's^-Po ^v's V- ^v',

^v's ^Pnc^-Po v'inc ^V- v'

т. к. очевидно, что

- v 's P 'inc = ^v's ^PP = -Po ^v's^{V - v}'inc ;

-^v'inc P ' s = ^v' nc P's = ^-Po ^v'inc^{V - v}' s .

Таким образом, получено два различных представления для первого слагаемого в подынтегральном выражении в (9). Произведем дальнейшие выкладки для варианта

C ------------------- ---------:--- -----------------

— V(PP P's ) = v'nc P's - Po v's V - v'nc .    (1 1)

ρ₀

Подставляя (11) в (9), получаем цепочку равенств:

—(is)

F⁽

= j c^V(P'* P's ) ⁺Po ( v 'nc^V-v's⁺v's^V-v 'nc ) I^{d V} =

VI Po               ^V                    P

= -J ( ^v'nc P's^-Po V's^V-V 'inc⁺Po V 'nc^V-V' s⁺

V

Последнее выражение тождественно равно нулю, т. к. внутри объема V потенциал ϕ' nc удовлетворяет однородному волновому уравнению Ap'nc - -2(p' nnc = o. Дело в том, что в соответствии c с выбранным объемом интегрирования V и охватывающей его поверхности S при получении выражений для рд принимается предположение о том, что источник падающего поля находится вне объема V .

Вязкая жидкость

В этом случае необходимо исходить из линеаризованной системы Навье—Стокса (7), (5), (6). Отличие от идеальной жидкости проявляется только в уравнении движения (7). В качестве альтернативного подхода примем предположение о стационарности процесса с временным фактором e-i“t, который везде далее опускаем.

Приведем здесь соответствующие выражения, связывающие амплитуды характеристик потенциального поля между собой (обозначения для амплитуд оставим теми же, что были для общего случая временнóй зависимости). Из уравнения (7) получаем

1     , 1 + 2 ц _А ,

-i®v' =--Vp ------Av'.

ρ₀        ρ₀

Из соответствующих нестационарных зависимостей [8] получаем для области без источников (особенностей)

С учетом (13) последнее выражение перепишется в виде

Аф'+ к, ф' = 0,                 (13)

Av'+ k,²v' = 0,                   (14)

p " J — ^PL to² к 2 c²

—

, 2 A + 2 ц ) itok, ----— x

' c²J

. p A + 2 ц p = ito-o ф+---2-2- Аф, c2 c2

х(ф ')²— 2 Po (VO ')².

p' = itop_oф+ (A + 2 ц )Аф'.

После подстановки в (19) выражения (15) получаем следующее выражение для p'' :

Последнее выражение легко преобразуется к следующему виду (см. [9]):

iρ c²k²

p' = —⁰—— ф .

ω

Для плотности, учитывая (6), имеем iρ k 2

P = —^o  ф .

ω

1 + p" = ^k—

to²(A + 2 ц )²

Здесь

2 f k,2 = -г 1 - ito

\-1

A + 2ц )

к

Po c²J

k_l²— квадрат волнового числа продольных волн [7].

Далее модифицируем выражения (15), (16):

• Vp' = Poc k v',(15а)

ω

• Vp' = i^k- v'.(16а)

ω

Из уравнения неразрывности (5) получаем

• itoP = PoV • v' = p0 Аф'.(18)

Преобразуем выражение (1) для случая вязкой жидкости при условии, что оценивается составляющая средней силы, вызванная только взаимодействием волн при пренебрежении акустическими течениями, т. е. для случая оценки радиационного давления по терминологии работ [10–12]. Если пренебречь влиянием акустических течений на среднюю силу, то тензор напряжений вязкой жидкости второго порядка малости σ_ik '' может быть принят равным p_k" ~ -p" 5_lk. Здесь p" — величина давления второго порядка малости. В работе [13] без учета акустических течений получено выражение для p '':

p " = "Pc² (-i®Ф ')2 — 2 Po ^Ф'^ + ito^A+2²2^Ц Ф Аф '•

24 ρ0 c

2ρ₀c²

⁽p ')2—2 Po ivI².

С учетом (20) выражение (8) для вязкой жидкости преобразуется к виду

—(is)

F( ) = f                  c2

= - J^{V —}Po^(v' .nc • v ' s ) ^{+ a} — ⁽P 'ncc P ' s ) I d ^V =

V к                  Po

= ^— J( Po^(v' ,nc '^V)v ' s^{+ (}v' s '^V)v' inc⁺

V

+v' inc V^ v' s + v' s V^ v' inc) d V.(21)

О             . ^{to2(A + 2 ц )2}

Здесь a = 1 +-----—4---. Тогда выражение, ана-

ρ₀²c⁴

логичное выражению (9) для идеальной жидкости, в случае вязкой жидкости имеет вид

—(is) г^ с²----------------

F⁽ )= —f a—V(P_ Ps) +

V к  Po

+ Po (v 'inc V • v' s + v' s V • v' inc)) d V.

Далее раскроем первое слагаемое под интегралом в (21). Для этого воспользуемся выражениями (16а) и (18).

c²

^a —^V(Pnc ^Ps ) =

ρ₀

c²

= ^a — ^V(Pinc )^Ps⁺P 'и.^VP's = ρ₀

c² f

=^a— Po к

—J

iρk²

—^-^- v'  P + P inc s inc ω

iρ₀k_l² ω

c²f ■ a —

Po к

^Pok,- v'inc itoP's + itoP V_nc^P0k^- v's ω²                 ω²

c²

^—a — ki' (v 'inc Po ^АФ's⁺Po ^V" v'inc v's ) = ω

—

7   ®²(^X + ²ц)²I c²

1 +                  X

к       P_o²c⁴    J ®²

^Xki² ( v 'inc Po ^Аф's⁺Po^V" v'inc v's ) =

—

1+

к

®²(Х + 2ц)² ] с^ ®²_х

Po c⁴    J ®²c c

X

®²(X + 2 ц )²

• 1    + Л 2^4

к Po c J

X

X 1 +i®

—

к

1+1® к

■ ^( v 'inc Po^A^ s + PoV" v \nc v ' s ) =

X + 2ц ρ₀c²

■ ^(v'inc Po^Афs + Po^V" v'inc v's )

X + 2 ц ρ₀c²

^—Po ( v 'inc^Афs^+V" v' inc v' s ).

На 2-м шаге последовательных эквивалентных преобразований (23) использовано выражение (16а), кроме того, на 3-м шаге заменен знак на противоположный вследствие следующего факта. Пусть A₁ и A₂ — амплитуды стационарных гармонических сигналов A₁ e^—i®t и A2e^—i®t (здесь временно для наглядности возвращен временной фактор e^—i®t). Тогда легко проверить, что имеет место равенство

(—i®A1 e^—i®t) A 2 e^—i®t

= — A e—i®t (—i®A2e—i®t), аналогичное равенствам во временнóй области, приведенным после выражения (10). Кроме того, для двух процессов A1 e—i®t и A2e—i®t имеет место общее равенство для среднего их произведения по 2π периоду T = —:

ω

• A, e^—i®^tA2 e^—i®t =

T

= - J (Ae^-i®t + A * ei®t)(A₂e" i®t + A₂ * ei®t) dt =

T0

= 2Re A1 A2 ’.

На 4-м шаге (23) использовано тождество (18).

На 6-м шаге использован перенос мнимой едини- цы в выражении для kl2 (17) в числитель. На 8-м шаге использован тот факт, что для реализации волнового процесса в вязкой жидкости необходимо выполнение условия [7, с. 23]

X + 2 ц ₁

®----<< 1,

ρ₀c²

, . X + 2ц вследствие чего в выражении 1 +1®----— мни-

ρ₀c²

мой составляющей можно пренебречь.

Подставляем итоговый результат (23) в (22), получаем

F⁽is) = ^— j (^—Po v'inc ^A^'s⁺Po v'inc^V" v 's ) ^dV =

V

= — Po j v'inc (A + ki² >'sdV.                       (24)

V

Здесь по умолчанию реальное включение заменяется точечным, а рассеянное поле во всем объеме V , исключая эту точку, удовлетворяет уравнению Гельмгольца (13), и, следовательно, вне этой точки справедливо равенство Аф'_s =— k_i2ф’_s. Таким образом, мы пришли к исходному выражению для идеальной среды [1, выражение (11)], но для гармонического процесса и в вязкой среде.

Наконец, выражение (24) может быть записано в удобном для вычислений виде, аналогичном полученному ранее для идеальной среды [14, выражение (1)]:

F⁽“) = — P¹J v' nc ((A + ki² )ф' s )* d V + к.с.     (25)

4_V

Исходя из (2) и (20) выражение для квадратичной составляющей рд может быть записано так:

—(ss)

Fi( ’

W

—

П — ^Px ' si

5 Ik ²

a I 12 Ie

⁺W ¹ ps\ ^^Si‘⁺

+ P (^vk vk + vk vk )n fds,  i = 1,3.

0      s_i     s_k s_i     s_k     k

Учитывая, что a ~ 1, последнее выражение для вязкой жидкости записывается идентично выражению (2) для идеальной жидкости:

Fss *-j|7- P1 |v's r+T77I p's r 18» + s Ik 2        2Poc

+ P (v k v k + v k v k ) I nds, i = 1,3,(26)

0      si sk         si skk а в волновой зоне в точности совпадает с выражением (2а) для идеальной среды.

ВЫВОДЫ

Таким образом, в работе приведен подробный вывод полученных ранее выражений для перекрестной и квадратичной составляющих радиационного давления в идеальной среде. Получены выражения для составляющей радиационного давления в вязкой среде, обусловленной взаимодействием первичной и рассеянной волн. Эти выражения оказались по форме совершенно аналогичны выражениям для идеальной среды. Этот факт позволяет экстраполировать всю наработанную для идеальной среды технику на случай вязкой среды в части, касающейся оценки упомянутой составляющей радиационного давления.