Взаимодействие двухсолитонных импульсов в нелинейноm многомодовом волноводе

Существенным недостатком многомодового волокна является наличие уширения импульса в результате групповой и межмодовой дисперсии. В одномодовых волокнах, получивших широкое практическое применение, межмодовая дисперсия отсутствует, а нелинейность показателя преломления волокна позволяет нелинейным сжатием скомпенсировать дисперсионное расплывание импульса [2-4].

В работе [5] для предотвращения уширения импульса за счет межмодовой дисперсии предложено использовать инвариантные модовые пакеты. Другими словами, принципиально возможно построение многоканальной линейной ВОЛС, в которой в качестве носителей отдельных каналов передачи информации будут использованы пакеты мод, имеющих одинаковые значения постоянной распространения. Интерес к поперечным модам как носителям независимых каналов передачи информации связан, во-первых, с постоянным повышением качества производимых многомодовых волокон [11], во-вторых, c разработкой методов качественного синтеза дифракционных оптических элементов - мода-нов [12, 13], способных эффективно формировать и селектировать поперечные моды лазерного излучения. Общая теория построения телекоммуникационных систем с уплотнением каналов в линейной ВОЛС, основанном на использовании поперечных мод, детально изложена в [12].

В связи с появившейся возможностью селективного возбуждения поперечных мод представляет интерес вопрос совместной эволюции импульсов, соответствующих различным модовым пакетам, в нелинейных волноводах.

В [1] проведено численное исследование эволюции амплитудных огибающих односолитонных лазерных импульсов. В данной работе приводятся результаты для двухсолитонных импульсов.

меняющихся амплитуд описывается системой уравнений шредингеровского типа [6,7,8]:

дФ j / дФ ,■     1 „

---j + р / j - i ¹ р '' д z        д t 2 j

дz

д t

д 2Ф j

---^- ^{+ 2 к} 0 « кед * д t²

*( X R jm 1^Ф m l² + 2 jj| О m * j

где суммирование ведется по всем каналируемым модам;

P j - постоянная распространения j -ой моды;

j

к )-1

■e, l¹

----I - групповая скорость j -ой моды; дш J

^{Г д 2} в I^{- 1}

дш 2

V У

- дисперсия групповой скорости;

да да                              2

J J Um (x, У)| Uj (x, У)| n0(x, У)dxdy p _ -да -да______________________________________

R^mj =             да да

J J U m ^{( x} , У )| dx^

-да -да

;

U j ( x , y )- поперечное распределение поля j -ой

2 п моды; к =--волновое число;

Г ⁿ 0^{( x} , У ) = n ¹ -А

( 2

x + y

V V

R ²

-

распределение ли-

нейного коэффициента показателя преломле-ния в параболическом волокне.

В данной работе рассматривается случай распространения двух инвариантных модовых пакетов, состоящих из мод Гаусса-Эрмита с индексами (p, q) и (q, p). Представим импульсы в каждой моде в виде:

^ n ⁽ x , У , z , ^t ) = U n ⁽ x , У ^)ф n ⁽ z , ^{t ) e}

,

2. Теория распространения мод в нелинейном волноводе

Эволюция амплитудной огибающей Ф j ( z , t ) j -ой моды многомодового оптического волокна во втором приближении теории дисперсии, при пренебрежении затуханием, зависимостью групповой скорости от интенсивности, нелинейным поглощением и другими факторами в приближении медленно-

n = 1,4;

n = 1 и n = 2 первый модовый пакет;

n = 3 и n = 4 второй модовый пакет.

Совместная эволюция амплитудных огибающих четырех мод в нелинейном волноводе описывается системой:

^^{Ф п} + р ^дФ n- - i ¹ р // ^Ф^ + д z nⁿ д t 2 n д t ²

z 4           2    1           2

^{+ 2 i K} 0 ^пнел ⁽ ^ R nm |^Ф m | ⁺ ~^^Rnn |^Ф n | ^)Ф n = ⁰ , m = 1             ²

m ^ n

n = 1,4.

Наложим следующее условие: на входе в волокно амплитудные огибающие мод одного пакета имеют одинаковый вид ( Ф 1 (0, t ) = Ф 2 (0, t ), Ф 3 (0, t ) = = Ф 4 (0, t )), что эквивалентно случаю одновременного возбуждения мод пакета. Используя данное условие и то обстоятельство, что в 1 = в 2 , @ 1 = ^в 2 , Э \ = Pl , R 11 = R 22 , R 12 = R 21 , R 13 = R 24 , R 14 = R 23 , уравнения, описывающие эволюцию первой и второй моды, идентичны. Аналогично - для третьей и четвертой моды. Таким образом, в данной постановке задачи, достаточно рассмотреть систему из двух эволюционных уравнений, для огибающей первого модового пакета и второго. Далее индексом ‘1’ будем идентифицировать величины, относящиеся к первому модовому пакету, а индексом ‘2’ — ко второму.

В нормированной сопровождающей системе координат с02 п =    z,

Л

Импульсы называются односолитонными, если Ф о j = 1, и N -солитонными, если Ф0 j = N , где N >  2 . Из системы (4) видно, что для получения N -солитонного импульса в первом модовом пакете необходимо <Е> 01 = N , а во втором модовом пакете

~

^{- Ф} 02

= N

кш \ K 22

2. Результаты численного исследования распространения двухсолитонных модовых пакетов

Решение системы (4) производилось разностным методом, предложенным в работе [9] для решения систем уравнений Шредингеровского типа.

Исследование проводилось для следующих значений: длина волны излучения Л = 1,55 - 10 - 6 м ,

n = 1,458, А = 0,009, значение нелинейного коэф

фициента        показателя nHeд= 1,2■ 10 221-| . Для нел

преломления различных экспери

ментов меняли только радиус волокна R .

Важной особенностью N -солитонных импульсов является их периодичность по п [10]. Величина

т = -1С t

- z

^т 0

к

|

,

Ф = У ^нел K ¹¹ _{Ф ;}

J         C 0

эволюционные уравнения принимают вид: ~      ~~

. дФ 1 . дФ 1    1 д ² Ф 1

i--+ iq1--1~—+

дп       дт 2 дт2

периода, выраженная в дисперсионных длинах L g = т о J|д ^/Z|, равна П 2 . Пример такого периодического изменения формы огибающей показан на Рис.1.

+

~

+ 2 K 2 ^K 11 ~

Ф1 = 0

дФ i----+ iq 2----+ —а

дп дт 2

дФ 2

~ д2Ф дт22 +

,

+ С 2 ^ |^Ф1| к K 11 ^{1 1}

1²₊ K 22

^K 11

~

|ф 2 = 0

где введены следующие обозначения:

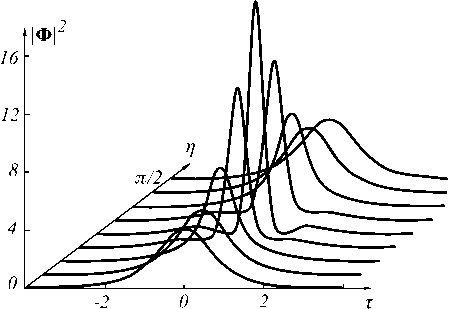
Рис.1. Эволюция амплитудной огибающей двухсолитонного импульса в нелинейном волокне

qi =

^^^^^^в

л в/ - в/            в/ г    q2 = -qb а = Р-’ в1 21 0                    в1

K 11 = R 11 ^{+ 2} R 12 , K 12 = R 13 ⁺ R 14 , K 21 = R 31 + R 32 , K 22 = R 33 + 2 R 34 .

Пусть ^т 0 =

C 0

- длительность импульса .

Начальные условия для системы (4) подставлялись в виде

~

~

Ф j (0, т ) = Ф o j sech( т ) (5)

При одновременном возбуждении двух модовых пакетов с разными групповыми скоростями распространения возможно несколько вариантов эволюции в зависимости от выбранного радиуса волновода.

Первый вариант: модовые пакеты расходятся (Рис.2). На начальном этапе импульс в каждой моде эволюционирует как в случае отсутствия межмодового взаимодействия, но заметны некоторые отличия у передних и задних фронтов импульса. По мере

распространения от переднего фронта импульса “быстрого” модового пакета отщепляется небольшой по амплитуде импульс; аналогичное явление происходит для заднего фронта импульса “медленного” модового пакета. При дальнейшем распространении, отщепившийся импульс распространяется со скоростью большей, чем у основного импульса, и близкой к скорости в случае отсутствия межмодового взаимодействия (рис. 2, пунктирная линия). После расщепления, каждый импульс стабилизируется к форме односолитонного импульса.

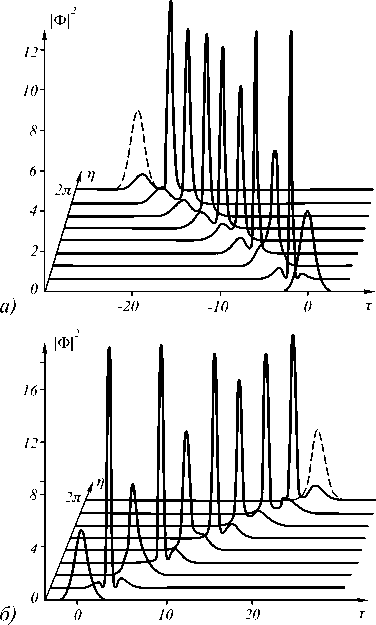
Рис. 2. Эволюция двухсолитонных импульсов в случае одновременного воздуждения двух модовых пакетов (0,1) и (0,2) в нелинейном параболическом волокне. Случай расхождения. R=30 мкм. Пунктиром показан импульс в случае отсутствия межмодового взаимодействия: а) модовый пакет (0,1); б) модовый пакет (0,2)

Второй вариант: в результате взаимодействия импульсов на входе в волокно каждый из них расщепляется на три импульса, причем два из них распространяются в направлении, соответствующем данному модовому пакету (во введенных координатах), а третий — в противоположном направлении. Скорость распространения импульсов значительно отличается от скорости в случае отсутствия межмодового взаимодействия. Форма импульсов приближается к форме односолитонного импульса рис. 3.

Заключение

Полученные результаты показывают существование различных вариантов эволюции амплитудных огибающих двухсолитонных импульсов в нелинейном многомодовом волокне, зависящих (в предложенной системе координат ) от скорости расходимости импульсов. Наличие межмодового взаимодействия на входе в волокно приводит к распаду первоначального двухсолитонного импульса в каждой моде на несколько односолитонных импульсов, с различной длительностью и интенсивностью. Также происходит изменение скорости распростра-

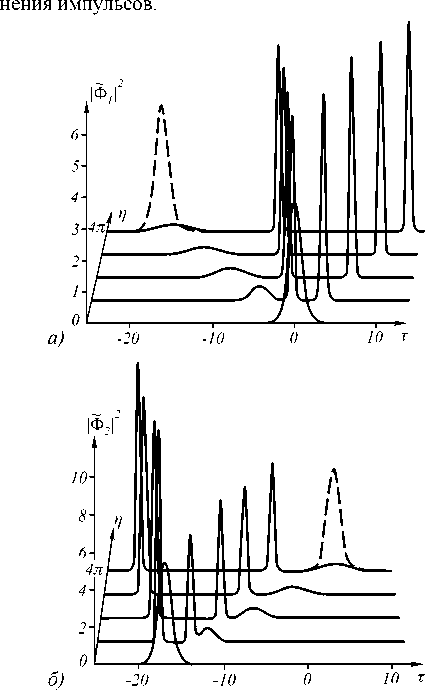
Рис. 3. Эволюция двухсолитонных импульсов в случае одновременного возбуждения двух модовых пакетов (0,1) и (0,2) в нелинейном параболическом волокне. Случай расщепления. R=73 мкм. Пунктиром показан импульс в случае отсутствия межмодового взаимодействия: а) модовый пакет (0,1); б) модовый пакет (0,2)

Наличие данных эффектов потребует своего учета при проектировании многоканальных ВОЛС. Исследованные эффекты также можно использовать для получения односолитонных импульсов из двухсолитонных. Аналогичные результаты распада первоначального импульса нами были получены для трех- и четырехсолитонных импульсов.