Взаимодействие энергии продуктов взрыва, скважинообразователя и грунта в системе взрывофугасного грунтовытеснения скважин в основаниях набивных свай

Раскрытие сущности механического взаимодействия элементов системы «машина-грунт» в рабочем процессе даёт возможность выбора правильного подхода к проектированию взрывофу-гасно грунтовытесняющих скважинообразовате-лей. С этой целью система, состоящая из корпуса, фугасника и грунта, анализируется с позиций статики, динамики и кинематики [1, 2]. Применительно к настоящей работе:

• -    в статике определяются активные силы, связи между материальными точками, реакции связей или пассивные силы и равновесие системы;

• -    в динамике рассматриваются прямолинейное движение материальных точек и силы в качестве причины поступательного движения;

• -    в кинематике исследуются законы прямолинейного поступательного движения материальных точек без отражения причин движения, при этом искомыми величинами являются путь, скорость и ускорение.

Статика корпуса, фугасника и грунта

В работе применяется взрывофугасный грунтовытесняющий скважинообразователь СВГ-216/840. Его принципиальная материальная схема изображается на рис. 1, а. На схеме в качестве материальных тел представлены фугасник 1, корпус 2 и грунт 3. Тела условно принимаются за материальные точки с сосредоточенными массами, соответственно, m1, m2, к этим массам приложены активные силы тяжести Р1 и Р2, направленные вертикально вниз. При установке машины-скважинообразователя в исходное положение на дневной поверхности грунта 3 посредством связи наконечника, опирающегося на грунт, в грунте генерируется реакция связи, или пассивная сила N направленная вертикально вверх. При грунтовы-теснении скважины 4 связь между машиной и грунтом осуществляется через наконечник камуф-летника 5, газы взрыва 6 и головную часть оживальной формы фугасника 1. Схема сил, действующих в статике, представлена на рис. 1, б.

Условие статического равновесия системы взаимодействующих материальных точек

N ^ R c ,                                   (1)

где N - реакция грунта на силу тяжести машины; R_c - предельное статическое сопротивление грунта вдавливающему засилению фугасника.

Реакция грунта на силу тяжести машины

N = P + P 2 .                              (2)

При воздействии силы импульса взрыва F в камере взрывания условия статического состояния рассматриваются отдельно для корпуса и фугасни-ка с грунтом. Статическое состояние корпуса сохраняется до момента достижения силой импульса взрыва значения силы тяжести корпуса, что описывается равенством:

F i = P 2 ,                                       (3)

где F - значение возрастающего давления импульса силы взрыва в камере взрывания.

Состояние покоя фугасника с грунтом определяется зависимостью:

• F + 71 + P , = R c .                            (4)

Таким образом, активные силы, связи, реакции и условия равновесного состояния системы материальных точек машины и грунта определены.

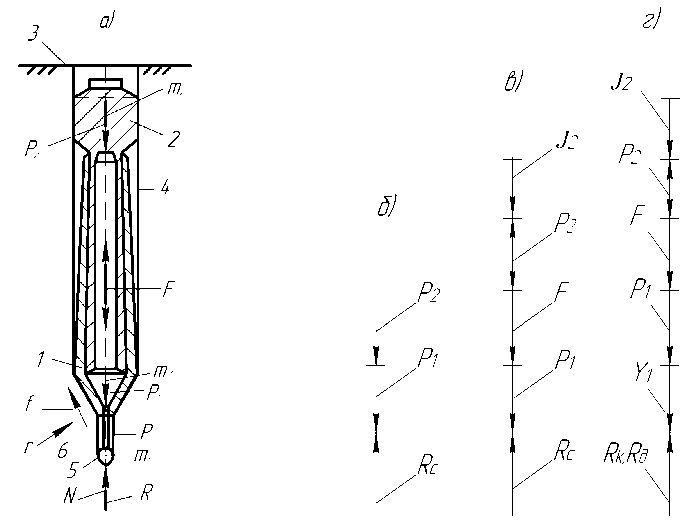
Рис. 1. Схемы: а - принципиальная материальная грунтовытесняющей машины;

б, в, г - силовые, соответственно, в статике, динамике корпуса, кинематике машины и грунта

Динамика системыскважинообразователя и грунта

В процессе приложения импульса силы взрыва F в камере взрывания статическое состояние корпуса сохраняется до момента достижения силой значения, равного силе Р ₂. В следующий граничный момент времени действия силы F_i корпус переходит в движение. В соответствии с началом Д'Аламбера в каждый момент времени силы, приложенные к материальной точке, уравновешиваются силами инерции. В этой системе проявляется сила инерции корпуса J ₂ . Это кажущаяся сила, возникающая как следствие ускорения. Причиной ускорения являются активные силы. Во взаимодействии силы инерции и активные силы обеспечивают динамическое равновесие. Динамическая схема сил, действующих на корпус, изображается на рис. 1, в. Взаимодействие сил описывается следующим уравнением:

P 1 + P₂ + J 2 - F + F - R c = 0.              (5)

Фугасник, опирающийся на грунт, сохраняет статическое состояние до момента достижения нагрузки, равной сопротивлению грунта R_c . При соблюдении условия

P + P 2 + J 1 >  R c                          (6)

фугасник с присоединённым грунтом переходит в движение. В это время возникают силы инерции фугасника J1 и грунта J3 . Грунт приобретает ква-зистатическое сопротивление Rк , которое перерастает до предела условного динамического по мере роста силы импульса взрыва F . Квазистати-ческое сопротивление грунта обеспечивается трением f и распорным давлением R по боковой по- верхности наконечника камуфлетника и головной части оживальной формы фугасника, реактивным давлением газов взрыва P, истекающих в грунт, и силы инерции массы грунта J3 , перемещаемого при физическом засилении фугасника в него, моделируемого сосредоточенной массой m3, присоединённой к острию фугасника. Квазистатическое сопротивление грунта взрывофугасному засиле-нию фугасника является пассивной силой и выражается равенством:

R к = F ( f + r + P ) + J 3 ,                  (7)

где F ₀ – рабочая площадь боковой поверхности наконечника камуфлетника и головной части оживальной формы фугасника. Квазистатическая и динамическая схемы сил, действующих на машину и на грунт, изображаются на рис. 1, г. Их взаимодействия выражаются следующими равенствами:

• -    квазистатического сопротивления

P1 + P2 + J2 + F - F - J1 - Rк = 0;(8)

• -    динамического сопротивления

P + P2 + J2 + F - F - J1 - Rд = 0.(9)

Силы инерции направлены в сторону, противоположную ускорению тела, и определяются по формуле:

J = ma ,(10)

где m - масса тела; a - ускорение движения тела.

Рассматривается график изменения удельного квазистатического давления газов взрыва в камере. Из этого графика выделяется та часть давления, от которого совершается рабочий ход фугасника и газов взрыва. Это давление ограничивается значениями f _н, f ₁₀ и f _к. Выделенное давление изображается линейным графиком зависимости на рис. 2.

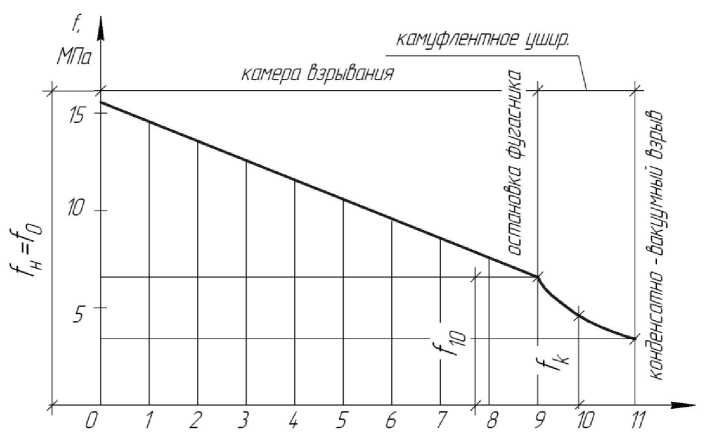
Рис. 2. График изменения удельного давления в процессе рабочего хода фугасника и газов взрыва в камуфлетной полости

Глубина засиления фугасника в грунт по оси абсцисс в пределах давлений f _н и f ₁₀ разбивается на промежутки. По графику в точках разбивки берутся удельные давления f_i . В точке 10 фугасник останавливается при равенстве импульса взрыва в камере и в камуфлетной полости. Равенство имеет следующий вид:

f i0 S р.п = f к S ф ,                              (11)

где S _р.п – площадь поперечного сечения рабочей полости фугасника; S _ф – площадь рабочего сечения фугасника (формователя скважины).

Мгновенные значения импульса силы газов взрыва

F = fS п.ф ,                              (12)

где S _п ф - площадь поперечного сечения рабочей полости фугасника.

Мгновенные значения силы инерции для фу-гасника и корпуса, соответственно,

J i = F + p i + R _д;                         (13)

J i = F - P 2 .                               (14)

Следует рассмотреть перемещение корпуса под действием импульса силы взрыва вверх или его отдачу. С отдачей связана непроизводительная потеря проектного продольного хода фугасника при физическом засилении его в грунт. Чтобы сообщить телу ускорение и обеспечить его движение с определённой скоростью, необходимо совершить работу. Сила, производящая работу с фугасником и с корпусом, соответственно

F =      ;(15)

m ₁

F2 = Fm-.(16)

m ₂

Уравнение динамического равновесия

P2 - F2 + J2 + F - J, + Px - Rд = 0.(17)

В случае состояния покоя корпуса сила инерции J ₂ = 0, а уравнение (17) преобразуется в следующий вид:

P2 = F2 + Rд - Px = 0.(18)

Равенство (18) является условием сохранения состояния покоя корпуса в системе, на основании которого делается заключение о том, что сила тяжести корпуса должна быть равна или больше действующей на корпус силы взрыва, пропорциональной массе фугасника, и силы динамического сопротивления грунта засилению фугасника, за вычетом силы тяжести фугасника.

Кинематика фугасника и корпуса в грунте

Кинематика машины и грунта рассматривается на примере движения фугасника, которое является прямолинейным: в начале пути неравномерно ускоренным, а затем неравномерно замедленным. Соблюдение условия отсутствия отдачи корпуса обусловливает его применение материалоёмким и громоздким, что во многом при эксплуатации является нежелательным. Следовательно, с целью уменьшения массы корпуса имеется необходи- мость допущения оптимального значения отдачи корпуса.

Мгновенные ускорения прямолинейного движения фугасника выражаются из уравнений (10) и (14) соотношением:

a i =

^Fi + P i - R g

m ₁

Средние ускорения a n = ⁰ , ⁵ ( a i + a i + 1 ) ,

где a i - мгновенное ускорение в данной точке;

a i + 1 - мгновенное ускорение в последующей смежной точке данного промежутка пути.

Время движения по каждому отрезку пути

Г 2 S" Г5

n tnI I

V a n )

.

Приращение скорости по каждому участку пути

AVn = antn .(22)

Скорость движения по отрезкам пути рассчитывается как слева, так и справа

Vn = Vn-1 + antn .(23)

Время движения по интервалам пути tn = ^Tn .(24)

Vn

По полученным значениям скорости и времени движения строится график их зависимости, который представляется на рис. 3. По графику определяется область экстремума, т. е. момента перехода фугасника с ускоренного движения на замедленное. Путь, пройденный фугасником:

S n = 0,5 ( V n - 1 + V n ) t n .                      (25)

Поскольку на фугасник действует переменная сила газов взрыва, то общий закон движения можно найти путём решения задач математической физики. Частные решения при конкретных начальных условиях получаются с помощью численных методов. Среднее ускорение в течение некоторого промежуточного времени

V -V 1

n ^r n - 1

a n =--------- .                                ⁽²⁶⁾

A t

При условии, что среднее ускорение мало отличается от мгновенного в конечный момент времени t = t_n , значение средней скорости

V n = V n - 1 + a n a t .                            (27)

Средняя скорость движения за данный промежуток времени числено равняется отношению перемещения к промежутку времени

V = A S = S n - S n - 1 ⁿ    A t       A t '

Из уравнения (28) перемещение

S = S n - 1 + V n A t .

Равенство (29) является законом

(29) движения

фугасника. Строится экспериментальный график зависимости «время–путь» S = f ( t ). График изображается на рис. 4. Путь прохождения фугасника определяется по формуле (25).

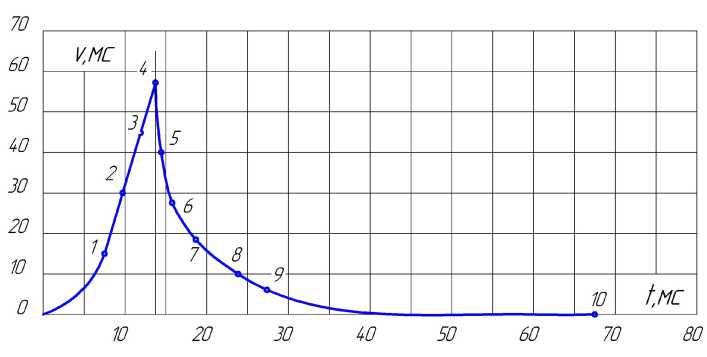
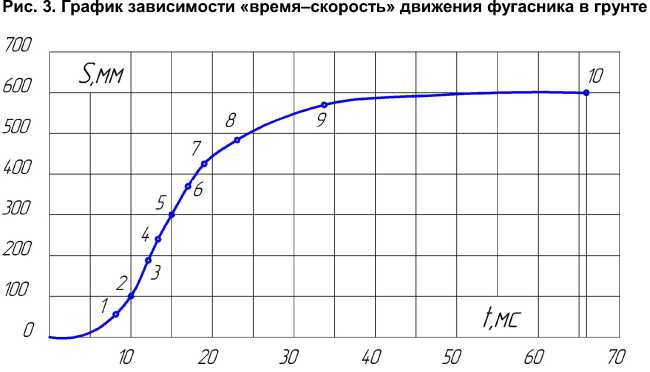
Рис. 4. График зависимости «время–путь» движения фугасника в грунте

Движение корпуса рассчитывается по методике определения движения фугасника с некоторыми дополнениями. Дополнения обусловлены продолжением движения корпуса после точки 10 при расширении камуфлетной полости до точки 11, в которой происходит конденсатновакуумный взрыв. По результатам примера расчета на рис. 5 построен график зависимости «время– скорость», на рис. 6 - расчётный и экспериментальный графики зависимости «время–путь» движения корпуса.

Анализ графиков «время–путь» движения корпуса показывает следующее:

• -    до достижения силой импульса взрыва в интервале точек 8–9 значения, равного динамическому сопротивлению грунта, отдача корпуса составляет 25 мм; при конденсатно-вакуумном взрыве в точке 11 - 153 мм;

• -    включение грунтовых анкеров в работу останавливает движение корпуса, при этом сила сопротивления анкеров превосходит силу сопротивления взрывофугасному вытеснению грунта;

• -    если оснастить взрывную камеру выпускными окнами газов взрыва и снижать давление выпуском газов до атмосферного при рабочем ходе в интервале точек 8–9, равном 510 мм, то потеряется 90 мм пройденного фугасником пути, однако при этом отдача корпуса составит всего 20–30 мм, а масса корпуса может быть уменьшена до 30 % по сравнению с расчётной при нулевой отдаче корпуса.

Выводы

• 1.    Впервые теоретически, экспериментально и практически проанализирована система взрывофугасного скважинообразователя, состоящая из корпуса, фугасника и грунта с позиций статики, динамики и кинематики.

• 2.    Статическое состояние корпуса сохраняется до момента достижений силой импульса взрыва значения силы его тяжести, а фугасника – с момента достижения силой импульса взрыва величины силы сопротивления грунта его внедрению.

• 3.    Сила тяжести корпуса должна быть равной или больше действующей на корпус силы взрыва,

  

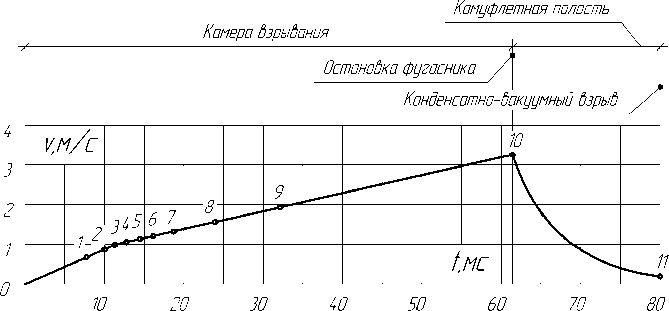
  Рис. 5. График зависимости «время–скорость» движения корпуса

  
  
  

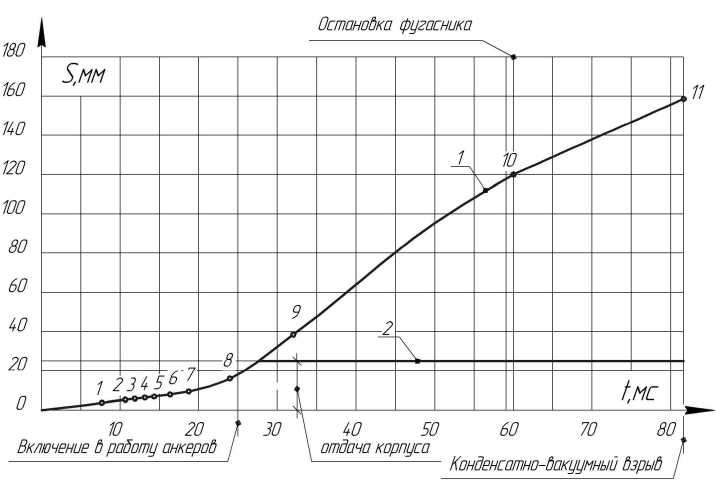
  Рис. 6. Графики зависимости «время–путь» движения корпуса: 1 – расчётный; 2 – экспериментальный

  
  

• 4.    При уменьшении силы тяжести корпуса по отношению к равнодействующему значению силы импульса взрыва пропорционально увеличивается величина отдачи корпуса, на значение которой уменьшается производительный ход фугасника, однако при этом масса корпуса может быть уменьшена до 30 % по сравнению с расчетной при нулевой отдаче корпуса, что значительно снижает металлоемкость и громоздкость корпуса.

пропорциональной массе фугасника и силы динамического сопротивления грунта засилению фу-гасника, за вычетом силы тяжести фугасника.