Взаимодействие поверхностных акустических волн с адсорбированной водой на поверхности ниобата лития

Упругие возмущения, распространяющиеся вдоль плоской свободной границы изотропного или анизотропного твердого тела, смещения в которых аналогичны смещениям в рэлеевской волне, принято называть поверхностными акустическими волнами рэлеевского типа (ПАВ). Формирование граничного слоя при адсорбции пара или другие явления на поверхности твердого тела приводят к изменению упругих характеристик приповерхностной решетки и соответствующему изменению параметров упругих волн, поэтому ПАВ можно применять как инструмент для изучения поверхностных процессов [1]. Наиболее просто поверхностные волны возбуждаются и регистрируются в пьезоэлектрических кристаллах, упругие волны в которых сопровождаются электрическими полями [2]. Посредством этих полей ПАВ могут взаимодействовать со свободными или связанными электронами в граничных слоях и тонких пленках, сформированных на поверхности пьезоэлектрического звукопровода.

Под воздействием поля поверхностных сил, возникающих в зоне контакта жидкой и твердой фазы, в жидкости образуется граничный слой с измененной, в отличие от объемной жидкости, структурой. Структурирующее воздействие наиболее заметно проявляется при взаимодействии лиофильных поверхностей с полярными жидкостями [3]. Жидкие прослойки между двумя твердыми фазами, смачивающие и адсорбционные пленки полярных жидкостей называются граничными слоями [4]. Настоящая работа посвящена изучению взаимодействия поверхностных акустических волн с адсорбционными слоями и развитию метода исследования диэлектрических характеристик жидкости в граничной фазе.

Энергия упругой волны сосредоточена в тонком, порядка длины волны слое твердого тела. Электромагнитное поле, сопровождающее упругую волну, проникает в граничащую с поверхностью, диэлектрическую среду также на расстояние порядка длины поверхностной волны. При взаимодействии твердого тела с граничными слоями жидкости происходит возмущение условий распространения ПАВ. Это приводит к изменению амплитуды и скорости волн. Связь параметров ПАВ с толщиной слоя жидкости описывается соответствующими дисперсионными уравнениями [1, 5].

ε f

ε p

p / p s

ρ f , v f

ρ s ,

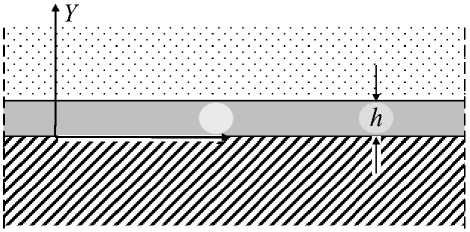
Рис. 1. Слоистая структура «пьезоэлектрик – жидкий слой –

Малое значение толщины слоя жидкости h по сравнению с длиной волны λ позволяет применить метод возмущений. Полагая, что при ( h << λ) в аддитивном приближении влияние слоя жидкости на параметры ПАВ сводится к возмущениям механических A и электрических B условий распространения волны, получим простое выражение, связывающее относительное изменение скорости ПАВ с толщиной слоя:

- ^{∆ v} = ( A + B ) ^h .                                      (1)

v λ

Чтобы найти соответствующие коэффициенты линейного приближения, воспользуемся двумя разновидностями дисперсионных уравнений, описывающих взаимодействие ПАВ со слоем жидкости. В первом случае жидкий слой сформирован на изотропной подложке, не обладающей пьезоэлектрическими свойствами. Во втором – на поверхности пьезоэлектрической подложки. Поверхностные акустические волны в жидком слое на изотропном твердом полупространстве (рис. 1) описываются дисперсионным уравнением [5]:

4 k ² qs - ( k ² + s ²)² = ^{ρ f} ⋅ ^{q t} ⋅ tg( Ph ) ,                           (2)

ρs   P где q2 = k2 - kl2 , s2 = k2 - kt2 , P2 = k2f - k2 , kf = ω/vf , (vf – скорость звука в жидкости). Здесь k, kℓ, kt, kf – волновые числа соответственно рэлеевских, продольных, поперечных волн и волн в жидкости, ρf, ρs – плотность жидкости и твердого тела, h – толщина слоя.

Полагая малым возмущение, вносимое тонким слоем ( h << λ) в уравнение для рэлеевской волны для коэффициента A , получим выражение:

A =

ρ f v f ρ _s v _s

⋅ tg θ _R ,

где θ _R = arcos (ν_f/ν_s) – угол, под которым звуковые волны распространяются в жидкости, ν_s – скорость поверхностной волны.

Следовательно, величина относительного изменения скорости (изотропный случай) определяет- ся акустическими импедансами в жидком слое и твердом полупространстве и волновой утечкой, су- ществующей в такой слоистой системе.

Дисперсионное уравнение, учитывающее электрические параметры слоя, для ПАВ малой ампли- туды, распространяющихся по акустически свободной поверхности, может быть получено с использованием метода электромагнитного импеданса [1]

k - k _{∞ = ε} ε _f th ( kh ) + ε ₀ ^p k - k ₀ ^f ε _f + ε ₀ th ( kh )

Левая часть уравнения – эффективная диэлектрическая проницаемость твердого пьезоэлектрического полупространства с механически свободной поверхностью. Здесь ε p = (ε yy ε zz – ε yz ² ) ^{1/ 2} – диэлектрическая проницаемость, выраженная через соответствующие компоненты тензора диэлектрической проницаемости пьезоэлектрика, k ₀ è k _∞ – волновые числа рэлеевских волн в случаях “закороченной”

и “открытой” поверхности пьезоэлектрика. Правая часть уравнения представляет собой эффективную диэлектрическую проницаемость верхнего полупространства, включая слой жидкости (ε f и ε₀ – относительные диэлектрические проницаемости жидкости и окружающей среды).

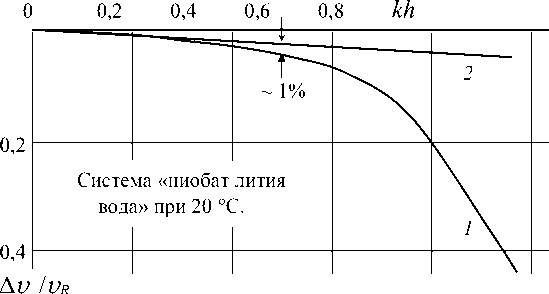
Рис. 2. Зависимость фазовой скорости поверхностных акустических волн от относительной толщины жидкого слоя. р _s = 4640 ³ кг/м ³ ; vr = 3484 м/с; v _l = 7150 м/c; v t = 3751 м/c; v „ = 3484 м/c; £ p

= 50,2; vr = v o ; р f = 998,2 кг/м ³ ; v f = 1483 м/с

Используя условие малости толщины слоя (kh << 1) из уравнения (4), для коэффициента B полу чим выражение:

B

K ^{2 е} p е _f ⋅

²     ( е p + е о )

2 А е —0 Р 2 ^{е f} )

где K - коэффициент электромеханической связи ( K ² /2 = ( к о — к _го ) / к о ).

Численные решения уравнений (2), (4) сравнивали с приближенными вычислениями по уравнению (1) для различных жидкостей и пьезоэлектрических подложек. Зависимость фазовой скорости поверхностных волн от относительной толщины слоя для системы «вода - ниобат лития ( YZ -срез)» представлена на рис. 2. Точному решению соответствует кривая 1 . Кривая 2 соответствует линейному приближению. Вклад в изменение скорости ПАВ механического и электрического нагружения поверхности ниобата лития YZ -среза слоем воды имеет в обоих случаях сравнимые значения ( A = 0,19468, B = 0,21684) [6].

Приближенное выражение дает приемлемую точность при использовании подложек и граничных слоев с предельно возможными физическими параметрами жидкости и твердого тела. Например, отличие найденных численно из решения системы уравнений для слоистой структуры (вода — ниобат лития) точных значений изменения скорости ПАВ в зависимости от нормализованной толщины слоя h/k и приближенных значений, вычисленных по уравнению (1), не превышает 0,01% при h/k < 0,02.

Частотная зависимость комплексной диэлектрической проницаемости диэлектрика с полярными молекулами, в частности воды и льда, в области частот, соответствующих ориентационной релаксации Дебая, может быть представлена уравнением [7]:

ε f

= ε ′ + jε′′ = ε

ε -ε

+——-,

1 + j toT

где £‘ и е"- действительная и мнимая части комплексной диэлектрической проницаемости £f; £s, е„ - соответственно низко - и высокочастотный предел области дисперсии; ю - круговая частота; т - время релаксации.

При малых значениях толщины жидкого слоя, когда справедливо линейное приближение, действительная и мнимая части комплексной диэлектрической проницаемости жидкости в слое связаны с затуханием а и изменением скорости A v поверхностных акустических волн (ПАВ) выражениями:

е ,= 2( е p + I) 2 f a v K 2 е        h to p V „„ = 2( е p + 1) 2 f 2 a v 2 K 2 е p        h to 2 p V

I            2 p f        v 7 - 2 4. / - v f ) ’                             (7) p v f a f —           A f f / 2 ,                                   (8) np s to V1 — v f / v s )

где а f - коэффициент ослабления звука в жидкости, учитывающий потери на вязкое трение (в воде а f / f ² = 25 - 10 ^-17 с ² /см).

Как известно, давление насыщающих паров зависит от температуры и, задавая различные температуры твердого тела и жидкости в объеме, можно получить необходимое давление паров у поверх- ности твердого тела. Различное относительное давление паров p/ps определялось регулируемой двумя термостатами разницей температур подложки (YZ-ниобат лития) и объема воды.

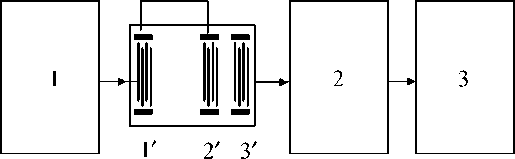
Рис. 3. Блок-схема установки для измерения скорости поверхностных акустических волн.

1 – генератор, 2 – усилитель, 3 – осциллограф, 1 ′ , 2 ′ , 3 ′ – встречно-штыревые преобразователи.

Экспериментально исследовалось взаимодействие ПАВ с водой, адсорбированной на поверхности пьезоэлектрической подложки – звукопровода. Кристалл ниобата лития с оптически полированной рабочей поверхностью YZ -среза предварительно очищался в тлеющем разряде и помещался над поверхностью дважды дистиллированной воды в замкнутый термостатированный объем. Необходимое давление паров p/p_s задавалось и контролировалось с точностью 0,1% изменением температуры подложки ( YZ -ниобат лития) T 1 и температуры дважды дистиллированной воды T 2 . Диапазон частот ПАВ: 40 - 400 МГц. Адсорбция паров воды осуществлялась на рабочую поверхность кристалла между излучающими преобразователями.

В эксперименте использовался метод определения изменения скорости [8], основанный на интерференции ПАВ, возбуждаемых одновременно двумя излучающими и регистрируемых третьим приемным преобразователями (рис. 3). Частоту электрического сигнала, подаваемого на излучающие преобразователи 1 ′ и 2 ′ , настраивают таким образом, чтобы на приемном преобразователе регистрировался сигнал минимальной амплитуды. Это возможно в случае, когда волна, возбуждаемая первым преобразователем, достигая второго преобразователя, интерферирует с излучаемой им противофазной волной.

При помощи метода измерения малых изменений скорости и затухания ПАВ [8] были получены изотермы Δ v/v ( p / p_s ). Как видно (рис. 4), во влажной среде скорость ПАВ уменьшается, причем изменение скорости ПАВ от давления пара носит нелинейный характер и растет с увеличением частоты. Используемый метод позволяет уверенно регистрировать изотерму Δ v/v ( p / p s ) даже при малых значениях

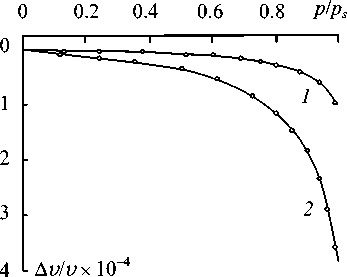
Рис. 4. Зависимость изменения скорости ПАВ от давления пара. 1 – 43 МГц, 2 – 388 МГц.

относительного давления паров. Характер кривых свидетельствует о зависимости параметров адсорбированной воды ( ρ f , v _f , ε f ) от толщины слоя. Необходимо отметить, что кривая 2 (рис. 4) не может быть построена простым увеличением значений кривой 1 в ( f 2 / f 1 ) раз. Это указывает на вероятную зависимость параметров ПАВ, следовательно, и коэффициента ( A+B ) уравнения (1) от частоты. При условии p / p s = const наблюдается нарушение линейной зависимости ∆ v / v ( ω ) в области частот соответствующей ориентационной диэлектрической релаксации. Уменьшение частоты релаксации Дебая возможно в результате модификации структуры воды в граничной фазе.

Таким образом, предложено простое аналитическое выражение, которое описывает взаимодейст- вие упругих поверхностных волн в системе «тонкий жидкий слой – пьезоэлектрическая подложка». Полученное выражение позволяет аддитивно учитывать механическую и электрическую нагрузку, возникающую в результате воздействия жидкого слоя на параметры ПАВ. На основе исследования изотермы изменения скорости ПАВ в зависимости от частоты предложен метод исследования диэлектрических характеристик полярных жидкостей в адсорбционном слое. Показано, что акустоэлектронный метод дает возможность определять диэлек- трическую проницаемость и диэлектрические потери в полярных жидкостях, которые при взаимодействии с твердой поверхностью образуют граничные слои. Поверхностные акустические волны являются чувствительным инструментом изучения процесса диэлектрической релаксации в слоистых структурах, образованных тонкими жидкими слоями. Акустоэлектронный метод позволяет исследовать изменение физических свойств (главным образом вязкоупругих и диэлектрических) полярных жидкостей в граничной фазе в зависимости от температуры, угла смачивания и толщины жидкого слоя.

Работа выполнена при финансовой поддержке РФФИ ( проект 08-02-98006, 08-02-98008_ р _ сибирь _ а ).