Взаимодействие света с обобщенным термо-акустическим полем

ПОСТАНОВКА ПРОБЛЕМЫ

В проблемах научного приборостроения часто возникают задачи взаимодействия различных физических полей, когда эффект, дающий необходимую научную или практическую информацию, является результатом их прямого взаимодействия. Широко известны такие пограничные дисциплины, как акустооптика (возмущение оптического поля при наличии стороннего акустического поля), оптоакустика (возникновение акустического поля в оптических полях), магнитная гидродинамика и т. д.

Одной из таких междисциплинарных проблем является задача описания взаимодействия света с акусто-гидродинамическим полем, вызванным наличием в некоторой сплошной среде комбинированного излучения тепла и звука. Как известно, световое поле возмущается при распространении в прозрачной среде при возмущении параметров последней, в частности при возмущении ее плотности. В сплошной среде термодинамические величины, такие как давление, плотность, температура среды и т. д., связаны между собой уравнениями состояния. Поэтому возмущение температурного поля вызывает возмущение связанных с ним других полей, в частности, поля плотностей. При наличии в среде акустического поля в свою очередь изменение поля давления также вызывает возмущение поля плотностей. Когда в обоих случаях указанные возмущения плотности сопоставимы по величине, необходимо учитывать совокупное возмущение поля плотности, для корректной оценки возмущений светового поля.

В настоящей работе в интересах оценки возмущения светового поля рассматривается задача расчета возмущения плотности среды в результате наличия в ней акустического и теплового полей. Возмущение плотности среды происходит как вследствие ее акустического возмущения, т. е. под воздействием возмущения давления в ней, так и под воздействием изменения (возмущения) температуры среды. Это в свою очередь приводит к возмущению плотности, а следовательно, и показателя преломления. В настоящей работе предпринимается попытка подбора математической модели, адекватно описывающей происходящие в этом случае физические процессы.

ФОРМУЛА ЛОРЕНЦА—ЛОРЕНЦА

Формула Лоренца—Лоренца, рассматриваемая ниже, устанавливает зависимость коэффициента преломления среды от некоторых параметров, в частности, от ее плотности.

Вначале приведем некоторые выражения, связывающие плотность прозрачной среды с ее показателем преломления n = c 0 / c , а значит и с ее диэлектрической проницаемостью ε . Здесь c 0 и c — скорость света в вакууме и среде соответственно.

Согласно соотношению Лоренца—Лоренца [1, с. 5]

n² - 1

n ² + 2

4π

= —Na .

Здесь N ₁ — число молекул в 1 см³; a — скаляр, характеризующий поляризуемость молекулы вещества в среде. Для газов эта формула может быть записана в виде

= -Vp + n^v +

;

n -1           +

----= y = const.

ρ

Для воздуха постоянная у равна: Y = = 0.22635 см³/г. Окончательно для воздуха формула Лоренца—Лоренца такова:

— = 0.22635 см3/г.

ρ

Как видно, для газов вообще и для воздуха в частности показатель преломления и плотность среды связаны линейным соотношением. Запишем его для воздуха в каноническом виде n = 0.22635р +1.

– уравнение Навье—Стокса для несжимаемой жидкости [2, с. 73]

— + ( v -V ) v = -— + ^П A v ;     (1а)

d t V } р р

– уравнение неразрывности для сжимаемой жидкости [2, с. 15]

др +div ( р v ) = 0;

– уравнение неразрывности для несжимаемой жидкости [2, с. 27]

div v = 0;

(2а)

– уравнение сохранения энергии для сжимаемой жидкости [2, с. 273]

Пусть плотность вещества записывается в виде р = р0 + р', где р0 — ее равновесное значение, а ρ' — ее возмущение. Тогда, очевидно, возмущенное значение показателя преломления n ' (показатель преломления также может быть записан в виде n = n0 + n', где n0 — равновесное значение) также линейно связано с возмущением плотности, что с учетом равенства n0 = 0.22635р0 +1 дает окончательную зависимость n' = 0.22635р'.

d s

—+v -V s d t

div (KV T) + c, (V - v )2

П  d v   d vk  2 - d v |

+        *- +   k-     3ik      I

2 ( d x_k   d x i   3 d x l )

+

= div ( k V T ) + D (3)

, „                  2a-\ 2 , П ^d V , vvk ² A -I

(величина D = c( divv) +— —- + —- —^kdivv '    2 dxt dx, 3 ik ki называется диссипативной функцией и представляет собой энергию, диссипируемую в виде тепла благодаря вязкости; член div(kVT) есть тепло,

СИСТЕМА УРАВНЕНИЙ БУССИНЕСКА

Как известно, описание акустического и температурного полей в жидкости следует в наиболее общем случае вязкой, сжимаемой, теплопроводящей среды из системы нелинейных уравнений На-вье—Стокса [2–4 и др.]. Кроме того, в своих предыдущих работах автор периодически обращался к близкой тематике [5–11]. Здесь приведем эту систему в редакции работы [2]:

– уравнение Навье—Стокса (уравнение движения) для сжимаемой жидкости1) [2, с. 73]

приносимое в рассматриваемый объем посредством теплопроводности [2, с. 273]);

– уравнение сохранения энергии (теплоперено-са) для несжимаемой жидкости2) [2, с. 277]

(dT I рср I — + v -VT I = div(KVT) + D ;

(3а)

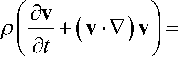
– уравнения состояния; поскольку пять уравнений (1)–(3) для сжимаемой жидкости и (1а)–(3а) для несжимаемой жидкости содержат семь неизвестных ( р , p , v = ( v_x , v y , v_z ) , T и s ), то обычно к ним добавляют два недостающих уравнения термодинамического состояния, например любые два из приведенных ниже (см., например, [2, 4])

p = p ( р , ^s ) , р = р ( p , T ) , ^s = ^s ( p , T ) . (4)

¹⁾ Уравнения (1) и (1а) справедливы в случае, когда изменение коэффициентов вязкости η и ς вдоль жидкости незначительно (что, как правило, имеет место [2, с. 73]) и потому можно считать их постоянными.

В приведенной системе уравнений Навье— Стокса величины p ( x , t ) , v ( x , t ) , p ( x ,t ) , s ( x , t ) и T ( x , t ) это — соответственно поля давления, скорости жидкости, ее плотности, энтропии и поле температур; η , ς — соответственно коэффициенты сдвиговой и объемной вязкости; κ — коэффициент теплопроводности жидкости; s — энтропия единицы массы жидкости; c_p — удельная теплоемкость при постоянном давлении.

Заметим, что для идеальной жидкости система уравнений Навье—Стокса сводится к системе уравнений Эйлера. Уравнения (1), (1а) трансформируются к уравнению Эйлера движения среды:

(dv I

рг^~ + (v’^)v 1 = -^p. (5)

Уравнения неразрывности (2) для сжимаемой жидкости и (2а) для несжимаемой жидкости остаются соответственно неизменными:

^ P +div ( р v ) = 0; (6)

div v = 0. (6а)

Уравнения энергии (3) и (3а) для идеальной среды неактуальны в силу отсутствия в ней потерь.

Уравнение состояния для замыкания системы из четырех уравнений с пятью неизвестными (5), (6) или (5), (6а) требуется только одно, которое вследствие адиабатичности протекающих в этом случае процессов [2, с. 17] сводится к одному уравнению состояния [2, с. 351], [4, с. 10]

Р = Р ( P ) . ⁽⁷⁾

Заметим, что акустическая часть возмущения плотности среды, вызванная акустическим давлением, может быть получена из обычных волновых уравнений линейной акустики, следующих из системы уравнений Эйлера для идеальной среды после их линеаризации (см., например, [2, § 64]).

Условимся о следующих обозначениях. Пусть рассматривается некоторое (скалярное или векторное) поле a = a ( x , t ) . Тогда примем следующие обозначения (аргументы опущены): a = a ₀ + a ' + a "+ ..., где a ₀ — равновесное состояние поля, a ' — его возмущение первого порядка малости, a '' — возмущение второго порядка малости и т. д. Тогда справедливо следующее равенство для линейной акустики [2, с. 351]

Р' = (lp^ P = c2P, (7а) др

s где c =

I дp I                                      _

— скорость звука в среде, а ин-

N(др)s декс s означает взятие производной при постоянной энтропии (что и означает адиабатичность процесса). Отсюда получается простая связь возмущения плотности в зависимости от возмущения давления

P=^

c

Что касается той части возмущения давления, которая обусловлена изменчивостью температуры, то наиболее часто для ее получения при соблюдении некоторых ограничений пользуются системой уравнений Буссинеска [2, § 56].

Уравнения, описывающие свободную тепловую конвекцию, называются системой уравнений Буссинеска. При выводе этой системы уравнений принимается предположение о несжимаемости жидкости. Это означает, что изменением плотности под влиянием изменения давления можно пренебречь [2, с. 306]. Напротив, изменением плотности вследствие изменения температуры пренебречь нельзя. Возмущение температуры в жидкости приводит в общем случае (исключения см. в [2, § 3]) к появлению в жидкости внутренних течений, стремящихся перемешать жидкость так, чтобы в ней установилась постоянная температура. Такое, возникающее в поле тяжести движение, называют свободной конвекцией.

Возмущение плотности, обусловленное возмущением температуры, определяется из выражения [2, с. 306]

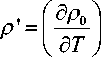
T ' = - P o в т '.

Здесь в =

1 (др I р (д Т J

— температурный коэффици- ент расширения жидкости.

В давлении p = p0 + p' величина невозмущенного давления p0 не остается постоянной, а меняется с высотой столба жидкости по гидростатическому закону p 0 = Po gY • x + const = - Po gz + const,       (9)

где x = ( x , y , z ) — координата точки среды, z отсчитывается вертикально вверх;     g = у g ;

Y = ( 0,0, -1) = — — единичный вектор, совпадаю-g щий по направлению с вектором ускорения силы тяжести.

С учетом сделанных предположений о несжимаемости жидкости и учете силы тяжести уравнение движения несжимаемой вязкой жидкости (1а) запишется в виде dv

P — + (v - V) v =

Idt ’

-V p + nA v + p g ,

или так [2, с. 307]

d v / x       V p    „

— + (v - V) v = —— + vAv + g,

η где v = — — кинематическая вязкость. После подстановки в последнее выражение значений p = P0 + P' и P = P0 + P', закона изменения гидростатического давления p0 (9) и значения из (8) для ρ ' окончательно получается уравнение движения для системы уравнений Буссинеска [2, с. 307]

— + (v-V) v =--Vp'+ vAv - вт'gY .     (10)

d t                P o

Знак минус перед последним членом справа имеет ясное физическое толкование: при T ' >  0, т. е. когда элементарный объем нагрет выше равновесной температуры T ₀ , выталкивающая архимедова сила действует в противоположном вектору g направлении, т. е. в положительном направлении оси Oz , направленной вверх.

Уравнение теплопереноса (энергии) (3а) для несжимаемой жидкости также упрощается, т. к. диссипативным членом D в случае свободной конвекции можно пренебречь по сравнению с остальными членами.³⁾ Кроме того, коэффицент теплопроводности κ при сделанных допущениях о малости величин T ' можно считать постоянным. Окончательно уравнение теплопереноса для свободной конвекции записывается в виде [2, с. 307]

дТ’

— + v -V T' = x A T ',            (11)

о t где x = К — коэффициент температуропро-ρ0cp водности жидкости.

Уравнения (10) и (11) вместе с уравнением неразрывности (6а)

div v = 0

представляют собой полную систему уравнений Буссинеска, описывающих свободную конвекцию [2, с. 307].

Замечание 1. При выводе системы уравнений Буссинеска (10), (11) и (6а) принималось допущение о несжимаемости жидкости. Условия допустимости такого приближения хорошо известны: в случае, когда скорость жидкости много меньше скорости звука в ней |v| □ c (малость числа Маха M ) [2, с. 41] и вариации температуры достаточно малы относительно ее равновесного значения T' □ Т0 [2, с. 277], жидкость можно считать несжимаемой. Для существенно нестационарных течений в [2, с. 41–42] приводится еще одно дополнительное условие приближения о несжимаемости жидкости: пусть τ и l — величины порядка промежутков времени и расстояний, на которых скорость жидкости испытывает заметное изменение (при периодическом процессе за τ принимается период), тогда необходимо выполне-l ние условия т >> — . c

Замечание 2. Основным допущением при выводе системы (10), (11), (6а) является предположение о том, что [13, с. 11] рассматривается в некотором смысле «слабая» конвекция : вызванные неоднородностью температуры отклонения плотности от среднего значения предполагаются настолько малыми, что ими можно пренебречь во всех уравнениях, кроме уравнения движения (выражение (10)), где это отклонение учитывается лишь в члене с подъемной силой. Однако сравнение результатов решения уравнений конвекции (10), (11), (6а) с обширным экспериментальным материалом с определенностью свидетельствует о том, что эти уравнения достаточно хорошо отражают все важные особенности тепловой конвекции в лабораторных масштабах.

ОБ ИСТОЧНИКЕ ТЕПЛОВОГО ИЗЛУЧЕНИЯ

Источник теплового излучения можно ввести, добавив некоторую функцию f (x, t) справа в уравнение теплопереноса (11) следующим образом [14, с. 26], [16, c. 32]:

— + v -V T' = x A T '+ f ( x , t ) .      (12)

_z , F (x , t )          , _x

Здесь f ( x , t ) = ——-, a F ( x , t ) ρ ₀ c_p

—

плотность

(удельная мощность) тепловых источников, равная количеству поглощаемого или выделяемого тепла в единице объема за единицу времени; [ F ( x , t )] = = ДжлГЧ'^-1; x = ( x , y , z ) — текущие координаты рассматриваемого объема.

РЕЗУЛЬТИРУЮЩИЕ УРАВНЕНИЯ

В заключение можно записать результирующие выражения для акустического и конвекционного случаев.

Для конвекционного случая это будет откорректированная с учетом стороннего источника тепла в уравнении теплопереноса (12) система уравнений Буссинеска с добавлением связи между возмущением плотности и температуры (8):

— + (v -V) v = —— Vp'+ vAv - вТ' gY, 5t

ST'                          .,.

— + v -V T ' = x A T ' + f ( x , t ) ,

div v = 0,

P' = p0 I T' = -peT'. (5 T J p0

Что касается акустического случая, то здесь можно пользоваться линейным волновым уравнением, например, для избыточного давления p ' (см., например, [2, § 64]) и связью (7а) между избыточным давлением и избыточной плотностью ρ ':

1 5 ² p' c² 5 t²

5 ² p' 5 ² p' 5 ² p' 5 x ² 5 y ² 5 z²

p ' = fl p ¹ P' = c ² P '^.

15 p ) s

+ ^ ( x , У , z , t ) ,

В (14) в волновом уравнении справа стоит стандартная акустическая функция источника.

СЛУЧАЙ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ (ОТСУТСТВИЕ КОНВЕКЦИИ)

Если в системе уравнений Буссинеска в уравнении теплопереноса (11) отсутствует конвективный член v -V T ', то уравнение (11) переходит в уравнение теплопроводности

ST'

"УТ = X ^A T ', 5 1

где нет других искомых полей и поэтому перестает быть связанным, т. е. может решаться автономно от других уравнений системы Буссинеска.

При осутствии конвективного члена глубина прогревания очень мала. В [15, с. 60] рассматривается модельный пример, в котором ставится краевая задача, когда к уравнению (11) добавляется краевое условие: на границе z = 0 полупространства z >  0 поддерживается переменная температура

— i ^ t

T ₀ e

T ( x , y , z = 0, t ) = T ₀ e^-'^mt ,         T ₀ = const.    (16)

Решение (13), (14) ищется в виде плоской волны

T ( x , У , z , t ) =

= T o exp [ i ( i ^ x ^{z -} m t ) ] = T o ^ex P ( ^- ^ x ^z ) ^e - ^{, m t} .    (17)

Подстановка (17) в (15) дает ξ_χ

. Величина

5x = 1 / ^x называется глубиной прогревания (на этом расстоянии от границы z = 0 амплитуда колебаний тепловой волны падает в e раз). Глубины прогревания для воздуха и для воды равны соответственно [15, с. 61]

5 _Х ( воздуха ) = 0.24 / Jf ; 5 _x ( воды ) = 0.021/ Jf .

Здесь f = m / 2 п — частота колебаний. Например, для частоты 500 Гц в воздухе глубина прогревания δ_χ составляет около 1 см, а для воды — порядка 1 мм.

Таким образом, в отсутствие конвекции распространением тепла можно пренебречь.

ОЦЕНОЧНЫЕ ЗНАЧЕНИЯ СКОРОСТЕЙ ПОТОКОВ ПРИ СВОБОДНОЙ КОНВЕКЦИИ

В работе [16, т. 1, с. 30] приведены оценки абсолютных значений скоростей при свободной конвекции. При оценках пренебрегают силами вязкости и другими явлениями, обычно оказывающими меньшее влияние, чем сила выталкивания Архи- меда. Тогда порядок амплитуды скорости оцени-

вается согласно выражению |v| = O

к

^

Lg

р )

, где

L — высота выталкивания (характерный параметр процесса свободной конвекции). Из этой оценки следует, что скорости течений, вызванные выталкивающей силой, малы. Например, в обычном по-

ле тяготения при выталкивании на разность высот L = 0.5 м и относительной разности плотностей, равной 2 % (— = 0.02), а также, если все-таки

ρ

учесть вязкие силы, оценочная величина скорости в воздухе будет иметь порядок |v| □ 8 см/с.

При конвективном теплообмене для случая свободной конвекции, когда движение вызывается разностью плотностей из-за неравномерности поля температур, важную роль играет число Грасгофа (критерий подобия) Gr

L = 0.1 м, g ~ 9.8 м/с² получаем из (18) оценку параметра VGr ~ 930, что соответствует течениям с числом Рейнольдса Re ® 930 на высоте 0.1 м от источника теплового излучения. Из (18) видно, что с ростом высоты L от источника наблюдения число Рейнольдса растет с порядком Re □ O ( L ^3/2).

Рассмотрим далее пограничный тепловой слой человека [16, с. 45]. Воздух в слое движется вверх под действием рассеяния с поверхности тела тепловой энергии, которая выделяется в организме. Эта энергия уносится восходящими потоками воздуха, образующимися вокруг тела. Движущими

механизмами процесса являются перенос тепла

и одновременно перенос водяного пара, выделяющегося при потении. Для типичного случая, когда температура кожи равна 33 ºС, а температура окружающего воздуха равна 25 ºС, вклад пере-

Gr = gL- в Т '•

ν ²

Ар носа тепла в величину составляет всего около

0.03, т. е. 3 %. Повышение влажности воздуха, вызванное потением, дает примерно такой же допол-

Здесь β — температурный коэффициент объемного расширения жидкости (для идеальных газов в = ^ [17, с. 37]; воздух при атмосферном давлении и комнатной температуре с большой точностью является идеальным газом); ν — кинематическая вязкость. Число Грасгофа представляет собой отношение выталкивающей силы и (или) создаваемой ею скорости к соответствующим величинам, обусловленным вязкостью [16, т. 1, с. 30].

Параметр Gr в условиях свободной конвекции играет роль, аналогичную числу Рейнольдса Re при вынужденных течениях. Аналогично критическому числу Reкр , критическое число Грасгофа Grкр определяет переход от ламинарного режима течения к турбулентному в условиях свободной (естественной) конвекции. Таким образом, число Грасгофа Gr , как параметр интенсивности течений, вызванных выталкивающей силой, замещает число Рейнольдса, являющегося параметром вынужденных течений [16, т. 1, с. 30].

Ар нительный вклад в величину . Таким образом,

А р суммарная величина ^ρ ясь приведенной выше скорости конвекции на

составляет 0.06. Пользу-

оценкой, получаем для разности высот 0.5 м

При заданных

ниже параметрах свободной

конвекции

β

1 Ар — АТ

в

1 А р ρ T '

воздухе

имеем

(при замене

I в Т ' ~ - — А Т =

^{1    1} р А Т

(       ^

Iv = O JgL^:

к

р J

V 9.8 - 0.5 - 0.06 » 54 см/с.

Примерно такую же оценку скорости конвек-

тивного течения можно получить из следующих предположений. При внешней температуре воздуха 20 ºС выходящий из легких человека воздух имеет температуру также примерно 33 ºС. Температурный коэффициент объемного расширения воздуха при температуре 20 ºС равен 3.43 - 10 — ³ 1/К. Тогда согласно приближенному ра-

Ар венству   вАт ~— имеем приближенно

ρ

Ар ~ вАТ = 3.43 -10-3 -13 ~ 0.045, что близко ρ к предыдущей оценке, несколько ей уступая по

Ар величине .

1 ^А — _Т• ρ T '

Ар

ρ

):

ВЫВОДЫ

Ар

ρ

= 0.02, v = 1.51 - 10 ^{- 5}

м2/с при 20 ºС,

В работе рассмотрено влияние акустического поля и поля свободной конвекции, вызванное тепловым источником на показатель преломления

света в однородной сплошной среде. Приведены соответствующие выражения для обоих полей, позволяющие рассчитать возмущения плотности среды, а, следовательно, возмущение показателя преломления света, вызванное возмущением плотности. Приведены конкретные порядки величины скорости при свободной конвекции, относительные величины изменения плотности, а также выражение для числа Грасгофа как параметра интенсивности течений при свободной конвекции. Материалы работы могут быть использованы в научном приборостроении при рассмотрении взаимодействия оптико-акустических и оптикоконвективных процессов.