Взаимодействие вакансий и атомов, образующих в альфа-железе растворы замещения

Вакансии играют важную роль во многих кинетических процессах в сплавах. Доля не заполненных атомами узлов кристаллической решётки, n или концентрация вакансий V , зависит прежде N всего от энергии их образования е V, которая представляет повышение полной энергии (точнее, энтальпии) кристалла при появлении одной вакансии. В выражении для свободной энергии чистого металла с вакансиями возрастание энергии компенсируется ростом конфигурационной и колебательной энтропии [1, 2], так что для определённой ,                                                   Г е^)

(равновесной) концентрации порядка exp I--I

I kT J свободная энергия системы оказывается минимальной. Прекрасный обзор экспериментальных данных о величинах е V и методиках измерения приведён в [2].

В бинарных сплавах замещения, которые являются предметом рассмотрения в данной работе, вакансии, совершая случайные перескоки по решётке, могут оказаться вблизи атома растворённого элемента. Для некоторых элементов между их атомами и вакансиями возникает притяжение, а фактически захват, который как бы выводит такие вакансии из группы равновесных. Тем самым возрастает общее количество вакансий. Будем считать, что энергии образования вакансии вблизи и вдали от примесного атома X равны е V0 и еVX соответственно. Тогда величина еЬ =е V 0 -е VX                               (1)

представляет энергию связи вакансии и растворённого атома. Обычно принимают, что е V 0 совпадает с энергией образования вакансии в основе сплава, в данном случае в а -железе [2].

Экспериментальные измерения еь обычно проводят, сравнивая равновесные концентрации вакансий в чистых металлах и сплавах на их основе. Погрешности таких измерений весьма значительны. Поэтому в настоящей работе было проведено первопринципное моделирование взаимодействия примесей замещения с вакансиями в а-железе, в основе которого лежат квантовомеханические методы расчёта энергии кристалла, содержащего дефекты, в рамках теории функционала электронной плотности.

Было изучено взаимодействие с вакансиями в а -железе атомов четырёх элементов: палладия, титана, ванадия и хрома. Расчёт электронной структуры проводился методом линейных присоединённых плоских волн (LAPW) с учётом обобщённого градиентного приближения (GGA) в программном пакете WIEN2k [3]. При моделировании были использованы следующие параметры: радиус muffin-tin сферы атомов железа R mt = 2,0 а.e.; параметр, контролирующий сходимость, R mt K max = 10; количество k -точек, характеризующее дискретную сетку, используемую для численного интегрирования по зоне Бриллюэна, n_k = 27. Был выбран параметр решётки a = 2,84 Å, являющийся равновесным для чистого ОЦК-железа [4]. В качестве модели была выбрана суперячейка, состоящая из 54 атомов. Для оценки энергии образования моновакансии в ОЦК-железе примерно в центре супер-ячейки был удалён один из атомов. Было определено значение энергии образования вакансии в чистом железе е V =2,15 эВ. Далее один из атомов Fe, находящийся в первом, втором либо третьем окружении относительно вакансии, поочерёдно замещался атомом примеси. Для получения более точного результата система, содержащая вакансию и примесь, была отрелаксирована.

Энергия образования точечного дефекта любого вида A определялась как разница между энергиями суперячейки, содержащей дефект, и супер-ячейки чистого железа:

s ( A ) = E ( A ) - E ref - E ( A ref ),                 (2)

где E ( A ) – энергия системы, содержащей дефект, E _ref – энергия чистого железа, а E ( A _ref) – энергия одиночного дефекта. В частности, при расчёте энергии образования вакансии в системе с примесью замещения X использовалась формула [5]:

^e VX = E Fe52- X -| E Fe53- X - E Fe54 | , ⁽³⁾

где E Fe52– X – энергия системы из 52 атомов Fe + вакансия + 1 атом X ; E Fe53– X – энергия системы из 53 атомов Fe + 1 атом X (без вакансии), а E Fe54 – энергия системы из 54 атомов чистого железа.

На рис. 1 представлена зависимость энергии образования вакансии в ОЦК-железе от положения атома палладия. Добавление примеси Pd к ОЦК-же-лезу снижает энергию образования вакансии; следовательно, образуется связанный комплекс V–Pd. Взаимодействие между вакансией и растворённым атомом наиболее сильно тогда, когда они расположены в ближайших соседних узлах решётки. Энергия связи в этом случае максимальна и равна 0,30 эВ. Если переместить атом палладия во вторую, третью и т. д. координационные сферы по отношению к вакансии, то энергия связи заметно уменьшается (см. таблицу и рис. 1).

Энергии связи с вакансиями в различных координационных сферах для атомов остальных трёх элементов (Ti, V, Cr) даны в таблице и на рис. 2. Отметим, что энергия связи и в этих случаях максимальна для позиций ближайших соседей. Удивительно, что во второй координационной сфере энергия связи V –Ti и V –V отрицательна, что отражает отталкивание, то есть перескок атомов в первую или третью сферу. У атома Cr энергия связи положительна и для второй сферы, но её значение мало. Полученные нами результаты согласуются с данными других расчётных работ [6, 7], а также

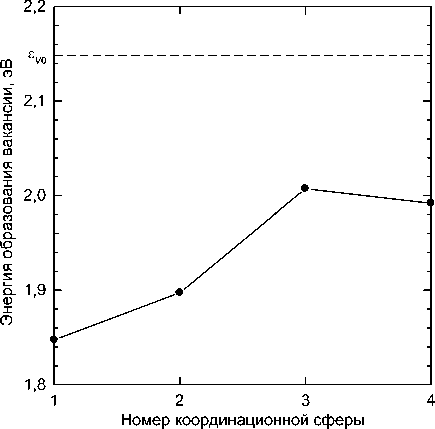
Рис. 1. Энергии образования вакансии при её расположении в различных координационных сферах относительно атома Pd в системе Fe 52 + вакансия + Pd (пунктирная линия соответствует энергии образования вакансии в чистом ОЦК-железе)

Энергии связи комплекса вакансия–атом замещения M

Атом замещения	Номер координационной сферы	Энергия связи, эВ
		Данная работа	[6]	[7]	Эксперимент [8]
Pd	1 2 3	0,30 0,25 0,14	–	0,36 0,26	0,21
Ti	1 2 3	0,28 –0,15 0,04	0,22	0,18 –0,11	0,16
V	1 2 3	0,08 –0,07 0,03	0,04	0,04 –0,06	<0,105
Cr	1 2 3	0,07 0,04 0,03	0,05	0,05 0,03	<0,105

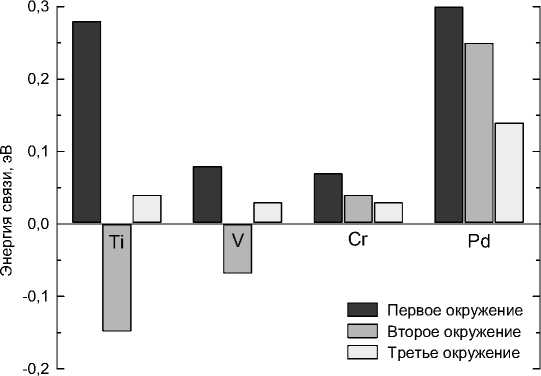
Рис. 2. Энергия связи вакансии и атома замещения, расположенного относительно неё в первой, второй и третьей координационной сфере

экспериментальными данными [1, 8]. Так, на основании данных об электросопротивлении сплавов Fe–Cr [1], энергия образования вакансии в железе увеличивается на 0,05 эВ на каждый атомный процент хрома; энергии связи примесей с вакансиями, найденные методом положительных мюонов [8], приведены в таблице.

Между вакансией и атомом замещения может возникать как упругое, обусловленное несоответствием размеров примеси и матричного атома, так и магнитное взаимодействие. Уменьшение энергии системы при добавлении к железу примесей, радиус которых превосходит радиус его атомов, связано с частичной компенсацией поля возмущений, создаваемого вакансией. Если бы взаимодействие между вакансией и атомом замещения было чисто упругим, то энергии связи вакансии с Ti и V имели бы бóльшие значения, чем с Pd, так как радиус Ti (1,47 Å) превосходит радиус Pd (1,37 Å), а радиус V сопоставим с ним (1,35 Å); напомним, что радиус железа составляет 1,24 Å. При этом Ti и V проявляют в такой системе антиферромагнитные свойства, тогда как атом Cr практически не взаимодействует с вакансией ввиду его близости к атомам Fe как по размеру, так и по свойствам. Таким образом, сложный характер взаимодействия примесей с вакансией вызван суперпозицией двух сопоставимых вкладов: упругого и химического.

Полученные данные об энергиях взаимодействия примесных атомов с вакансиями позволяют рассчитать эффект изменения равновесной концентрации вакансий при легировании железа исследованными элементами.

Предположим, что в твёрдом растворе замещения железа и элемента X , содержащем N _Fe и N_X атомов этих элементов, возникает n_V вакансий. Их NN атомные доли тогда равны x _Fe = —^-; x_X = —X и

взаимодействием ближайших соседей и введём вероятности событий, что данный ближайший узел решётки, соседствующий с вакансией, занят атомом железа:

P V - Fe =

AT         AT

V - Fe _ VF - Fe

znV

zNxV

или атомом элемента X :

p _ NV - X

P V - X = zn_V

N V - X

zNxV

,

(4 а )

(4 б )

где N V _{- Fe} и N V - _X представляют числа соответст-

вующих атомных пар, а z – координационное число решётки. Поскольку концентрация вакансий мала, то соседством вакансия–вакансия можно пренебрегать, и тогда N_{V - Fe} + N V - _X = zNx_V , а

P V - Fe ^{+ p}v - x = ¹.

В таком случае изменение энергии кристалла при образовании вакансии должно отражать лишь эффекты её взаимодействия с атомами Fe и X . Обозначим через e b энергию связи вакансии и растворённого атома X (положительную при притяжении и отрицательную при отталкивании). Тогда изменение энергии кристалла при образовании n_V вакансий

A E = n_V e _V - zn_VP_V - _X e b ,                   (5)

где e V - энергия образования вакансии в чистом

железе.

Происходящее при этом изменение свободной энергии твёрдого раствора, как обычно, равно

A G = A E - kT In W , (6) где W – термодинамическая вероятность рассматриваемой атомной конфигурации. Основываясь на статистически-термодинамическом подходе [9, 10], запишем W в следующем виде:

W 1 ■ W 2

W =------:--

( N - n_v )! n_v ! ^^неуМг^неуп

.

n xV = —, где N = NFe + NX + nV . Ограничимся

Здесь через W ₁ обозначено число способов размещения N_{V - Fe} пар V -Fe по zN _Fe парам, которые

атомы железа образуют с соседними узлами решётки, а через W 2 – число способов размещения N V - X пар V - X по zN X таким же парам, образуемым атомами X :

W 1 =

( zN Fe )!

^{( zN} Fe ^{- N} Fe - V )! N Fe - V !

W 2 =

( zN X )!

( ^zNx ^{- N}X - V ^{)! N}X - V

(8 а )

(8 б )

При этом N_{V - Fe} и N_V - X определяются соотношениями (4), в которых значения вероятностей P_{V - Fe} и P_{V - X} отражают существующий в растворе ближний порядок в расположении атомов замещения и вакансий. В условиях же полностью неупорядоченного размещения вакансий и атомов X по решётке ( W ₁^неуп и W ₂^неуп ) вероятности равны атомным долям: P_{V - Fe} = x _Fe; P_V - X = x_X .

Подставив эти значения в (8), (7) и далее в (6), получим с учётом формулы Стирлинга ln n ! ® n ln n - n общее выражение для изменения свободной энергии раствора при образовании n V вакансий:

A G = n_V s _V - zn V P V - X s b - kT [ N ln N - ( N - n V ) x x ln( N - n_V ) - n_V ln n_V - ( zN _Fe - zn_V + zn V P V _ X ) x x ln( zN _Fe - zn_V + zn V P V - X ) - ( zn_V - zn V P V - X ) x x ln ( zn_V - zn V P V - X ) - ( zN X - zn V P V - X ) x x ln( zN X - zn V P V - X ) - zn V P V - X ln( zn V P V - X ) + ^{+ ( zN} Fe ^{- zn}V^x Fe ^{)ln( zN} Fe ^{- zn}V^x Fe ) ^{+ zn}V^x Fe ^x ln( zn_Vx _Fe) + ( zN X - zn_Vx_X ) ln( zN X - zn_Vx_X ) + + zn_V x_X ln( zn_V x_X ) ] .                          (9)

Равновесное значение PV-X тогда можно най ти из соотношения ^^ = 0 . После дифферен-аPV - x цирования это соотношение приводит к квадратному уравнению относительно PV-X, положитель- ный корень которого равен

P V - X =

x _Fe h - x_V ( h + 1) + 1

2 x_V h

r x -1 +

k

4 x_X x_V h

^{1 +}-- 2

\    ( ^x Fe h ^{- x}V ⁽ h ⁺ 1) ⁺ 1 ) ,

где обозначено h = exp I —— I -1. Поскольку k kT J xV ^ 1, можно использовать разложение V1 + x ®

® 1 + x/2, и тогда выражение (10) приводится к виду

P V - X ”

x X    .

1 + x _Fe h

Это означает, что равновесные вероятности PV-X и PV-Fe практически не зависят от концентрации вакансий, что значительно облегчает дальнейшее рассмотрение.

Теперь найдём равновесное значение концентрации самих вакансий, которое определяется также из условия минимума свободной энергии dA G п                                  -

----= 0. После дифференцирования с учётом dnV соотношения (11) и малости xV получим выражение

Г s„ )Г.               Г Sk ))z xv = exP I- TV; II1 - xx + xx exP I     Il , (12)

k kT Jk              k kT J J в котором сомножитель xV = exp Г-^к I                        (13)

k kT J представляет долю вакансий в чистом железе.

Результаты нашего первопринципного моделирования дали для энергии образования вакансии значение s V =2,15 эВ. Авторами [6] и [11] было получено значение 2,17 эВ. Следует отметить, что эти величины находятся на верхнем пределе диапазона значений, наблюдавшихся экспериментально (от 1,4 ± 0,1 до 2,0 ± 0,2 эВ [12, 13]). А. Зеегер в обзоре [14] на основании литературных данных и собственных экспериментов пришёл к значениям s V = 1,61...1,75 эВ, а из результатов работы [15], где непосредственно измерялась концентрация вакансий после закалки от 1040 К, получил s V = 1,59 эВ. М.А. Штремель [2] считает наиболее надёжным значение s _V = 1,6 эВ. Авторы [12] показали, что повышение концентрации углерода в a -железе с 2^10 ^-5 до 1^10 ^-3 мас. % приводит к снижению наблюдаемой энергии образования вакансии с 1,79 ± 0,10 до 1,53 ^ 1,60 эВ; согласно первопринципным расчётам [6], энергия связи вакансии с атомом углерода составляет 0,60 эВ. Возможно, именно поэтому рассчитанное для чистого железа значение s V выше, чем в большинстве экспериментов, выполненных на железе технической чистоты. Кроме того, точное выражение для доли вакантных узлов имеет вид

о Га g I r As I  r sa xV = exP| -7^ l = exP| - V IexP| -X7 I, (14) k kT J k k J k kt J где AS - изменение энтропии колебательной подсистемы, обусловленное тем, что частота колебаний атомов вблизи вакансии (v‘) и вдали от неё (v) значительно различается; при использовании мо- v дели независимых колебаний атомов AS = zk ln — .

Следовательно, определяемая в эксперименте эффективная энергия образования вакансии, которая и входит в формулу (13), будет меньше истинной. Поэтому в дальнейших расчётах мы использовали экспериментальное значение s _V = 1,6 эВ.

Результаты расчётов температурной зависимости концентрации вакансий для двойных спла-

T , К

T , К

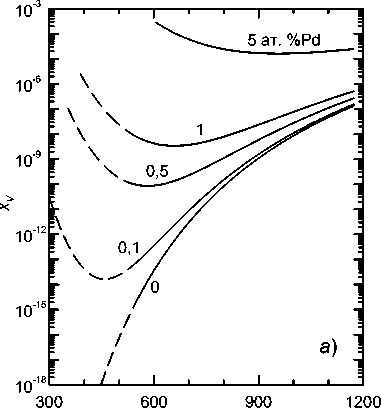
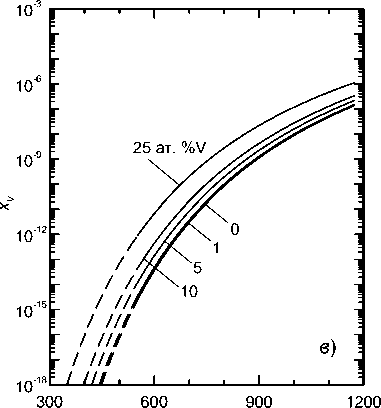
Рис. 3. Температурная зависимость доли вакантных узлов x _V , рассчитанная по формуле (12) при е V = 1,6 эВ и энергиях связи e b из таблицы для различных концентраций примесей Pd ( а ), Ti ( б ), V ( в ) и Cr ( г )

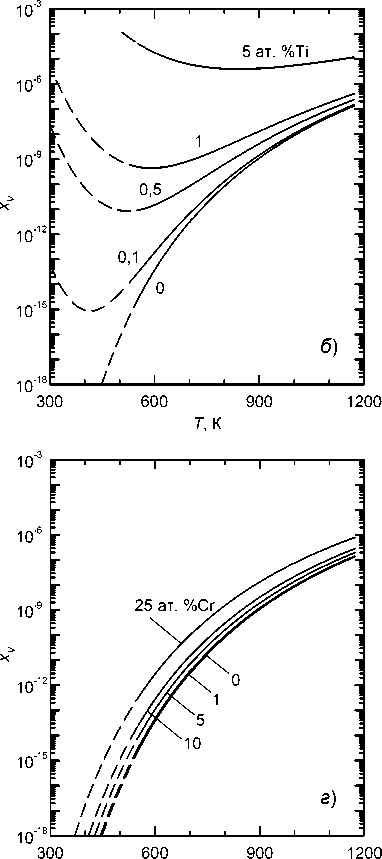
T , К

вов Fe с Pd, Ti, V и Cr разной концентрации приведены на рис. 3. Из него видно, что притяжение вакансий к примесным атомам приводит к тому, что в системах Fe–Pd и Fe–Ti, где энергия связи примеси с вакансией относительно велика (см. таблицу), заметно возрастает их равновесная концентрация; более того, при понижении температуры снижение концентрации вакансий может даже смениться ростом (рис. 3, а , б ).

В системах же Fe–V и Fe–Cr, где энергии связи примеси с вакансией в 3–4 раза меньше, даже значительно бóльшие концентрации примеси оказывают относительно небольшое воздействие на равновесную концентрацию вакансий: она возрастает примерно на порядок при концентрации xX = 0,25 (впрочем, не очевидно, что значения энергии связи εb из таблицы, рассчитанные для концентрации xX = 1/54 ≈ 0,019, сохранятся неиз- менными вплоть до таких высоких значений концентрации примеси).

Работа выполнена в рамках Государственного задания Министерства образования и науки РФ и частично поддержана грантом РФФИ 13-02-00048_а.