Взаимосвязь ключевой ставки Банка России и уровня инфляции в РФ

В данной работе проводится исследование взаимосвязи ключевой ставки Банка России и уровня инфляции.

Процентная политика центрального банка является одним из важнейших рыночных инструментов проведения денежно-кредитной политики. Она выражается в установлении и периодическом пересмотре официальных базовых ставок центрального банка, а также ставок по его основным операциям. Руководство Банка России использует ключевую процентную ставку для регулирования уровня инфляции в стране и заявляет об эффективности использования этого инструмента в борьбе с инфляцией. Целью работы является проверить существование связи между ключевой ставкой Банка России и уровнем инфляции в РФ.

В работе проводятся тест на причинность по Грейнджеру и тест на наличие коинтеграции, строятся модели ARIMA, коинтеграции и VAR. Предполагается, что ряды ключевой ставки и инфляции могут быть коинтегрированы, а если это не так, то интересно посмотреть, какие модели лучше описывают их поведение, отражают взаимосвязь и годятся для прогнозирования.

Данные по ключевой ставке для анализа были взяты с сайта Банка России [1]. Она измеряется в процентах годовых, были использованы её значения в последний день месяца. В работе используются ежемесячные данные в период с 01.2014 по 12.2021 (всего 96 наблюдений). Уровень инфляции по месяцам в годовом исчислении взят с сайта уровень-инфляции.рф [2]. Коэффициент инфляции используется в годовом исчислении, рассчитывается как сумма коэффициентов инфляции за 12 месяцев, включая выбранный. Такой способ позволяет оценить динамику изменения уровня инфляции в целом, сглаживая сезонные отклонения. Все вычисления по моделям проводились с помощью ППП GRETL (ряд ключевой ставки обозначен st, а уровня инфляции inf).

Определение порядков интегрируемости рядов

Первым шагом в анализе временных рядов является определение их порядков интегрируемости [3]. Для этого используется ADF тест Дики-Фуллера. В нем оценивается уравнение:

k

А У, = { ^ + ^0t } + P y_t - i + £ «Дy t — i + S i , i = 1

где взятые в фигурные скобки слагаемые могут отсутствовать, и тестируется гипотеза о разностно-стационарном ряде H : p = 0 ( y_t □ DS ) против альтернативы о тренд-стационарном ряде H 1 : p <  0( V . TS ).

Для проверки нулевой гипотезы используют обыкновенную t -статистику и сравнивают её с критическими значениями, которые зависят от наличия в уравнении константы и/или тренда и количества наблюдений.

Для первой разности ряда st нулевая гипотеза не отвергается. В модели со второй разностью в качестве зависимой переменной тестовая статистика -7,61, что меньше критического значения -1,95, нулевая гипотеза отвергается в пользу альтернативы о стационарности первой разности. Соответственно, исходный ряд st имеет первый порядок интегрируемости I(1).

и проверяют гипотезу

H ₀: 0 1 = 0 2 = ... = в _к = 0 с помощью F-теста. Если p-значение для коэффициентов перед лагами Х большие, то нулевая гипотеза не отвергается, и это значит, что ряд не является причиной по Грейнджеру для зависимого.

Была построена модель и получен вывод о том, что первая разность инфляции (d_inf) не является причиной по Грейнджеру для ряда первой разности ключевой ставки (d_st), а первая разность ключевой ставки является причиной по Грейнджеру для первой разности инфляции.

Для первой разности ряда inf нулевая гипотеза не отвергается и исходный ряд не стационарный. Во вновь оцененной модели со второй разностью в качестве зависимой переменной автокорреляции нет, тестовая статистика -5,05, что меньше критического значения -3,45, нулевая гипотеза отвергается в пользу альтернативы о стационарности первой разности. Соответственно, исходный ряд inf также является рядом первого порядка интегрируемости I(1).

Тест на причинность по Грейнджеру для рядов, приведенных к стационарному виду

Необходимо использовать стационарные первые разности рядов. Тест на причинность по Грейнджеру проверяет нулевую гипотезу об отсутствии влияния одного ряда на другой. Для этого строят модель:

kk

Z = AD + У aZ i +У 0Xt . +st 0 t                I    t—I                I     t—I       t i=1                  i=1

Из построенных моделей следует вывод, что ряд d_inf является зависимым, а ряд d_st влияющим.

Модель ARIMA для ряда ключевой ставки. Прогноз и доверительный интервал для прогноза на 1 шаг вперед

Т.к. первая разность инфляции не является причиной по Грейнджеру для ряда первой разности ключевой ставки, было решено построить модель ARIMA для ряда st. Наилучшая модель по информационным критериям получилась ARIMA (0,1,1). В пакете GRETL было получено уравнение:

A st = 0,0335465 + 0,319544 A st_M

Модель стационарна и обратима. Автокорреляция в модели отсутствует, нормальность, к сожалению, тоже. Коэффици- ент в модели получился значимым, константа нет. По коррелограмме остатки являются стационарными.

По графику (Рис.1.) видно, что прогнозные значения близки к истинным, оценённая модель хорошо отражает изменение ключевой ставки. Прогнозное значение на 1 шаг вперед 8,87, а доверительный интервал (7,17; 10,56), но стоит отметить, что при отсутствии нормальности остатков, доверительные интервалы не имеют информационной ценности. Реальное значение ключевой ставки в январе 2022 года было равно 8,5, т.е. в доверительный интервал всё же попадает.

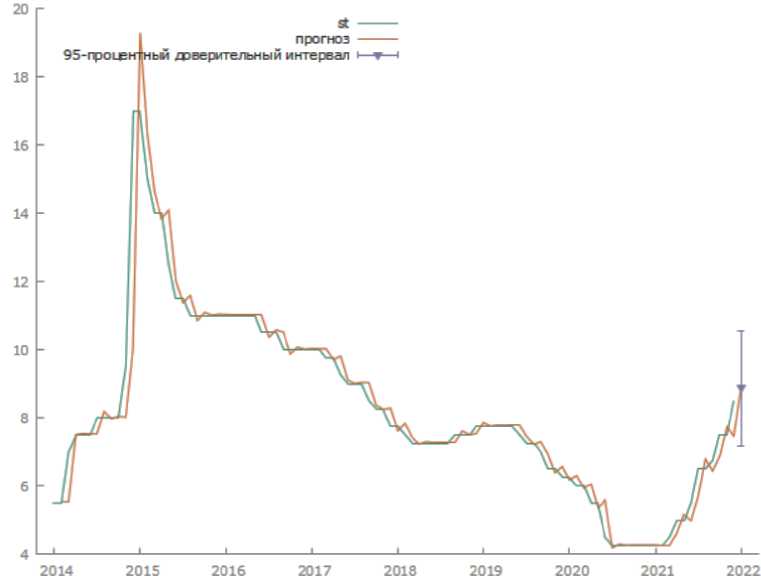
Рис. 1. Реальные и прогнозные значения ключевой ставки

Тест Ингла-Грейнджера на коинте-грациюрядов

Так как оба ряда st и inf являются I(1), то коинтеграция не исключена. Необходимо получить коинтегрирующий вектор.

Для этого по методу наименьших квадратов оценивается регрессия y_t = а + Px_t + ^ и вычисляются остатки e_t = y_t — а - Дх .

Затем оценивается уравнение вида:

k

а в, = рв,, + У а ав,;+v

t             t—1                 i      t—i         t i=1

и тестируется гипотеза Ho: p = 0 (ряд e принадлежит к классу DS, и коинтегра- ции    нет)    против    альтернативы

H : р <  0 (ряд в _t стационарен и коинтеграция есть).

Критические значения для этого теста лежат левее критических значений для теста Дикки-Фуллера. t-статистику сравни- вают со значениями специальных таблиц и, если tp < tKр, то нулевая гипотеза отвергается.

Ранее с помощью теста на причинность по Грейнджеру было определено, что ряд инфляции является зависимым, а ряд ключевой ставки влияющим. По МНК модель имеет вид:

inf = —2,103+1,036st.

( — 2,216)     (9,466)

Коэффициенты в модели значимы на 5% уровне, явных признаков ложной регрессии нет. В модели присутствует автокорреляция, это не очень хорошо, но важнее сохранить и проверить остатки на стационарность. В модели с остатками в качестве зависимой переменной тестовая статистика -2,218, критическое значение для нашей выборки на 5% -3,37, нулевая гипотеза не отвергается и ряд остатков мо- дели принадлежит к классу DS, коинте-грации нет.

VAR для рядов, приведенных к стационарному виду

Поскольку оба ряда I(1), модель VAR необходимо строить для их первых разностей. С помощью информационных критериев и тестов порядка лага было выявлено, что целесообразно строить модель 2 порядка:

Уравнение 1: d st

	коэффициент	ст. ошибка	t-статистика	р-значение
const	0,0143033	0,0903042	0,1584	0,8745
d st 1	0,229976	0,110077	2,089	0,0396   ••
d st 2	-0,265313	0,121913	-2,176	0,0322   **
d inf 1	0,244571	0,230903	1,059	0,2924
d_inf_2	-0,142387	0,198277	-0,7181	0,4746
Уравнение 2:	d_inf
	коэффициент	ст. ошибка	t-статистика	p-значение
const	-0,00274068	0,0406298	-0,06745	0,9464
d st 1	0,239243	0,0495258	4,831	5,71e-06   •••
d st 2	-0,111744	0,0548511	-2,037	0,0446     *•
d inf 1	0,982989	0,103888	9,462	4,59e-015  •••
d_inf_2	-0,331432	0,0892089	-3,715	0,0004     *•*

Рис. 2. Модель VAR для первых разностей рядов ключевой ставки и уровня инфляции

Тест отношения правдоподобия отвергает нулевую гипотезу, значит, порядок лага выбран верно. Тест на наличие автокорреляции не отвергает нулевую гипотезу об отсутствии автокорреляции в модели. Тест на нормальность остатков отвергает нулевую гипотезу о нормальном распределении. Модель стационарна. Остатки из обоих уравнений являются белым шумом.

В первом уравнении значимыми на 5% уровне являются только лаги самой переменной d_st, и F-тест для нулевых ограничений также не отвергает нулевую гипотезу о равенстве коэффициентов перед лагами d_inf нулю, следовательно, ряд первых разностей инфляции не является причиной по Грейнджеру для ряда первых разностей ключевой ставки, что подтверждает ранее сделанные выводы. R-квадрат мал (0,1). По p-значению уравнение в целом значимо на 5% уровне. Можно сделать вывод, что первое уравнение системы не является информативным.

Во втором уравнении все коэффициенты, кроме константы, значимы на 5% уровне. F-тест для нулевых ограничений отвергает нулевую гипотезу о равенстве коэффициентов перед лагами обеих переменных нулю. Ряд первых разностей ключевой ставки является причиной по Грейнджеру для ряда первых разностей инфляции. R-квадрат довольно большой (0,73). Уравнение в целом значимо.

Проанализировав прогнозы для разложения дисперсий, было получено, что первая разность ключевой ставки зависит от своих шоков на 98,5% и на 1,5% от шоков первой разности инфляции. Первая разность инфляции зависит от своих шоков на 66,3% и на 33,7% от шоков первой разности ключевой ставки.

Прогноз для ряда d_inf строим по второму уравнению (рис. 3).

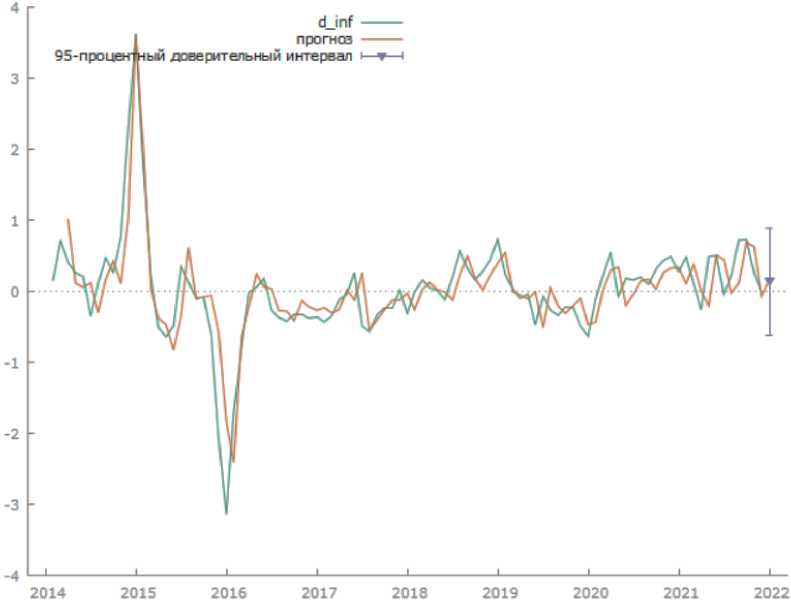
Рис. 3. Реальные и прогнозные значения первых разностей уровня инфляции

Прогнозные значения близки к реальным. Прогноз для первой разности инфляции на январь 2022 года составил 0,14, для исходного ряда это значит, что прогнозный уровень инфляции составит 8,53, реальное значение 8,74, что попадает в доверительный интервал.

Заключение

В работе было проведено исследование рядов ключевой ставки Банка России и уровня инфляции. Проверялась гипотеза о наличии коинтеграции в этих рядах, а также проводился анализ различных моделей с целью найти наиболее информативную для изучения взаимодействия данных показателей. В работе использовались ежемесячные данные в период с 01.2014 по 12.2021 (всего 96 наблюдений).

Было определено, что ряды являются первого порядка интегрируемости, что не исключало наличие коинтеграции. Тест на причинность по Грейнджеру показал, что ряд ключевой ставки оказывает влияние на ряд инфляции. Для ряда ключевой ставки была оценена модель ARIMA и построен прогноз на 1 шаг вперед. В результате те- ста Ингла-Грейнджера было выявлено, что коинтеграция в рядах всё-таки отсутствует. Также была построена модель VAR для рядов первых разностей, которая является наиболее информативной для анализа влияния ключевой ставки на уровень инфляции.

В ходе работы была отвергнута гипотеза о том, что ряды ключевой ставки и инфляции коинтегрированы. Для ряда ключевой ставки наиболее информативной оказалась модель ARIMA (0,1,1), а для ряда инфляции VAR (2) (2-е уравнение). Можно сказать, что приращение уровня инфляции зависит от двух собственных лагов и двух лагов приращения ключевой ставки.

Интересно отметить, что в большинстве статей, написанных на данную тематику, в качестве подтверждения своих экономических теорий авторы используют оценённую по МНК модель линейной зависимости (коинтеграции), что, как оказалось, не совсем корректно, т.к. в этой модели ложная регрессия.