Взаимосвязь температуры стеклования и параметров уравнения Вильямса - Ландела - Ферри

Автор: Сангадиев Сергей Шойжинимаевич, Сыдыков Булат Сергеевич, Сандитов Дамба Сангадиевич

Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu

Статья в выпуске: 3, 2014 года.

Бесплатный доступ

На основе релаксационной теории стеклования установлена определенная связь температуры стеклования с параметрами уравнения Вильямса - Ландела - Ферри для времени релаксации в области перехода жидкость - стекло.

Вязкость, релаксация, стеклование, скорость охлаждения

Короткий адрес: https://sciup.org/148182369

IDR: 148182369

Текст научной статьи Взаимосвязь температуры стеклования и параметров уравнения Вильямса - Ландела - Ферри

В физике аморфных органических полимеров [1], неорганических стекол [2], металлических аморфных сплавов (металлических стекол) [3] широкое распространение получило уравнение Вильямса – Ландела – Ферри (ВЛФ), успешно описывающее температурную зависимость времени релаксации τ(T) и вязкости η(T) в области стеклования [4]

ln a _T

C 1

T - T ^g

T - T + C ^g

где C 1 и С 2 – эмпирические параметры, T g – температура стеклования, a T – относительное время релаксации (относительная вязкость)

_ т ( T ) _ n ( T ) — — .

т ( ^T ₆ ) n ( ^T ₆ )

Это соотношение фактически эквивалентно известному уравнению Фогеля – Фульчера – Таммана (ФФТ) для вязкости [2, 4]

( B A n (T ) — n 0 exp I I.

V T T 0 /

Параметры уравнений ВЛФ и ФФТ связаны следующим образом [2] B = C 1 C 2 , T 0 = T g – C 2 .

Уравнение ВЛФ используется при прогнозировании механических и тепловых свойств аморфных полимеров и стекол [1, 5].

Задача работы – установить количественную связь постоянных уравнения ВЛФ с температурой стеклования аморфных веществ.

Теоретическая часть

Среди различных подходов к переходу аморфного вещества из жидкого в твердое стеклообразное состояние важное место занимают релаксационные теории [6-11], согласно которым в процессе стеклования важную роль играет соотношение между временем релаксации τ и скоростью охлаждения расплава q = dT/dt. Релаксационная теория Волькенштейна – Птицына [7] приводит к следующей связи между этими величинами:

( d т A

I I — v dT j t—Tg

Подстановка τ(T) из уравнения ВЛФ (1) в условие стеклования (2) позволяет получить взаимосвязь скорости охлаждения q и времени релаксации τ(Tg) = τg при температуре стеклования qτg = C,(3)

где величина C определяется отношением параметров уравнения ВЛФ

C = C2/C1 .(4)

Соотношение (3) было предложено ранее Бартеневым [6] из общих соображений. Чем больше q, тем меньше τ_g и, следовательно, тем выше T_g. Уравнение Бартенева (3) используется при установлении зависимости температуры стеклования от скорости охлаждения T g = T g (q) и в других случаях [5, 6, 11].

Авторы [7] ограничились простейшим случаем, когда в уравнении времени релаксации [12]

( и A т — т 0 exp I I (5)

V kT J энергия активации перехода молекулы из основного в возбужденное состояние U не зависит от температуры: U = const (τ0 – период колебания молекулы). Подстановка зависимости (5) в соотношение (2) при этих условиях приводит к результату [7]

( kT 2 А qT g = [_ U J. (6)

При данном подходе параметр уравнения Бартенева C приобретает следующий физический смысл:

C =[ U J T g . (7)

Сравнение с экспериментом. Обсуждение результатов

В табл. 1-4 приводятся значения параметра C, вычисленные по формуле (4) по данным об эмпирических постоянных уравнения ВЛФ C 1 и C 2 . Как видно, у аморфных веществ одного класса величина С является практически постоянной. У аморфных органических полимеров она равна С ≈ (1-2)K (табл. 1), а у силикатных стекол С ≈ (7-10)K (табл. 2). Металлические стекла по значениям С ≈ (2-4)K (табл. 3) занимают промежуточное положение между аморфными полимерами и силикатными стеклами [13]. Величина С ≈ 1.8K у стеклообразного селена (табл. 1), принадлежащего к классу неорганических стекол, совпадает с данными для органических линейных аморфных полимеров. Этот факт согласуется с представлением о том, что стеклообразный селен является линейным неорганическим полимером с цепочечной структурой –Se–Se–Se–. Калиевоборатные стекла, у которых С ≈ (3-4)K (табл. 4), можно рассматривать как неорганические полимеры с линейно-разветвленной структурой [2].

Таблица 1

Параметры уравнения ВЛФ и постоянные C, C* и С 0 для селена, аморфных полимеров и ряда органических стеклующихся жидкостей

№	Стекло	T g , K	C 1	C2, K	C, K^-1	C*∙10³	С 0	Литература
1	Поливинилацетат	305	36	47	1.3	4.3	0.85	[1]
2	Натуральный каучук	300	38	54	1.4	4.7	0.82	[1]
3	Метакрилат этиловый Трибутират целлюлозы в диметилфталате (мас. %)	335	40	65	1.6	4.9	0.81	[1]
4	21	188	48	43	0.9	4.8	0.77	[1]
5	43	193	54	39	0.7	3.7	0.80	[1]
6	Селен	303	32	58	1.8	6.0	0.81	[2]
7	Пропанол	98	41	25	0.6	6.2	0.74	[16]
8	Протиленгликоль	160	44	40	0.9	5.7	0.75	[16]
9	Глицерин	185	42	53	1.3	6.8	0.71	[16]

Известно, что подавляющее большинство стеклующихся жидкостей (расплавов неорганических стекол, аморфных органических полимеров, аморфных металлов) переходит в твердое стеклообразное состояние при достижении одной и той же «универсальной» вязкости: η(Tg) ≈ const ≈ 1012 Па∙с. Этому высокому значению «вязкости стеклования» соответствует время релаксации при температуре стеклования [2]

τ(T g ) ≈ τ g ≈ const ≈ 10² с.

Период колебания частицы около равновесного состояния составляет τ 0 ≈ const ≈ 10^-12 с.

Принимая во внимание эти значения τg и τ0 в уравнении времени релаксации (5), при T = Tg имеем [14, 15]

kT ( ¹²

----g- = - In I ' I » - In I ¹⁰-------- I » const » 0 .031 .

U | т J ( 10 ² c J

С учетом «универсального» равенства (8) параметр уравнения Бартенева (7) должен быть пропорционален температуре стеклования: С ~ T_g. Отсюда, согласно соотношению (4), следует ожидать линейной корреляции между отношением постоянных уравнения ВЛФ (C₂/C₁) и температурой стеклования T_g. В самом деле, зависимость C 2 /C 1 от T g у щелочносиликатных и ряда других стекол оказывается линейной (рис. 1-3)

C 2 ~ T (9)

_C ₁ g .

Поскольку C 1 ≈ const у стекол одного структурного типа (табл. 1-4), между C 2 и T g наблюдается линейная корреляция: C 2 ~ T g (рис. 4). В связи с этим уравнение ВЛФ (1) можно представить в виде

ln a _T

T - T

C g ,

¹ T - С 0 T g

где безразмерная величина C0

С 2

слабо зависит от природы стекол: C0 ≈ const (табл. 1–4). Можно разделить обе части соотношения (3) на температуру стеклования и ввести обозначение:

Таблица 2

Параметры уравнения ВЛФ и постоянные C, C* и С0 для щелочносиликатных и ряда многокомпонентных силикатных стекол R2O–SiO2 [17]

№	Содержание R₂O (мол. %) в стекле	T g , K	C 1	C 2 , K	C, K^-1	C*∙10³	C 0
1	Li 2 O 30.0	668	37	249	6.7	10.1	0.63
2	35.9	680	35	267	7.6	11.2	0.61
3	41.3	675	34	220	6.5	9.6	0.67
1	Na 2 O 19.6	744	34	337	9.9	13.3	0.55
2	30.1	713	35	238	6.8	9.5	0.67
3	32.9	704	36	275	7.6	10.9	0.61
4	36.2	694	34	246	7.2	10.4	0.65
1	K 2 O 16.7	766	33	356	10.8	14.1	0.54
2	21.4	745	34	356	10.5	14.1	0.52
3	26.9	733	36	392	10.9	14.9	0.47
4	31.2	720	35	350	10.0	13.9	0.51
1	БФ–12	759	34	196	5.8	7.6	0.74
2	БК–9	851	32	192	6.0	7.1	0.77
3	Листовое	807	36	305	8.5	10.5	0.62

Таблица 3

Параметры уравнения ВЛФ и постоянные С, C* и С0 для металлических стекол [18]

№	Металлические стекла	T g , K	C 1	C 2 , K	C, K^-1	С*∙10³	С 0
1	Ni 62.4 Nb 37.6	945	40	135	3.4	3.6	0.86
2	Ni 75 Si 8 B 17	782	38	112	2.9	3.8	0.86
3	Fe 91 B 9	600	53	87	1.6	2.7	0.86
4	Fe 89 B 11	640	37	125	3.4	5.3	0.80
5	Fe 83 B 17	760	38	122	3.2	4.2	0.84
6	Fe 41.5 Ni 41.5 B 17	720	38	119	3.1	4.3	0.83
7	Fe 79 Si 10 B 11	818	38	117	3.1	3.8	0.86
8	Fe 80 P 13 C 7	736	38	120	3.2	4.3	0.84
9	Pd 82 Si 18	657	37	100	2.7	4.1	0.85
10	Pd 77.5 Cu 6 Si 16.5	653	38	100	2.6	4.0	0.85
11	Pd 40 Ni 40 P 20	602	39	93	2.4	4.0	0.85
12	Pt 60 Ni 15 P 25	500	37	95	2.6	5.1	0.81
13	Co 75 Si 15 B 10	785	38	110	2.9	3.7	0.86

Таблица 4

Параметры уравнения ВЛФ и постоянные С, C* и С0 для калиевоборатных стекол K2O–B2O3 [17]

№	Содержание K₂O (мол. %) в стекле	T g , K	C 1	C 2 , K	C, K^-1	С*∙10³	С 0
1	0	578	30	121	4.0	7.0	0.79
2	1.1	582	30	98	3.3	5.6	0.83
3	2.1	586	30	89	3.0	5.1	0.85
4	3.9	597	31	100	3.2	5.4	0.83
5	8.5	623	33	117	3.5	5.7	0.81
6	11.6	647	34	131	3.9	6.0	0.80
7	23.5	712	36	140	3.9	5.5	0.80
8	31.5	710	38	153	4.0	5.7	0.78
9	34.4	701	38	142	3.7	5.3	0.80

с учетом которого уравнение (3) принимает вид

q тg = С V

В таком варианте обе части равенства являются безразмерными величинами и новая постоянная C* слабо зависит от природы стекол (табл. 1-4).

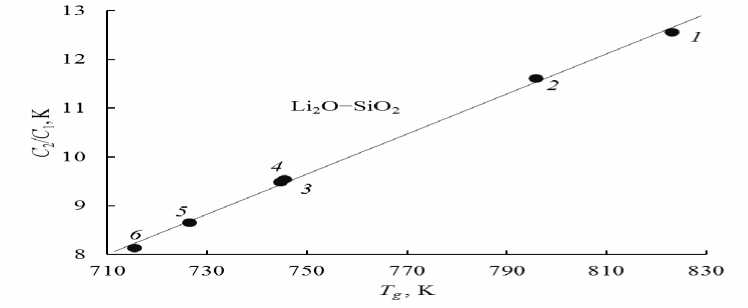
Рис. 1. Линейная корреляция между отношением параметров уравнения ВЛФ C₂/C₁ и температурой стеклования T_gдля литиевосиликатных стекол. Содержание Li₂O, мол. %: 1 – 10, 2 – 14 , 3 – 25, 4 – 25, 5 – 30, 6 – 33.3

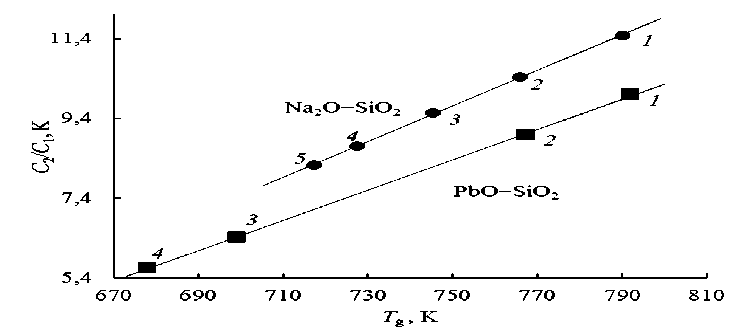
Рис. 2. Линейная корреляция между отношением параметров уравнения ВЛФ C₂/C₁ и температурой стеклования T_gдля натриевосиликатных и свинцовосиликатных стекол. Содержание Na₂O, мол. %: 1 – 15, 2 – 20 , 3 – 25, 4 - 30, 5 – 33 . Содержание PbO, мол. %: 1 – 24.6, 2 – 30, 3 – 45, 4 – 50

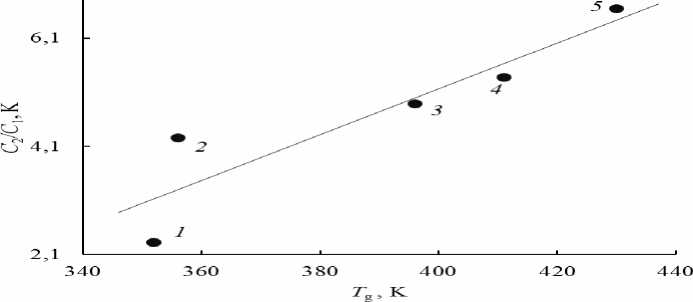
Рис. 3. Линейная корреляция между отношением параметров уравнения ВЛФ C₂/C₁ и температурой стеклования T_gдля халькогенидных стекол Ge-Se. Содержание Ge, мол. %: 1 – 7.4, 2 – 9.27 , 3 – 13.96, 4 – 15.85, 5 – 18.69

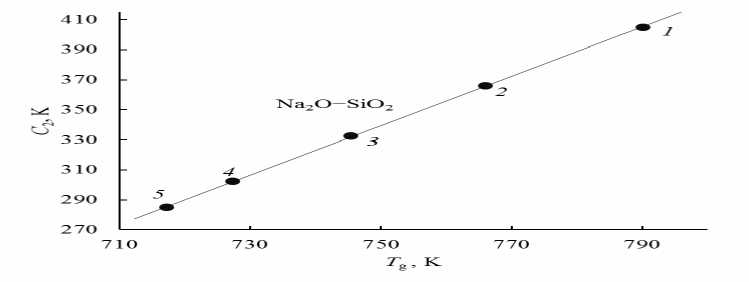
Рис. 4. Линейная корреляция между отношением параметров уравнения ВЛФ C₂ и температурой стеклования T_gдля натриевосиликатных стекол Na 2 O-SiO 2 . Содержание Na 2 O, мол. %: 1 – 15, 2 – 20 , 3 – 25, 4 – 30, 5 – 33

Заключение

Таким образом, между отношением параметров уравнения ВЛФ С2/C1 и температурой стеклования Tg у ряда стекол наблюдается линейная корреляция. Это позволяет записать уравнение ВЛФ в модифицированной форме, где фигурируют две безразмерные практически «универсальные» постоянные C1 и C0.

Список литературы Взаимосвязь температуры стеклования и параметров уравнения Вильямса - Ландела - Ферри

Ferry J.D. Viscoelastic Properties of Polymers. -NY: Wiley, 1961. -122 p.
Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. -Новосибирск: Наука, 1982. -269 с.
Сандитов Д.С., Сангадиев С.Ш., Сандитов Б.Д. Флуктуационный свободный объем металлических стекол//Физика и химия стекла. -2000. -Т. 26, № 1. -С. 84-90.
Williams M.L., Landel R.F., Ferry J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids1//J. Amer. Ghem. Soc. -1955. -V. 77, № 14. -P. 3701-3707.
Бартенев Г.М., Бартенева А.Г. Релаксационные свойства полимеров. -М.: Химия, 1992. -394 с.
Бартенев Г.М. О зависимости температуры стеклования силикатного стекла от скорости охлаждения//ДАН СССР. -1951. -Т. 76, № 2. -С. 227-230.
Волькенштейн М.В., Птицын О.Б. Релаксационная теория стеклования//ДАН СССР. -1955. -Т. 103, № 4. -С. 795798.
Narayanaswamy O.S. Model of structural relaxation in glass//J. Phys. Ghem. -1971. -V. 54, № 10. -P. 491-498.
Moynihan G.T., Easteal A.J., Wilder J., Ticker J. Dependence of the glass transition temperature on heating and cooling//J. Phys. Ghem. -1974. -V. 78, № 26. -P. 2673-2677.
Мазурин О.В. Стеклование. -Л.: Наука, 1986. -160 с.
Бартенев Г.М., Лукьянов И.А. Зависимость температуры стеклования аморфных веществ от скорости нагревания и связь температуры стеклования с энергией активации//Журн. физ. химии. -1955. -Т. 29, № 8. -С. 1486-1498.
Френкель Я.И. Кинетическая теория жидкостей. -М. -Л.: Наука, 1975. -424 с.
Сандитов Б.Д., Сангадиев С.Ш., Сандитов Д.С. Время релаксации и скорость охлаждения жидкости в области стеклования//Физ. и хим. стекла. -2007. -Т. 33, № 5. -С. 620-631.
Бартенев Г. М., Сандитов Д. С. Об энергии активации процесса стеклования кварцевого стекла и силикатных стекол//ДАН СССР. -1989. -Т. 304, № 6. -С. 1378-1384.
Сандитов Д.С., Бартенев Г.М. Энергия активации и температура стеклования//Высокомолек. соед. Б. -1989. -Т. 30, № 10. -С. 748-751.
Дуров В.А., Шахпаронов М.И. Теория коллективных реакций в жидкой фазе. VI. Уравнение Вильямса-Ландела-Ферри//Журн. физ. химии. -1979. -Т. 53, № 10. -С. 2456-2459.
SciGlass: Database and information system. Version 7.0. Premium edition ITG. Inc. -2008. -URL: www.sciglass.info.
Судзуки К., Фудзимори Х., Хасимото К. Аморфные металлы. -М.: Металлургия, 1987. -328 с.

Еще

Статья научная