Взаимосвязь задач поперечного изгиба и свободных колебаний треугольных пластинок
Автор: Коробко В.И., Бояркина О.В.
Рубрика: Теоретичские исследования
Статья в выпуске: 22 (94), 2007 года.
Бесплатный доступ
С помощью численного эксперимента исследуется функциональная i»T * связь между интегральными физическими характеристиками в задачах ,F ,:. поперечного изгиба и свободных колебаний упругих пластинок в виде £*» * равнобедренных треугольников с однородными и комбинированными * >! граничными условиям
Короткий адрес: https://sciup.org/147154171
IDR: 147154171 | УДК: 624.074.04
Текст научной статьи Взаимосвязь задач поперечного изгиба и свободных колебаний треугольных пластинок
Известно [1, 2], что интегральные физические характеристики пластинок (максимальный прогиб w0 и основная частота колебаний со) функционально связаны с площадью пластинки А, её цилиндрической жёсткостью D, видом нагрузки q(x.y) и массой единицы площади т;
<уЛ2 2 4 О
—, со = В —
° D mA2
где коэффициенты пропорциональности аир зависят от формы пластинки (Ф) и условий на границе (Г):
а=/Ф, Г), р = Ф(Ф, Г).
Если умножить левые и правые части выражения (1) друг на друга, то получится результат, не зависящий от площади пластинки и цилинд- рической жесткости (вида материала):
= (2)
т т где К = ар4.
Детальное изучение этого произведения, когда в задаче поперечного изгиба пластинок внешняя нагрузка является равномерно распределенной (_q(x,y) = q), проведено в работах [3, 4], где с помощью численного эксперимента показано, что для всего множества упругих изотропных пластинок с выпуклым контуром и произвольными граничными условиями произведение коэффициентов пропорциональности К = ар4, представленное в координатных осях К - Kf (где Kf - коэффициент формы пластинки [5]), с погрешностью, не превышающей (5...6)%, вырождается в одну плавную и монотонную кривую. Это свидетельствует о том, что интегральные физические параметры пластинок w0 и со функционально связаны между собой, а произведение К = ар4 не зависит от граничных условий, а зависит только от коэффициента формы пластинок Kf.
Коэффициент формы пластинки Kf численно характеризует её «правильность» (симметричность) и определяется контурным интегралом
С помощью численного эксперимента исследуется функциональная связь между интегральными физическими характеристиками в задачах поперечного изгиба и свободных колебаний упругих пластинок в виде равнобедренных треугольников с однородными и комбинированными граничными условиями.
= min$™, где ds - длина элементарного участка на границе контура пластинки; h ~ длина перпендикуляра, опущенного из полюса, взятого внутри области, на касательную к переменной точке контура. Подробные исследования этой геометрической характеристики проведены в статье [5].
Проведем исследование взаимосвязи интегральных физических параметров w0 и со для пластинок в виде равнобедренного треугольника. За основу возьмем решения, полученные в работе [6] с помощью МКЭ и с использованием программного комплекса «Лира» (см. таблицу, колонки 3 и 4).
Анализ этих решений показал, что для пластинок в
виде равностороннего треугольника полученные результаты незначительно (в пределах одного процента) отличаются от известных точных и приближенных решений, найденных с высокой точностью, которые приводятся в известной справочной и научной литературе [1, 2].
Для исправления этой систематической по- грешности при решении рассматриваемой задачи с помощью программного комплекса «Лира» были введены поправочные коэффициенты К, и Кщ, которые позволили с высокой точностью удовлетворить известным решениям.
Исправленные таким образом результаты и представлены в таблице в колонках 3 и 4. По этим данным построены аппроксимирующие функции 1/ш2 - w0 и w0 - 1/ю2, графики которых изображены на рисунке. Оказалось, что эти функции хорошо описываются линейными зависимостями:
1/ш2 =(а; +ЬА -а)- А2 -m/D, (3)
где at = 1,993 7-Ю”6, 6t = 0,6226;
w0=10”3(S2+62/^4)-^2/Z), (4)
где а2= -0,010267, Ы = 1608,599. Очевидно, приведенные зависимости будут справедливы и для пластинок в виде равнобедренного треугольника с произвольным законом изменения граничных условий (любая комбинация жёсткого защемления и шарнирного опирания вдоль их сто-рон)Расчеты, проведенные по формулам (3) и (4) представлены в таблице в колонках 6 и 8. Анализ этих результатов показывает:
Коробко В.И., Бояркина О.В.
Взаимосвязь задач поперечного изгиба и свободных колебаний треугольных пластинок
Значения максимального прогиба и основной частоты колебаний пластинок в виде равнобедренного треугольника и взаимосвязь этих параметров
|
Вид опирания |
Угол при вершине основании |
Решения по МКЭ |
Решения по (1) |
Решения по (2) |
|||
|
а-103 |
Р2 |
Р2 |
Д, % |
аЮ3 |
Д,% |
||
|
1 |
2 |
3 |
4 |
6 |
7 |
8 |
9 |
|
1/ю2 = (1,9937 ■ 10 6 + 0,6226 ■ а)-1/-12 -тр; (1) w0 =10~Ч-- 0,010267+1608,599,^ (2) |
|||||||
|
Шарнирное опирание по всем сторонам пластинки |
20/80 |
1,625 |
31,31 |
31,40 |
+0,29 |
1,631 |
+0,37 |
|
30/75 |
2,335 |
26,17 |
26,21 |
+0,15 |
2,338 |
+0,13 |
|
|
40/70 |
2,741 |
24,22 |
24,19 |
-0,13 |
2,732 |
-0,33 |
|
|
50/65 |
3,013 |
23,05 |
23,08 |
+0,13 |
3,017 |
+0,13 |
|
|
60/60 |
3,086 |
22,79 |
22,80 |
+0,04 |
3,087 |
+0,03 |
|
|
70/55 |
3,035 3,026 |
23,05 23,06 |
23,08 23,03 |
+0,13 +0,13 |
3,017 3,015 |
-0,59 -0,36 |
|
|
80/50 |
2,837 2,845 |
23,70 23,74 |
23,78 23,75 |
+0,33 +0,04 |
2,853 2,844 |
+0,92 +0,04 |
|
|
90/45 |
2,630 |
24,75 |
24,70 |
+0,20 |
2,616 |
-0,53 |
|
|
100/40 |
2,313 |
26,31 |
26,33 |
+0,07 |
2,314 |
+0,04 |
|
|
110/35 |
1,990 1,982 |
28,47 28,43 |
28,39 28,44 |
-0,28 -0,04 |
1,974 1,980 |
-0,80 -0,10 |
|
|
Боковые стороны пластинки шарнирно оперты, а основание жестко защемлено |
20/80 |
1,315 1,321 |
34,68 34,79 |
34,91 34,83 |
+0,66 +0,11 |
1,327 1,318 |
+0,91 -0,23 |
|
30/75 |
1,754 |
30,17 |
30.23 |
+0,20 |
1,757 |
+0,17 |
|
|
40/70 |
1,960 |
28,54 |
28,60 |
+0,21 |
1,965 |
+0,25 |
|
|
50/65 |
2,019 |
28.21 |
28,18 |
-0,11 |
2,011 |
-0,40 |
|
|
60/60 |
1,967 |
28,54 |
28,55 |
+0,04 |
1,965 |
-0.10 |
|
|
70/55 |
1,843 |
29,55 |
29,50 |
-0,17 |
1,832 |
-0,60 |
|
|
80/50 |
1,667 |
31,02 |
31,01 |
-0,03 |
1,661 |
-0,36 |
|
|
90/45 |
1,456 |
33,07 |
33,18 |
+0,33 |
1,461 |
+0,34 |
|
|
100/40 |
1,247 1,241 |
35,93 35,88 |
35,84 35,93 |
-0,25 +0.13 |
1,236 1,239 |
-0,88 -0,16 |
|
|
110/35 |
0,992 1,007 |
39,48 39,83 |
40,17 39,87 |
+1,75 +0,10 |
1,022 1,004 |
+3,02 -0,30 |
|
|
Боковые стороны пластинки жестко защемлены, а основание шарнирно оперто |
20/80 |
0,513 0,515 |
55,14 55,46 |
55,78 55,67 |
+1,16 +0,41 |
0,519 0,513 |
+1,17 -0,39 |
|
30/75 |
0,819 0,820 |
43,93 44,06 |
44,20 44,17 |
+0,61 +0,25 |
0,823 0,818 |
+0,49 -0,24 |
|
|
40/70 |
1,058 |
38,92 |
38,90 |
-0,05 |
1,052 |
-0,57 |
|
|
50/65 |
1,213 |
36,34 |
36,34 |
0,00 |
1,208 |
-0,41 |
|
|
60/60 |
1,296 |
35,07 |
35,16 |
+0,27 |
1,298 |
+0,15 |
|
|
70/55 |
1,316 1,311 |
34,95 34,92 |
34,89 34,96 |
-0,17 -0,11 |
1,307 1,309 |
-0,68 -0,15 |
|
|
80/50 |
1.275 |
35,32 |
35,45 |
+0,37 |
1,279 |
+0,31 |
|
|
90/45 |
1,183 |
36,62 |
36,80 |
+0,49 |
1,189 |
+0,51 |
|
|
100/40 |
1,054 |
38,77 |
38,98 |
+0,53 |
1,060 |
+0,38 |
|
|
110/35 |
0,882 0,898 |
41,70 42,14 |
42,59 42,22 |
+2,13 +0,19 |
0,915 0,896 |
+3,74 -0,22 |
|
|
Жесткое защемление по всем сторонам пластинки |
20/80 30/75 |
0,430 0,430 0,643 |
60,14 60,52 49,56 |
60,89 60,61 49,85 |
+1,25 +0,15 +0,58 |
0,434 0,429 0,645 |
+0,93 -0,23 +0,31 |
|
40/70 |
0,785 0,787 |
44,83 44,95 |
45,08 45,08 |
+0,49 +0,29 |
0,790 0,786 |
+0,64 -0,13 |
|
|
50/65 |
0,856 |
43,07 |
43,23 |
+0.33 |
0,857 |
+0,12 0,00 |
|
|
60/60 |
0,880 |
42,51 |
42,64 |
+0,31 |
0,880 |
||
|
70/55 |
0,858 |
43.07 |
43,18 |
+0,25 |
0,857 |
-0,12 |
|
|
80/50 |
0,790 0,803 |
44,63 44,50 |
44,94 44,63 |
+0,69 +0,29 |
0,797 0,802 |
+0,89 -0,12 |
|
|
90/45 |
0,723 |
46.96 |
47,02 |
+0,13 |
0,719 |
-0,55 |
|
|
100/40 |
0,610 0,623 |
49,88 50,53 |
51,18 50,65 |
+0,60 +0,24 |
0,636 0,620 |
-4,26 -0,48 |
|
Серия «Строительство и архитектура», выпуск 5
Теоретические исследования
-
1. Для пластинок с углами при вершине у от ЗОо до 100о эти формулы дают результаты, отличные от найденных с помощью МКЭ, в пределах одного процента (см. колонки 7 и 9 в таблице).
-
2. Для пластинок с острыми углами при у < 20° и у > 100° эта погрешность возрастает, хотя и не превышает 4,5%. В приведенной таблице жирным шрифтом выделены результаты, которые дают погрешность, превышающую 0,50%.
-
3. Отмечается немонотонность решений, полученных с помощью МКЭ для пластинок с острыми углами. При некоторых значениях острых углов наблюдаются «всплески» (резкие отклонения решений, достигающие 4,5%), которые затем исчезают при незначительном изменении углов пластинки. Эти всплески объясняются неустойчивостью решений, получаемых с помощью МКЭ при наличии весьма острых углов в пластинках.
-
4. Указанные всплески наблюдаются и для максимального прогиба, и для основной частоты колебаний пластинок. Их нетрудно сгладить, если взять средние значения результатов, полученных с помощью МКЭ и с помощью функций (3) и (4). Такие сглаженные результаты приведены ниже соответствующих строк таблицы, выделенных жирным шрифтом. Эти новые результаты, очевидно, можно считать более точными, поскольку они не противоречат общей тенденции монотонного изменения интегральных физических характеристик треугольных пластинок при постепенном изменении угла при вершине треугольника, хорошо удовлетворяют функциям (3) и (4), которые с высокой точностью описывают подавляющее большинство полученных с помощью МКЭ результатов другими авторами, в том числе и для многих пластинок с острыми углами.
0.00175
0.00125
0.00075
0.00025
Анализ линейных функций (3) и (4) показывает, что свободные члены в них на порядок ниже членов, содержащих аргументы. Пренебрегая этими членами, после некоторой корректировки коэффициентов пропорциональности 6, можно записать:
w0 = 1,5965-^^ = 1,5965 Г2 , т о- т
™ = 7’2 = 0,6264-w0, or q где Т - период свободных колебаний пластинок. Расчеты, проведенные по этим формулам, показывают, что получаемые результаты отличаются от соответствующих решений, найденных по формулам (3) и (4), с погрешностью, не превышающей одного процента.
Таким образом, с помощью численного эксперимента показана линейная функциональная связь максимального прогиба пластинок в виде равнобедренного треугольника с произвольными граничными условиями, находящимися под действием равномерно распределенной нагрузки, и квадрата периода их колебаний в ненагруженном состоянии. Эта функциональная зависимость может найти широкое применение в теории моделирования строительных конструкций, а также при разработке методов контроля их жёсткости с использованием вибрационных методов.
1/<о2 ‘
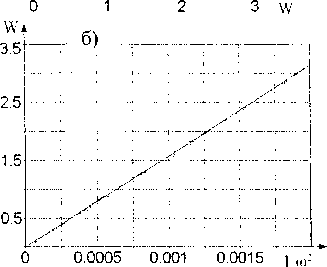
Зависимость максимального прогиба треугольных пластинок от основной частоты их колебаний и наоборот
Список литературы Взаимосвязь задач поперечного изгиба и свободных колебаний треугольных пластинок
- Тимошенко, С.П. Пластинки и оболочки/С.П. Тимошенко, С. Войновский-Кригер. -М. 1963. -635 с.
- Филиппов, А.П. Колебания механических систем/А.П. Филиппов. -Киев: Наукова думка, 1965.-716 с.
- Коробко, В.И. Изопериметрический метод в строительной механике: Теоретические основы изопериметрического метода/В.И. Коробко,-М.. Изд-во АСВ, 1997 -390 с. 4.
- Павленко, А.А. Определение основной частоты колебаний пластинок с жестко защемленным контуром//Тез. докл. научно-практ. конф. «Инженерное обеспечение агропромышленного комплекса»/А.А Павленко. -Орел: ОГСХА, 1998. -С.112-115. 5.
- Коробко, А.В. Интегральная характеристика формы в задачах строительной механики/А.В. Коробко, И.Б. Дробин//Изв. вузов. Строительство, 1994.-№4. -С 100-104. 6.
- Гефель, В.В. Развитие и применение МИКФ к решению задач технической теории пластинок, связанных с треугольной областью. Дис... канд. техн. наук/В.В. Гефель. -Орел: ОрелГТУ, 2006.


