Взаимозависимые многоуровневые космические сети: формальная характеристика

Одна из главных причин написания настоящей работы – оценка и сопоставление живучести дробной архитектуры с живучестью традиционного монолитного космического аппарата. Космические аппараты в космических сетях могут иметь различные компоненты из-за фракционирования функциональности, что приводит к неоднородности узлов [1]. Чтобы проиллюстрировать этот момент, рассмотрим простой пример космической сети, состоящей из двух сетевых космических аппаратов, которые могут подключаться к подсистеме телеметрии, отслеживания и команд другого космического аппарата в случае повреждения или отказа его собственной подсистемы те леметрии, отслеживания и ко © А.А. Брусков, 2021

Информационные технологии и оптимизация управления

Брусков Артем Алексеевич преподаватель Технологического университета имени дважды Героя Советского Союза, летчика-космонавта А.А. Леонова (МГОТУ), город Королёв. Сфера научных интересов: системный анализ, управление и обработка информации. Автор 9 опубликованных научных работ.

манд (см. рис. 1). Беспроводная связь в космических сетях обеспечивает новый тип резервирования – функциональный, но не совмещенный – с помощью подсистемы телеметрии, отслеживания и команд между двумя космическими аппаратами в сети [2; 3].

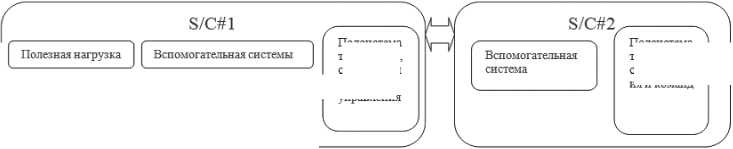
Рис. 1. Упрощенное представление архитектуры космической сети

Каждый космический аппарат состоит из следующих подсистем:

– первый космический аппарат – S/C#1 – содержит все подсистемы, обычно находящиеся в космическом аппарате;

– второй космический аппарат – S/C#2 – состоит из подсистем телеметрии, отслеживания, команд и компонента поддерживающей подсистемы (эквивалентный компоненту в S/C#1). Необходимо обратить внимание, что S/C#2 не имеет компонента полезной нагрузки и рассматривается как резервная копия для подсистемы телеметрии, отслеживания и команд S/C#1.

Неоднородность узлов в космической сети на рисунке 1 не может быть зафиксирована и смоделирована традиционными средствами и представлениями анализа сети.

Цель исследования – разработка концепции взаимозависимых многослойных сетей и ее формальной математической характеристики.

1. Взаимозависимые многоуровневые сети: формальная характеристика

Подсистема телеметрии, отслеживал управления

Подсистема телеметрии, отслеживал ия и команд

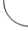
• 1.1.    Общее определение взаимозависимых многоуровневых сетей

На основе концепций взаимозависимости уровней в сети предлагается моделировать сеть с разнородными узлами в качестве взаимозависимой многоуровневой сети.

Представим терминологию, проиллюстрированную общей сетью, изображенной на рисунке 2, с четырьмя гетерогенными узлами, обозначенными Л , Ф , Т и Q с четырьмя возможными функциональными возможностями, обозначенными A , B , C и D .

Суперузел – гетерогенный узел сети, который может иметь различные функциональные возможности. Например, Λ является суперузлом, космический аппарат в космической сети также является суперузлом.

Взаимозависимые многоуровневые космические сети: формальная характеристика

Узел – компонент суперузла, представляющий одну функциональность. Например, окружность, обозначенная как A в Λ , является узлом. Подсистема телеметрии, отслеживания и команд в космической сети также является узлом.

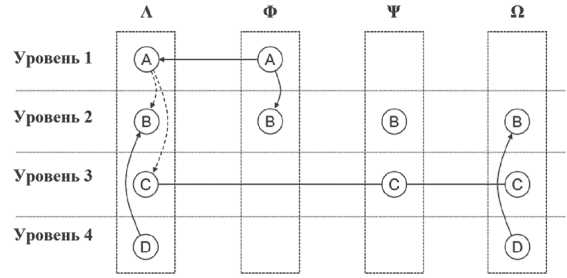
Рис. 2. Общее представление взаимозависимой многоуровневой сети

Слой – общность узлов, имеющих одинаковую функциональность. Все суперузлы в сети и все подсистемы телеметрии, отслеживания команд оставляют уровень, или слой.

Внутриуровневая связь – связь присутствует между двумя узлами на одном уровне, если есть соединение между этими узлами (например, поток данных или узел, который предоставляет ресурсы другому узлу). Линия связи внутри уровня может быть направлена от узла, который предоставляет ресурсы, к узлу-получателю, или может быть в виде двух противоположно направленных дуг, то есть оба узла предоставляют ресурсы другому узлу. Например, у слоя 1 (см. рис. 2) есть направленная связь внутри слоя, указывающая, что суперузел Ф предоставляет функциональность суперузлу Л . У слоя 3 есть две ненаправленных связи внутри слоя между узлами функциональности C (через суперузлы Λ и Ψ и Ψ и Ω). Следует отметить, что на уровне 3 суперузел Λ не предоставляет функции C суперузлу Ω, так как между ними нет явной внутриуровневой связи.

Сетевой слой – слой, имеющий внутриуровневые связи. Например, уровни 1 и 3 являются сетевыми, в то время как уровень 4 таковым не является.

Межуровневая связь – направленная связь, которая фиксирует взаимозависимости между функциональными возможностями в суперузле. В представленной статье взаимозависимость относится к передаче отказа и исследуются два пути распространения отказа – «эффект убийцы» и «эффект предшественника»:

– «эффект убийцы» представляет собой немедленную передачу отказа и символизируется на рисунке 2 сплошной дугой. Например, в суперузле Λ отказ узла, представляющего функциональность D , немедленно приводит к отказу узла, представляющего функциональность B ;

– «эффект предшественника» представляет задержанную передачу отказа и обозначен на рисунке 2 пунктирной дугой.

Например, в суперузле Λ отказ узла, представляющего функциональность A , может привести к отказу узлов, представляющих функциональность B и C , но не является немедленным (условное распространение отказа) (см. рис. 2).

Поскольку узел А в Л соединен с аналогичным узлом в Ф , суперузел Л потеряет функциональность A только в случае отказа обоих узлов или в случае отказа узла в Λ и отказа

Информационные технологии и оптимизация управления внутриуровневой линии связи на уровне 1 между Λ и Ô . В действительности сеть для функциональных возможностей А позволяет выживать суперузлу Λ путем подключения к ресурсам другого суперузла ( Ô ). Следует отметить, что поскольку суперузел Λ не предоставляет ресурсов суперузлу Ô , отказ функциональности A в суперузле Ô немедленно распространяется на узел B через схему эффекта подавления.

Также необходимо отметить, что отказы узлов, представляющих функциональные возможности B и C , не оказывают влияния на другие функциональные возможности. Используемая схема взаимозависимости, аналогична описанному «эффекту убийцы». Однако два эффекта, представленные выше, неисчерпывающие, и другие механизмы каскадного отказа могут быть легко добавлены и реализованы.

Таким образом, представление взаимозависимой многоуровневой сети состоит из узлов, размещенных на нескольких уровнях, представляющих различные типы функциональных возможностей.

В пределах каждого уровня узлы образуют сеть путем соединения с другими узлами с направленными или неориентированными внутриуровневыми связями. Кроме того, межуровневые связи соединяют узлы между слоями для захвата физической реальности суперузлов и моделирования различных типов взаимозависимостей. Представленные в работе взаимозависимости (для анализа живучести) являются двумя примитивами распространения отказа, называемыми здесь «эффектом убийцы» и «эффектом предшественника».

Далее рассмотрим формальную математическую характеристику взаимозависимых многоуровневых сетей.

• 1.2.    Формальное определение взаимозависимых многоуровневых сетей

Основываясь на исследовании [4], взаимозависимую многослойную сеть N можно определить как N(G1,^,GL,Ek,Ep ), где

L-количество уровней каждый из которых пронумерованпоследователъно omldo L G₁,...,G_L -графы на каждом слое VZe[l,..„L],G, = (¥,,£,),где

• У, - множество щ вершин^или узлов)вG_l Е[ - множество рёбер(илизвеньев)в G, Е_к - множество межуровневых рёбер, представляющих «эффект убийцы» Ер - набор межуровневых кромок, представляющих «эффект предшественника»

  
  

Набор сетевых уровней E_R определяется как

E r = { к< I El ^ ^ } (2)

Взаимозависимые многоуровневые космические сети: формальная характеристика

i

Общее число узлов в N равно n =

''n, и узлы пронумерованы однозначно и последо- i=1

вательно от 1 до n . Не имеет значения, какая вершина какую метку получает, важно только то, что каждая метка уникальна, чтобы можно было использовать метки для однозначного обозначения любой вершины [5].

Более практическое представление сети N возможно с помощью:

• 1)    Классических матриц смежности A 1,..., AL для соответствующих графов G 1,..., G_L ;

• 2)    Межслойной матрицы С ;

• 3)    Функции f отображения между двумя схемами нумерации узлов, описанными далее.

Узлы нумеруются от l до n. Данная схема нумерации упоминается в работе как «общая нумерация» и используется как первичная схема нумерации. Вводится дополнительная нумерация узлов для определения матриц смежности, называемая нумерацией слоев: для каждого уровня l узлы нумеруются последовательно от 1 до ni. Функция /отображает метки ко каждого узла в схеме «общая нумерация» в пару целых чисел (l, KL ), где l - номер слоя, а KL - метка узла в нумерации слоя. Обратите внимание, что индексы в схеме «общая нумерация» имеют подстрочный индекс о, в то время как индексы в схеме «нумерация слоев» имеют подстрочный индекс l. Поскольку слои и узлы в обеих схемах пронумерованы однозначно, функция f является биективной. Как следствие, также определя- ется функция обратного отображения / 1.

Для каждого слоя l граф G_L может быть представлен ассоциированной матрицей смежности Al = I al : I так, что

L L-'L J Ui X Ui

l ai • = 1, вели имеется внутриуровневая линия связи,

^

направленная от узла j _L к i_L a l j = 0 - в противном, случае

«Межслойная» матрица C = I c

L * ⁰ j ⁰ J n X n

определяется следующим образом:

Таблица 1

Параметры Вейбулла для времени отказа подсистем космического аппарата в случае подсистемы телеметрии, отслеживания и команд

Функциональность	Параметр формы Вейбулла в	Параметр масштаба Вейбулла и (лет)
Подсистема телеметрии, отслеживания и команд	0,4650	47,770
Поддерживающая подсистема	0,5529	918,5
Полезная нагрузка	0,5921	30,150

Информационные технологии и оптимизация управления

Ci#jo = Еесли имеется ребро от вершиныл() к](р принадлежащее Ек («Эффектубийцы»)

принадлежащееЕк («Эффект предшественника»')

Cjj = Овпротивномслучае

E_k , E_p и E_L также могут быть определены из матриц смежности и межуровневой матрицы следующим образом:

Ek ={( j, г) I cj = 1},

Ep ={( j, i) Icj = 2},

El ={ lIA1 * 0nl x n} .

В заключение отметим, что взаимозависимая многослойная сеть N может быть однозначно определена как N ( G 1,..., GL,Ek,^ap ) или N ( A j , ^ , AL,C, f ) , поскольку две характеристики эквивалентны.

Далее будем использовать оба варианта для рассмотрения некоторых преимуществ последних.

• 1.3.    Иллюстрация взаимозависимых многоуровневых сетей

Предлагаемое представление проиллюстрируем использованием космической сети, представленной на рисунке 1, и ее взаимозависимой многоуровневой сетью, представленной на рисунке 3.

Два космических аппарата являются частью сети и представлены двумя суперузлами. Тремя идентифицированными функциональными возможностями в этом конкретном космической сети являются полезная нагрузка, подсистемы телеметрии, отслеживания и команд, а также вспомогательные подсистемы. Создадим три слоя для представления каждой из этих функциональных возможностей (см. рис. 3). Отказ вспомогательных подсистем ведет к немедленному отказу всего космического аппарата, что, в свою очередь, приводит к недоступности других узлов (подсистемы телеметрии, отслеживания и команд, полезная нагрузка) в различных слоях, принадлежащих этому космическому аппарату. Следовательно, он подпадает под тип взаимозависимости «эффект убийцы» внутри суперузла. Отказ подсистемы телеметрии, отслеживания и команд не обязательно приводит к немедленному отказу космического аппарата [6]. Функциональное резервирование на подсистему телеметрии, отслеживания и команд может обеспечить выживание космического аппарата, если он подключится к подсистеме телеметрии, отслеживания и команд другого космического аппарата [7]. Это возможно, если на уровне подсистемы телеметрии, отслеживания и команд функционирует как связь с другим узлом подсистемы телеметрии, отслеживания и команд, так и этот узел подсистемы телеметрии, отслеживания и команд [8].

Следовательно, отказ узла подсистемы телеметрии, отслеживания и команд подпадает под тип взаимозависимости «эффект предшественника». В результате мы имеем:

• – в случае S/C#1 отказ узла «поддерживающие системы» делает недоступным как узел «подсистемы телеметрии, отслеживания и команд», так и узел «полезная нагрузка» через «эффект убийцы» (см. рис. 3).

Взаимозависимые многоуровневые космические сети: формальная характеристика

– в случае S/C#2 отказ узла «поддерживающие системы» делает недоступным узел «подсистемы телеметрии, отслеживания и команд» через «эффект убийцы». Узел «подсистемы телеметрии, отслеживания и команд» делает недоступным узел «поддерживающие подсистемы» через «эффект предшественника» (см. рис. 3).

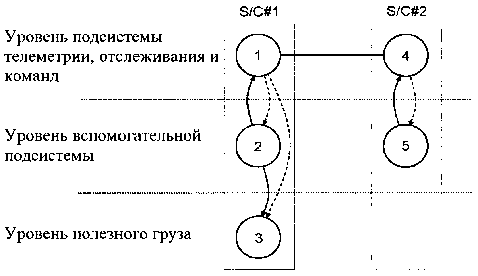
Рис. 3. Взаимозависимое многоуровневое сетевое представление для примера космической сети

Для этого конкретного случая взаимозависимой многоуровневой сетью является

N ( G_vG 2 , G 3 , E_k , E_p ) , где

G 1 = ( V 1 , E1 ) , где V 1 = { 1,4 } и E1 = { ( 1,4 ) , ( 4,1 ) } - граф для уровня подсистемы телеметрии, отслеживания и команд;

G 2 = ( V2,E 2 ) , где V 2 = { 2,5 } и E 2 = 0 - граф для уровня «поддерживающих подсистем»;

G3 = ( V 3 , E3 ) , где V 3 = { 3 } и E 2 =0 - граф для слоя «полезной нагрузки»;

Ek = { ( 2,1 ) , ( 2,3 ) , ( 5,4 ) } ;

^ep = { ( ^1,2 ) , ( 1,³ ) , ( ^4,5 ) } ;

E r = { 1 } , поскольку только уровень 1 имеет внутриуровневые связи.

Альтернативное представление N ( А 1 , А 2 , А 3 , С , f ) примера космической сети приведено следующим образом (см. рис. 4, 5):

A i =

Матрицы смежности A₂ для уровня «поддерживающие подсистемы» (уровень 2 ) и A₃ для уровня «полезная нагрузка» (уровень 3 ) тривиальны, так как в этих уровнях нет внутриуровневых связей:

^A 2 = 0 2 x 2 ^{и A} 3 = ° 1 х 1 -

Межслойная матрица C является следующей:

Информационные технологии и оптимизация управления

	г
	0	1	0	0	0
C =	2	0	0	0	0
	2	1	0	0	0
	0	0	0	0	1
	. 0	0	0	2	0

Общая схема нумерации может быть выбрана для облегчения представления взаимозависимых многоуровневых сетей, в частности межслойной матрицы C. Если общая нумерация выбрана так, что узлы, принадлежащие одному и тому же космическому аппарату, нумеруются последовательно, узлы 1 , 2 и 3 принадлежат S/C#1, а узлы 4 и 5 – S/C#2. Таким образом, межслойная матрица С может быть уменьшена до блочной диагональной формы:

	г
	0	1	0
C =	2	0	00 3 x 2
	2	1	0
			01
	. 0 2 x 3		20

По мере увеличения количества космических аппаратов в космической сети рост межслойной матрицы может быть уменьшен с помощью этой схемы нумерации, поскольку необходимо заполнить только блоки вокруг диагонали [9]. Кроме того, с вычислительной точки зрения это может позволить сохранить матрицу в виде дефицитной матрицы и сохранить память во время моделирования [10, 11].

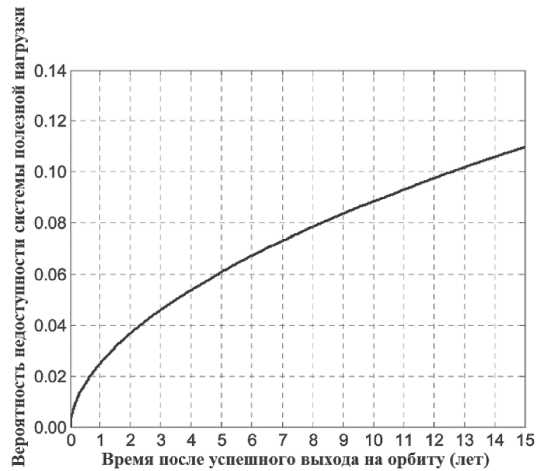
Рис. 4. Выходная вероятность неготовности системы полезной нагрузки с функциональным резервированием подсистемы телеметрии, отслеживания и команд

Взаимозависимые многоуровневые космические сети: формальная характеристика

Традиционная монолитная архитектура:

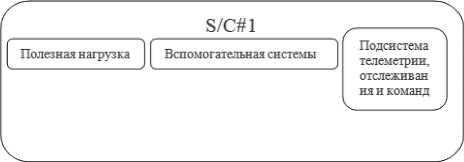
Космическая сеть из двух космических аппаратов:

ня н команд ия и команд

Подсистема телеметрии, отслеживай

Космическая сеть из трех космических аппаратов:

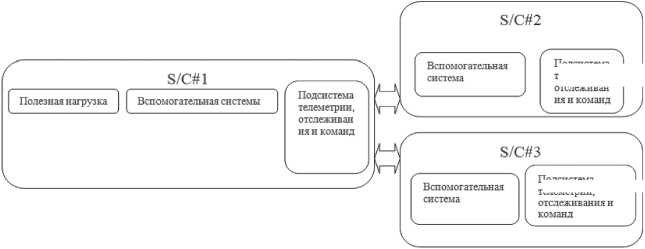
Рис. 5. Космические архитектуры с различными уровнями избыточности подсистемы телеметрии, отслеживания и команд

Наконец, функция f отображения для примера космической сети, задается следующим образом.

– На уровне подсистемы телеметрии, отслеживания и команд, нумерованном уровне 1 , узлу 1 в общей нумерации присваивается номер уровня 1 , в то время как узлу 4 в общей нумерации присваивается номер уровня 2 (рис. 6).

Ниже представлены результаты сравнения вероятностей недоступности системы полезной нагрузки для архитектуры одного, двух и трех космических аппаратов (рис. 7) и график влияния несовершенного беспроводного канала (рис. 8).

– На уровне «вспомогательные подсистемы», нумеруемом уровне 2 , узлу 2 в общей нумерации присваивается номер уровня 1 , в то время как узлу 5 в общей нумерации присваивается номер уровня 2 .

– На уровне «полезная нагрузка», нумерованном уровне 3 , узлу 3 в общей нумерации присваивается номер уровня 1 . Тогда функция отображения f

Подсистема телеметрии, отслеживай

Подсистема телеметрии,

Информационные технологии и оптимизация управления

f ОНм) f ( 2 ) = ( 2,1) b(3)=(3,1) .

f ( 4 ) = ( 1,2 ) . f ( 5 ) = ( 2,2 )

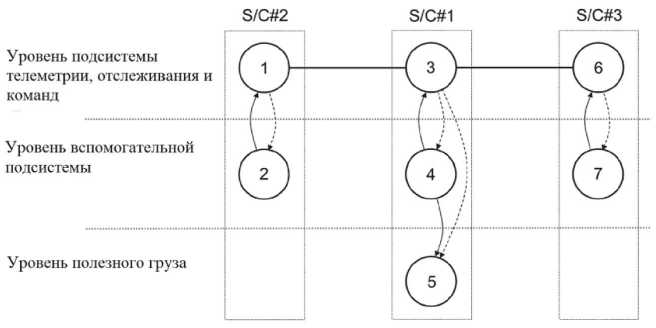
Рис. 6. Взаимозависимое многоуровневое сетевое представление космической сети с 3 космическими аппаратами для функционального резервирования подсистемы телеметрии, отслеживания и команд

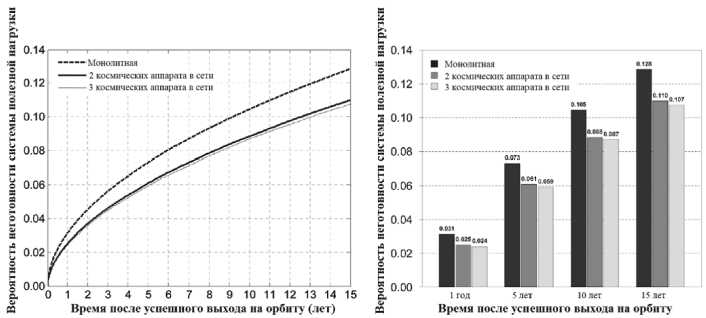
Рис. 7. Сравнение вероятностей недоступности системы полезной нагрузки для архитектуры одного, двух и трех космических аппаратов

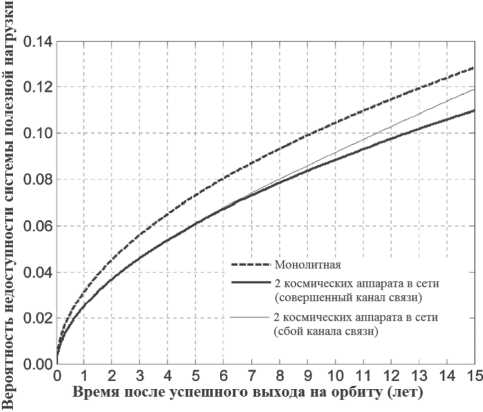
Рис. 8. Влияние несовершенного беспроводного канала

Взаимозависимые многоуровневые космические сети: формальная характеристика

Заключение

Представлен новый подход к определению космических сетей. Исследование мотивировано, с одной стороны, предполагаемыми ограничениями традиционного анализа живучести сети, которые предполагают по большей части однородность узлов (или некоторые вариации одной и той же функции), с другой – растущим интересом к космическим сетям, в которых различные узлы (космические аппараты) могут совместно использовать различные ресурсы на орбите с соседними космическими аппаратами.

Предлагаемый подход основан на идее отображения сети с разнородными узлами во взаимозависимую многоуровневую сеть. Многослойный аспект фиксирует разбивку сети в соответствии с общими функциональными возможностями в различных узлах и допускает появление однородных подсетей, в то время как аспект взаимозависимости ограничивает сеть для захвата физических характеристик каждого узла.

Формальные определения представления взаимозависимой многоуровневой сети были разработаны в поддержку анализа живучести рассматриваемой сети.

Подход и разработанные инструменты могут быть применены в случае космических сетей, которые состоят из нескольких сетевых космических аппаратов, совместно использующих орбитальные ресурсы, – подсистемы телеметрии, отслеживания и команд, центральной вычислительной машины и подсистемы обработки данных.