Wave distribution in stergin under the light of longing foce

When an elastic force acts on an elastic body, various waves propagate through the elastic body, which is not noticeable to us. This paper presents the equation of the longitudinal wave propagation that occurs in a body when a longitudinal force acts on a clamped elastic rod and its solution. The rate of propagation of elastic waves in solids depends on the density and elastic properties of the medium. When elastic waves propagate in the medium, mechanical compression or shear deformations occur, which are transmitted by the wave from one point in the medium to another. Thus, when an elastic body is under the influence of external forces, it has the ability to restore its shape and size on its own after stopping its action. Longitudinal and transverse waves can propagate uniformly in an isotropic solid medium.

REFERENCES AND METHODOLOGY

The effects of external forces on objects have been described in many literatures. However, it is not widely studied today because the wave propagation in elastic bodies under the influence of external forces is not significant, it is difficult to solve the wave propagation equation. [1] in the literature [1], [2], the wave propagation equation are derived using the formulas of the theory of elasticity and many facts about their motion are given.

RESULTS

Calculation of the propagation rate of a longitudinal elastic wave in a solid body in order to come up with the formula, we

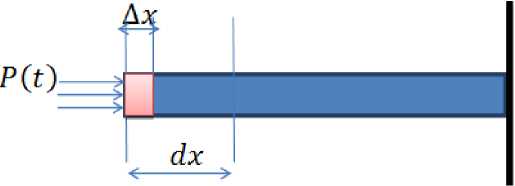
We derive a formula for calculating the velocity of propagation of a longitudinal elastic wave in a rigid body. Suppose that the longitudinal stress P acts on the end of an elastic rod with a cross-sectional area S of time(t). Under the influence of this voltage, the particles of the last layer ∆x move away. The resulting compression deformation is transmitted from layer to layer, forming a longitudinal compression wave that propagates along the rod at time dt and travels a distance dx.

P(t), if t < т 0, if t > т

P(t) = {

The speed (wavelength) of a wave is u:

u = —.(1)

dt

The velocity и of the rod particles is equal to:

u = ^.(2)

dt v 7

If we write Hooke’s law, which represents the deformation of elastic rods:

P(V = E£ = E% = Ed-£.(3)

^v^v

Here is E-Yung module.

We know the tension and the cross- sectional area of the rod.

So, using these, we find the force of elasticity by the following formula:

F_e , = P(t)-S = E-s-S. (4)

According to Newton’s third law, the modulus of external force is equal to the modulus of elastic force.

The external force is equal to the product of the longitudinal force F acting on the impulse dP and the period т of the action.

dP = F-r = P(t) -S-t = E-£-S-t = E~-S-t . (5)

As we know from the course of mechanical mechanics, the following equation holds if a mass object under the action of a force impulse acquires a velocity u:

dP = mu = p • S • dx • и = p • S • dx • ^.   (6)

Where m is the mass of the layer under consideration. Density of .p-stein.

So we equate (5) and (6):

Ax

Ax

E- —- S- r = p- S-dx--

1=^ =v2 V

• (5)    we put (1) and (2) in the formula:

P(t) • т = E • e • т = E ~ • т = E • t^-^ ax          v • at

P(t)-v u =--- E

_       _ P(t)

E

E•p

;   (8)

According to the theory of elasticity, if we write the equation of motion of a binding medium, for a homogeneous rod, it is as follows:

d2w _ dP(t)

^P dt²     dx ’

It this case, the w(x, t) function. ^-W = u, Integrating both sides of this equation by x:

d w      .

so -^— = u is appropriate.

du m^ = P(t)

So if we subtract (8) from (10):

~^— = ^p(i)

We have a differential equation. We integrate this differential equation:

tjEp

2^ .  (13)

P(t) = P0e m

We have a soluition. Now let’s put (3) in (8):

d2w _ ~ d2w     d2w _ E d2w      d2w _

^P dt²       dx²       dt²    p dx²        dt²

The second-order, homogeneous differential equation (narrow oscillation equation) is formed.

So there are several ways to solve the narrow oscillation equation. We solve the problem using the Dalamber method. We need two initial conditioner to solve the initial conditions by putting Ax = w(x, t) in formula (5):

w(x,t)               X P(t)dx

p(t) = ^ = e—— w(x>t) = J —— Ux                   E t/Ё^

w(x, t) = ^^ = p°e m 'x. w(x, 0) = ^ = po(x)(14)

E          EE

^^l   = -^°==p1(x). (15)

dt t=0 JEp P1( )  (

We solve the narrow oscillation equation (13) using the initial condition (14)

and (15) in the Dalamber method. Let’s write the Dalember formula know from the course of mathematical physics equations:

w(x. t) = -[po(x + v • t) + Po(x

^ rX+V't

-vt^ + z^vj    Pi(£^ds

We calculate the know functions p₀(x),p 1 (x) by:

w ...     ^              -

2     E

+

Po'(x- Vt) E

]

+

2 • v

x+v-t x-v-t

P o

J^^P'

ds

w(x. t) = -°-I0    [x + vt — x + vt]+ c

E 2•vJE•p

w(x. t)

Po-x^ Po-t

—F—⁺ i ^{+ c}

^E Je^P

CONCLUSION

In this paper, the longitudinal wave propagation equation generated in a body under the action of a longitudinal force is applied to help a clamped elastic rod and its solution was found in the Dalamber method, one of the ways to solve the wave propagation equation.