Wavelet анализ мощности электромагнитного вибровозбудителя, применяемых в дозаторах-конвейерах

Использование вибрационных принципов при создании машин и освоении рабочих процессов в настоящее время позволяет получать ощутимые результаты. Вибрационные машины, как правило, значительно проще и эффективнее обычных машин, потребляют меньше энергии.

Технологические процессы, осуществляемые с помощью вибрационных воздействие, отличаются высокой интенсивность, ускоренным протеканием процессов, возможностью эффективной переработки многих трудно обрабатываемых продуктов.

Практика показывает, что ряд технологических процессов (просеивание, перемешивание жидких и сыпучих веществ и др.) может быть существенно интенсифицирован с помощью низкочастотного (в диапазоне 1 ÷ 50 Гц) вибро- воздействия с амплитудой колебаний 1 ÷ 10 мм. Простота обслуживания и эксплуатации, высокая долговечность и надежность в самых тяжелых условиях эксплуатации, возможность совмещения транспортных операции с одновременным осуществлением некоторых технологических процедур позволяет выделить электромагнитных вибровозбудителей (ЭВВ) низкочастотных механических колебаний.

В общем случае средняя мощность несинусоидального тока электромагнитного вибровозбудителя (ЭВВ) за период определяется из следующего выражения [1]:

Р = ^£и( )( ((t)d t, (1)

где Р(t) = u(t) ((t) - мгновенная мощность; Т - период, ((t) и u(t) - мгновенные значения тока и напряжения соответственно.

Пользуясь уравнением Хилла мгновенное значение тока представим в виде [2,3,5], где:

( ) = sin(    + ( ) - )ехр     (-

)-      (2  -2 ));(2)

J /

+(  -)

;

=       (       -)

^f^k

()=

---------------------------------\ 2

/    \ 2                / x 2 \

+   -2        (соѕ( -))/

=   ;        =     -

=        ()

Напряжение в цепи ЭВВ представим в виде:

( ) =    ( ) +    ( ) + r( ), где ,    , r – соответственно падение на пряжения в катушке индуктивности, в конденсаторе и в резисторе.

Сетевое напряжение с практически синусоидальной формой кривой опишем в виде: ( ) =    sin(+ )

Если периоды гармонических составляющих ( ) и ( ) имеют наименьшее общее кратное то при выполнении интегрирования в (1) с разбиванием общего интеграла на сумму интегралов, отличным от нуля будет лишь интеграл, содержащий гармоники одинакового периода. Именно наличие последнего характеризует особенности функционирования рассматриваемого ЭВВ механических колебаний.

С учётом (3) мгновенное значение мощности будет:

()   ().

()=  ()+

При этом для средней мощности электромагнитной ЭВВ имеем:

• =  ∫   () + ( )/ ∫  ( )  .  (4)

С целью анализа процесса передачи мощности и оценки соотношения её составляющих проведём исследования правой части (4). Рассмотрим все слагаемые в отдельности.

Для анализа подобных процессов широко применяется преобразование Фурье. Однако с позиции точного представления преобразова- нием Фурье сигналов можно отметить ряд недостатков:

• 1.    Плавная базисная функция, как синусоида не может представлять перепады сигналов с бесконечной крутизной;

• 2.    По составу высших составляющих спектра практически невозможно оценить местоположение особенностей во временной зависимости сигнала и их характер;

• 3.    В условиях практически неизбежного ограничения числа гармоник или спектра колебаний точное восстановление сигнала после прямого и обратного преобразования Фурье практически невозможно, в частности, из-за появления эффекта Гиббса.

Для решения поставленной задачи и получения качественных результатов использован усовершенственный алгоритм Маллата с применением программного пакета Mat Lab 7.

Средняя мощность на участке активного сопротивления определяется следующим выражением:

• =  ∫      ( )   .

С учётом (2) и раскрыв интеграл в правой части этого выражения окончательно получим:

_I 2 _r

^P r = 2 ⁽ q 1 ⁺ q 2 ⁺ ...) ⁺ ...

... + 2 12₀r ( qq eos( -0j -ф ) + ...

nx

... + q^3 eos( -ф — 02 + ~) + ...

... + qq ₄ eos( -ф -0₃ ) + q₂q ₃ eos(0₃ - 0₂ - -) + ...

... + q₂q ₄ eos( 0₁-0₃ ) + ...)                          (5)

где g 1 , g 2 ,... – некоторые коэффициенты, зависящие от z, z p и r .

Полученное выражение (5) показывает, что среди компонент средней мощности на участке активного сопротивления имеются члены, с отрицательным знаком. Это свидетельствует о наличии внутреннего источника в ЭВВ при движении его якоря.

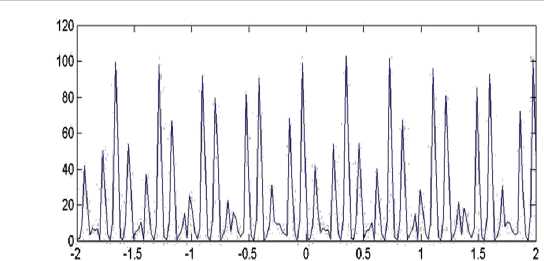
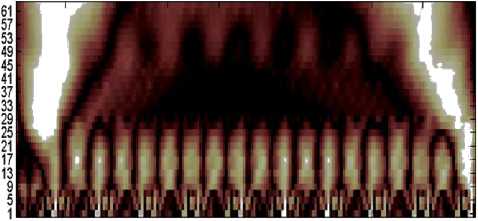
На рис.1 показан вейвлет спектр средней мощности на участке активного сопротивления. Экспериментально и с помощью машинной обработки установлено, что соотношения составляющих для средней мощности на частотах a_K+1,a_K to_K_ 1 составляют 0,54, 1, 0,5

соответственно, т.е. доминирующей является компонента с частотой ю_к , что полностью совпадает с общефизическими законами [4].

g

Ф ( t ) = Ф_м (sin ro_t t +   sin(( to_t - v ) t + 9 ) + ...

Abs. and by scale Values of Ca,b Coefficients for a = 13 5 7 9...

g

... +    sin(( to_t + v ) t + 9 )).

Учитывая (7) в (6), среднюю мощность на участке индуктивности представим в следующей форме:

P l = IW Ф м

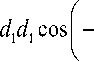
... + dd cos I -9]

+ ...

+ ...

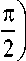
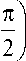
scales a

20       40      60       60      100      120      140     160      160

lime (or space) b

Рисунок 1 – Диаграмма изменения и вейвлетный спектр средней мощности на участке активного сопротивления

I n ... + d.d. cos--- ⁵² I 2

Рассмотрим второе слагаемое в правой

части (4):

TT

P c = _¥ J J i ( t )dt i ( t ) dt .

TC oo

Если учесть, что

T

J i ( t ) dt = 0

o

то имеет место и

P c = 0 ,т.е. полученные результаты для средней

мощности на участке конденсатора подтверждают консервативный характер этого элемен-

та.

Среднюю мощность на участке индук-

тивности представим в виде:

T

T

P l =   1 г Т( Ф ( t)) i ( t ) dt .

T     dt

o

o

Представляя магнитный поток в цепи ЭВВ суммой трёх гармонических составляющих, получим:

... + d₃d cos 9₂ + d₄d cos I 9₃

P + ⁹ 4 l+ ... ,

где d 1 , d 2 ,... - коэффициенты, зависящие от ю_к и V .

По форме полученное выражение соответствует реактивной мощности, и она не равна нулю в силу наличия частотных преобразований в магнитной подсистеме ЭВВ за счёт изменения его электрических и механических параметров.

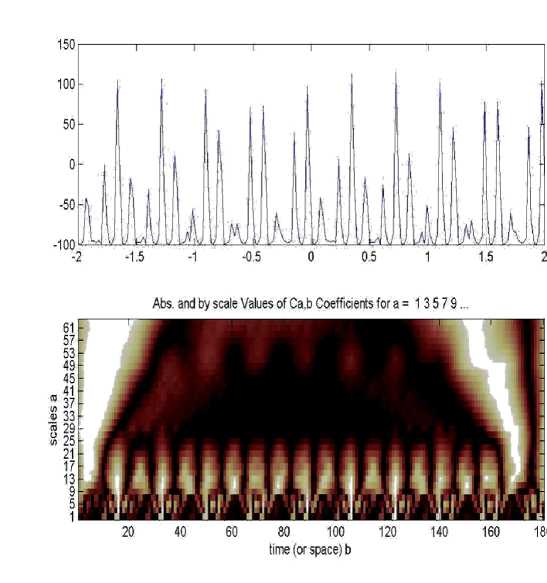
Результаты вычислительного эксперимента показывает, что за счёт частотных преобразований мгновенная мощность на участке индуктивности принимает отрицательные значения, что свидетельствует об эффекте параметрона. Установлено, что соотношения компонент для средней мощности на участке индуктивности на частотах to_K _1 ,to_K,to_K+1 составляют 0,3, 1, 0,18 соответственно (рис. 2).

Анализируя отрицательные компоненты ( g 5 g 6 , g 6 g 9 , d 2 g 6 , ) в правой части выражения (5) и (8), убедимся, что значения этих компонент зависят от вогнутости характеристики L (%), т.е. передаваемая средняя мощность, кроме электрических параметров г, L , С зависят также от механических параметров z , z , , и сис-темы. Оценив и обеспечив рациональное соот-

ношение этих параметров, передаваемую среднюю мощность ЭВВ можно сосредоточить в определённых компонентах.

в 33

Я 29

Abs. and by scale Values of Ca,b Coefficients for a = 1 35 7 9

20       40       60       80      100      120      140      160      181

time (or space) b

Рисунок 2 – Диаграмма изменения и вейвлетный спектр средней мощности на участке индкутивности

ется закону механического движения и зависит как от электрических, так и от механических параметров системы. При увеличении воздушного зазора между магнитопроводом и якорем уменьшается энергия, накопленная в катушке, а в этот момент увеличивается потенциал между обкладками конденсатора. При уменьшении же воздушного зазора происходит обратный процесс [5].

Отметим, что наличие внутренних источников, обусловливающих изменения направления передачи отдельных компонент средней мощности заставляет нас искать причины их существования и пути их преодоления при создании ЭВВ. Без учёта указанных обстоятельств невозможны рациональный расчёт ЭВВ и управление им при эксплуатации. Результаты выполненного исследования могут быть использованы в инженерной практике при проектировании машин.

Обобщая полученные выше результаты, среднюю мощность ЭВВ представим в следующей формуле:

N        Nn

^ [ "T ] = т, I E i [ "T ] r + F EE i [( m - D T - ] +

N V " = 0             C n = 0 m = 0