Wavelet and Blend maps for texture synthesis

Published Online April 2011 in MECS

Textures are extensively used to increase the realism of rendered objects. It is especially important for the realtime rendering of terrain. In this case, the use of large textures often results low performance during rendering. As alternatives, a number of techniques including [Ashikhmin's 2001, Wei and Levoy 2000][1,2], have been developed for procedural texture synthesis. Given a sample texture, these techniques can create a similar texture that fits the target surface naturally and seamlessly. To increase the visual richness of the synthesis texture, blend maps and blending algorithms are used during synthesizing. However, create large blending tiles will consume computation resources and also consume extra texture memory which is very precious now. This paper introduces a method to produce small blend tile which can be tiled together with no seams along the boundaries of two tiles. So the blend tile could be used repeatedly to produce large texture with no need to blend the sharp boundaries. The blend tile is produced by wavelet analysis, so the processing steps and mathematics of our approach are discussed firstly. Advantages of using small blend tiles and its impact on performance are illustrated in the paper.

Related works about texturing terrain or other surfaces using texture tiles and blending technology are discussed in next section, followed by discussion of our

Supported by Scientific Research Common Program of Beijing Municipal

Commission of Education under Grant Nos. KM200710005002o method.

II.    RELATED WORK

In recent years, a great deal of works on texture synthesis based on texture tiles and blending technology has been proposed. Here we simply review some up-to-date and typical approaches.

Texture splatting[3] is the typical technology which use linear blending to smooth the transition between textures tiles and it was used widely in game terrain rendering. The limit of this method is that it needs large alpha maps for blending and linear blending often produced undesirable artifacts.

To improve the quality of synthesis texture, many researchers have contributed their wisdom and effort. [Malik et al.1999][4] proposed conception of texton channel to specify the features of a texture map and the texton map was applied successfully to control procedural texture synthesis by [Zhang et al.2003;Wu and Yu 2004][5,6]. The work of Lai et al.[7] introduced a novel method to blend textures. Their algorithm present identifies the features of an image and provides a visually pleasing border between tiled textures on the terrain. The technology is limited by the number of textures that are precomputed, thus the visual richness of terrain may be reduced. The textures that blend between regions also require extra texture memory, over and above the tiles already in use. Alexandre hardy[8] introduced blend maps to increase the control and observed richness of tiled textures. The technology construct blend map by identifying important features in a texture for these features are often highlighted under certain lighting conditions. The resulting texture produced by the technology appears more realistic in many cases. However, there are too many coefficients need to be define in this method so it is not easy for user.

In our opinion, if the blend map can be tiled seamlessly, the computing work for blending textures will be reduced largely, because there is no need to synthesizing blend map or feature map. So our work is try to produce blend map which can tile together —blend tile with Wavelet analysis.

Our approach is based on the observation that many blend maps, which are Markov Random Field, contains multiresolution signals, that means the map is refinable. While wavelet analysis is a powerful way to analyze and construct functions[9,10,11]. It is therefore natural to use wavelet analysis to process the blend map, remove high frequencies from the map, smooth the remainder. Then the result noise is suitable for tiling and will not cause aliasing and discontinuities.

In the following section we present the overview for processing steps of our approach and the mathematics for deriving this approach is presented in section 4. Practical implementation and results are discussed in section 5.

• I.    OVERVIEW OF OUR ALGORITHM

To provide a context for the remainder of the paper and to simplify the algorithm, we present a high-level overview. The essence of our algorithm consists of the following three steps illustrated in Fig.1:

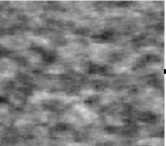
Create the blend map R filled with important features of the textures which suitable for your application.(fig.1a)

Downsample R to create the half-size image

Rd.(fig.1b)

Upsample Rd to a full size image Rn(fig.1c).

Tile Rn to construct large blend map for your application.

Rn is created by downsample R to get the low frequencies and refine it to a full size. Thus Rn contains smoothed low-frequency part of R.

(a)

downsample ►

(b) upsample

(c)

Figure1 ． (a).Blend map R of a texture..(b).Half size image R d . (c).Full size image R n .

III．    THEORY

Wavelet analysis, known as multiresolution analysis, has emerged a powerful way to extract the different frequencies information from original signal and enrich them at the same time. We use this feature of wavelet analysis to process the blend map, and provide the mathematical underpinnings for our algorithm. First, we work in one dimension, then extend to 2 dimensions.

A. Upsampling and Downsampling

In the multiresolution opinion, much function can be represented as a weighted sum of basis function, as following;

F ( x ) = Z f $ (- x -¹ ) (1) i

Where ф (x ) is the basis function and ф (x — I ) is a translated version of ф (x ) by integer amount i. where the f_i are the coefficients of the representation.

If we call the vector space formed by ф (X ) and it’s translated versions the resolution 0 space and denote by S ⁰ :

• 5 0 : ^ F ( x )| F ( x ) = ^ ф (x — i ) > I

  
  

A larger resolution 1 space S ¹ of function can be represented by scaling down the width of ф (x ) by factor of 2. Function G ( x ) in S ¹ take the following form:

• 5    1 ( x ): G ( x ) = £ д ф (2 x — i )             (3)

I

In wavelet analysis idea, all the functions in S⁰ are also in S¹, that means 5 ⁰ C 5 ¹ . This guarantees that S ¹ enriches the space 5 0 . and ф (x ) can be written in terms of ф (2x — k ) :

• ^{ф ( x} ) = E ^h l<Ф^{(2 x — k} )                     (4)

k

Thus given the coefficients f_i that represents F ( x ) in S ⁰ , there exist coefficients f_i ¹ that represents that function exactly in S ¹ :

F ( x ) = ^ f' ^ (2 x - i )                  (5)

I

Using the equation 4 and equation 5, it is straightforward to show that:

• ./ :' = z h - 2 k f k                        (6)

k

The equation 6 represents an upsampling filter, which is in fact used in step 3 of our algorithm.

Although the upsampling filter established above can guarantee that every member of S ⁰ can be represented exactly as a member of S ¹ . The converse is not true: not every function G ( x ) in S ¹ can be represented exactly in the lower resolution space S ⁰ , there is some lost detail. But the loss of detail can be minimized in a least squares sense by wavelet analysis. Assume G ⁰( x ) is the least squares best approximation to

G ( x ) in S ⁰ , then given the coefficients g_i for G ( x ) , the coefficients g_i ⁰ can be determined using standard result from wavelet analysis:

g_i ⁰ = ∑ a_{k - 2 i}g_k                             (7)

k ak is the downsampling filter used in step 2 of our algorithm.

When extend above equation to two dimensions, the 1

upsampling filter f_i represented in equation 6 and downsampling filter g_i ⁰ should be written in the following form respectively:

i,j             i-2kx, j-2ky kx,ky kx,ky

d

RR

Compute ⁿ by upsampling ^d

R

By using equation 12, we get the d containing low frequencies signal represented in S

.

R d looks still rough, not smooth enough.

nd ⁿ

• i ,    j             i - 2 kx , j - 2 ky kx , ky

kx , ky

However,

Thus we

the target rn i, j can be

In this step, no important detail is lost, because all the

R members in d is also represented exactly as members gi, j = ∑ akx-2i,ky-2 j gkx,ky kx,ky

in R n

.

B.    constructing blend tile C.    construct large blend pattern by n In this section, a more detailed algorithm presented in section 2 is described. In our opinion, each blend map can be regard as the function R(x) formed by weighted sum of basis function as equation 1. φ(x) is a wavelet basis function, such as uniform quadratic B-spline basis function, sincs and so on. We use the uniform quadratic B-spline basis function and you can also use other refinable functions, such as sincs, R according to your application. Steps to build n is as following: Create small blend tile R using a texture or other After creating blend tile n , we could define a large R space and tile it with n to create blend map for this space. As illustrated in Fig2. The images on left column are the blend tile processed by wavelet and images on the right column are the blend map tiled by it. The downside method, 1 R={...r ...} such as Perlin noise in S , i, j . Defines function 8: a function R(x, y) in S . Using the basis B(x, y) , R(x, y) can be written as equation R(x, y) = ∑ri,jB(2x-i)B(2y- j) R of using n blend tile is that it will introduce low-frequency repeating patters into the map. Fortunately, this repetition is not always objectionable, In fact, the repetition is beneficial to generate the repeating patter with obvious structures for some applications. For other applications, the repeating pattern can be eliminated by using stochastic function to disturb the signal inner each tile but keep the boundary not change. Only when it needs different tiles in some area, blend method should be adopted to eliminate the discontinuities along the boundaries between different tiles. i,j R Compute d by downsampling As shown in equation 9, R R(x, y) can be a downsampling by downsampling filter   kx,ky to get Rd(x, y) in S0: Rn Rd(x,y)=∑rid,jB(x-i)B(y- j) i,j d And r is computed from the coefficient r : d ri, j = ∑ akx-2i,ky-2 jrkx,ky kx,ky blend map Figure 2．  Create blend map by tiling Rn

• V. IMPLEMENTATION

A Create original blend tiles

There are a numbers of methods for creating original blend tiles. One way is get the blend tile from texture you will use, which will preserved many features of the texture, as shown in fig3. The typical steps are described in alexandre haroy’s paper. Another way is use Perlin noise, which is widely used in texture generating. The advantage of using Perlin noise is that the result image has strong random nature.

B Implementatal Results

The size of blend tile for all examples in our implementation is 128*128, and the size of target blend pattern is 256*256 or 512*512. Fig.3 shows the target patterns generated by blend tiles processed by our method(we name it repeatable noise tile) and Fig.4 shows the blend results of two textures with repeatable blend tile.

When we look at the examples in Fig3, we’ll find that the target patterns generated by original blend tile shows discontinuities on the boundaries of two tiles.

Especially in figure a1,a3and a4, the discontinuities is very obviously. In figure a2, discontinuities is not very intensely. One reasons is that the main part of these blend tile contains high-frequencies noises which result in coarse pattern. And the coarse pattern diminishes discontinuities. The other reason is that the feature of the result pattern makes it difficult to find the discontinuities, such as a2. Use original blend tile to generate large blend map often make the target pattern looks very rough which is not satisfied result for some application, this is in fact the aliasing caused by higher frequencies. So other methods are needed to blend or eliminate the aliasing, but it will consume computation resources and time.

however, use the repeatable blend tile to tile large blend map, the target patterns looks smoothly and there are nearly no discontinuities between two tiles. See b1,b2,b3 and b4 in Fig.3. This shows that our method can make original coarse blend tiles become smooth ， especially the boundary will not contain high frequency nose, thus it is easily use it for realtime texture synthesizing with tiling technology.

C. Advantages discussion

Among the results, the first two original blend tiles, original blend tiles in a1 and a2, are created by textures directly with the method similar to Alexadre hardy [8].original blend tile in a1 are created by texture stone and original blend tile in a2 are created by texture pebble show in fig.4. these two blend tiles all preserve the important features of their textures. With these important features, the target texture will looks more realistic: The grass can’t growth on the pebbles and stone, it should growth around the pebbles and stone, or growth from the cracks. After processed by our algorithm, the result tile still preserves the features of these textures. This is illustrated by blending results in c1 and c2 of Fig4.

The other two original blend tiles are produced by Perlin noise. Perlin noise has been very important for creating textures in computer graphics, for example marble , wood grain and cloud patterns and so on[12,13,14]. But it is hard to use perlin noise tile to accelerate the rendering speed. Because Perlin constructs patterns from bands of noise, that is to say each perlin band is intended to be band-limited, but each band actually contains a much wider ranges of frequencies. These weak band limits lead to some serious problems. Near the Nyquist limit, a Perlin band contains both frequencies that are low enough to be representable and frequencies that are high enough to be unrepresentable. The unrepresentable frequencies will cause aliasing artifacts. These kind aliasing has been a constant source of frustration for shader writer to get satisfied render target. More important, when use perlin noise tile to generate large texture, the aliasing will generate sharp boundary between two tiles in render target(see fig.5).

However, perlin noise is refinable, so we can use wavelet to process it, remove high frequencies from the noise, smooth the remainder. Then the result noise is suitable for tiling and will not cause aliasing and discontinuities, see b3 and b4 in fig.3.

In terrain rendering, many terrain textures are unstructured, stochastic. Thus Perlin noise blend tile will be a powerful way to produce rich ,realistic unstructured terrain textures. In this opinion, our algorithm is a low-cost method to generate unstructured texture. Of course, if need to produce texture with strong random nature, stochastic function may be used to disturb the noise blend tile during blending, this is not difficult to realize.

As for run-time cost for generating large texture pattern, we have not compare our algorithm with other texture synthesizing algorithms, that is our next work. However, because the blend tile is pre-computed and not very large(generally 64*64 or 128*128 is enough), just read from out storage at the beginning of texture creating process, so there is no time-consumption for generating blend tile, at the same time there is no computation consumption for generate large blend map because the blend tile can be used repeatedly. Thus our method is faster than traditional texture synthesizing method based blending. At last but not least, use blend tile will need less memory than previous texture synthesis algorithms. If we textured a large area of terrain with similar appearance constructed by several matters, for example stone, grass and soil. Then only several type small blend tiles are needed. In sum, our algorithm is an effective way to prepare blending data for procedural texture synthesis. In fact, our method cal also be used in any procedural texture generating application with tiling technology.

Original blend tile

Repeatable blend tile blend map

(a1)

(b1)

(a2)                                                                  ^(b2)

(b3)

(a4)

(b3)

Figure 3 ． examples of our algorithm. On the left column (a1,a2,a3,a4)are the original blend tiles and maps tiled by them on the right column (b1,b2,b3,b4)are the repeatable blend tiles produced by our algorithm and result patterns tiled by repeatable blend tiles.

(c1)

(c2)

(c3)

Figure 4 ． blending results of two textures with the repeatable blend tiles produced by our algirithm

(c4)

V. SUMMARY

Our mainly work is processing traditional blend tile by wavelet analysis to generate new blend tile suitable for tiling for large scale texture synthesis. The processing calculation is:

• •    Create a blend tile from a texture or Perlin noise.

• •    Downsampling the blend tile to get a tile of 1/2 size.

• •    Upsampling the 1/2 size tile to new tile of full size.

• •    (Optional)Adjust the tile borders to accommodate tile meshing(if using different tiles).

After processed by above steps, the final blend tile looks smoothly. Use this kind of blend tile to create large blend map, the aliasing and discontinuities along the boundaries is smoothed away and the target pattern become smooth and clear. This means that the blend tile processed by our approach can be used with tiling technology during texture synthesis, which may accelerate the synthesizing speed. although use different tiles to create texture should adopt blending or other technologies to eliminate boundary discontinuities, it is easier to control the final outcome than using traditional blend tiles, because the higher frequencies are eliminated by our processing method. Our next work include using this method for interactive terrain rendering, comparing the performance of our algorithm with other texture synthesizing algorithms, such as Alexadre hardy’ algorithm, and find effective method for transition of different blend tiles