Wavelet Based Intentional Blurring Variance Scheme for Blur Detection in Barcode Images

Published Online May 2014 in MECS

These days’ barcodes are being widely used in trade market [1, 2]. Almost every consumer product has a unique 1-D or 2-D barcode for identification. Barcodes encode a series of characters or symbols to hold explicit information and a database key. With the use of a barcode laser scanner, product information such as manufacturing details and price can be easily accessed. Consumer can obtain information about a product at home or in a supermarket, with a scanning device that can decode the product’s bar code, and a communication device that retrieves the information from a consumer product server. The ease of use of mobile phones with camera facility gives a portable platform for decoding barcode rather than the use of the traditional laser scanner which has lack of portability. Camera phones can take an image of the bar code and after that it can communicate to a consumer product server to access information related with the product. However, using a camera phone in such applications is challenging due to factors such as geometric distortion, noise, and blurring. Image blurring [3, 4] is frequently an issue that affects the performance of a barcode identification system. There are two main kinds of blurring: one is motion blur, which is caused by the relative motion between the camera and object during image capture; the other is defocus blur, which is due to the inaccurate focal length adjustment at the time of image capturing. Blurring induces the degradation of image quality, specifically for barcode images where the encoded information is easily lost due to blur.

An image may be blurred due to diverse sources like atmospheric turbulence, defocused lens, optical abnormality, and spatial and temporal sensor assimilation. Human visual system has good capability to perceive it. However, the mechanism behind this capability is not completely understood for application in artificial visual systems. Therefore, it is hard to design a metric for blur estimation in images. Mean Square Error (MSE), Peak-Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) are few examples of metrics for image quality , but they are by definition based on references, which means that the system needs to have an idea of what an un-blurred image is. We therefore require a mechanism that can detect blur with no use of references. Tong et al. [5] proposed a scheme to decide whether an image is blurred or not and to what extent an image is blurred. They used capability of Harr wavelet transform to discriminate different types of edges and estimate the effect of blur on the edges. Yang et al. [6] addressed the motion blur detection scheme using support vector machine to classify the digital image as blurred or sharp categories. Aizenberg et al. [7] presented a work that considers the blur detection as a pattern classification problem. This work identifies type of blur and estimates blur parameters using neural network for four categories of blur namely defocus, rectangular, motion and Gaussian. Crete et al. [8] used intentional blurring pixel difference (IBD) algorithm due to the fact that it doesn’t require the use of edge detection. Another factor in considering IBD algorithm is its computational speed. As the name states, this algorithm is based on intentional blurring of the given image. The principle stated in [8] is straightforward with the observation that, the intentional blurring of a sharp image gives enormous gray scale variations. On the other hand, intentional blurring of an already blurred image gives small gray scale variations. Although it gives details on calculating the blur estimate, the blur decision threshold is not mentioned. The drawback of the suggested method by the authors is that this method fails to identify blur parameters when the blur size is small.

In this paper, we proposed no-reference blur detection in wavelet domain for barcode images blurred with motion blur, defocus blur and co-existence of both blurs. Automatically determining blurred images helps to apply deconvolution method prior to any further image processing operation. This paper is organized in five sections including the present section. In section 2, we discuss the theory of image restoration and blur models. Section 3 presents barcode segmentation technique. Section 4 gives overview of discrete wavelet transform. Section 5 is devoted to proposed blur detection scheme and section 6 presents experimental results. In the final section 7, conclusion is discussed.

• II.    Image degradation model

The image degradation process can be modelled by the following convolution process as described in [3, 4]

9 ( х , У )= f ( х , У ) ∗ ℎ( х , У )+ Л ( х , У )       (1)

Where, д ( х , У ) is the degraded image in spatial domain, /( х , У ) is the uncorrupted original image in the spatial domain, ℎ( х , У ) is the point spread function that caused the degradation and Л ( х , У ) is the additive noise. Since, convolution in spatial domain is equal to the multiplication in frequency domain, equation (1) can be written as:

G ( и ,v)= F ( и ,V) Н ( и ,V)+ N ( и ,V)       (2)

When the scene to be recorded translates relative to the camera at a constant velocity (v relative ) under an angle of α radians with the horizontal axis during the exposure interval [0, t exposure ], the distortion is one dimensional. Defining the length of motion as L = vrelative × t,exposure, the PSF in spatial domain can be described as [9, 10]:

ℎ( X , У )=

{ 1V√ 0

х² + )/² ≤

Lх

7~ CLTld —=-tanа otherwise

In most cases, the out of focus blur caused by a system with circular aperture can be modeled as a uniform disk with radius R as [11, 12]:

ℎ(1,у)= {лН2           √X2 +

0         otherwise

In the case in which both out-of-focus blur and motion blur are present in the same image, the blur model is:

ℎ( X , У )= а ( х , У ) ∗ Ь ( х , У )          (5)

Where a(x,y), b(x,y) are point spread functions for motion and defocus blur respectively and * is convolution operator.

• III.    Barcode segmentation

  The first step is localization of barcode area in camera based document image. To crop barcode from image we must find two points corresponding to the top-left and bottom-right corner of the barcode area. There exist various approaches for 1-D or 2-D bar code localization using analysis in the spatial domain [13–17], Gabor filtering [18] and analysis in the frequency domain [1920]. We used difference of gradient method [23] for barcode segmentation. The principle behind the approach is that a 1-D barcode consists of vertical bars. Therefore, we may trace the barcode by finding area with high horizontal gradients and low vertical gradients. Based on this idea, we apply following gradient difference operation to an image/( X , У ):

_| G_x |-| G_y | (6)

Where | G_x |and | Gy | are absolute values of gradient in x and y direction. To calculate gradient we used Sobel operator because it has larger convolution mask that smoothes the input image to a greater extent and so makes the operator less sensitive to noise. The Sobel operator [21] computes the gradient by using the discrete differences between the rows and columns of 3x3 neighbourhoods using convolution mask as shown in Fig.1.

-1	0	+1
-2	0	+2
-1	0	+1

+1	+2	+1
0	0	0
-1	-2	-1

^| G_x |                           | Gy |

Fig 1: Sobel convolution masks

So the gradient is computed by the following equations where Z’s are the intensities arranged as in fig.2.

Gx =( Z 7+2 Z 8+ Z 9)–( Z 1+2 Z 2+ Z 3)    (7)

Gy =( Z 3+2 Z 6+ Z 9)–( Z 1+2 Z 4 + Z 7)    (8)

Z1	Z2	Z3
Z4	Z5	Z6
Z7	Z8	Z9

Fig.2: Image neighbourhood

Afterwards, we low-pass filtered the result to eliminate isolated edges and noise. The point where this operation is maximized is assumed to be located within the barcode. From this point, we move outwards to establish precise left and right bounds for the entire barcode. Fig. 3 and 4 shows an image taken by camera and segmented barcode image respectively. This approach gives successful result upto blur extent of 15 pixels.

Fig 3: camera image containing barcode

Fig 4: Segmented barcode image

• IV.    Discrete wavelet transform

The discrete wavelet transform [3, 4] is a dominant and impressionable framework for image processing and analysis tasks. It is broadly used in the fields of image compression, segmentation, de-noising, recognition and fusion etc. The two-dimensional discrete wavelet transform ( DWT ) hierarchically decompose an input image into a sequence of successively lower resolution images and their associated approximate and detail coefficient images. DWT is implemented by a set of filters, which are convolved with the image rows and columns. An image is convolved with low-pass and high-pass filters and the odd samples of the filtered outputs are discarded resulting in down sampling the image by a factor of 2. The l level wavelet decomposition of an image I results in an approximation image Xl and three detail images H,, Vl , and Dl in horizontal, vertical, and diagonal directions respectively. A barcode image contains a pattern of parallel adjacent bars and spaces, which are aligned vertically. Therefore the barcode area should be evidently dominated with vertical textures. So, in the different subbands of the wavelet image, the coefficients of HL subbands from the barcode area are greater than the LH subbands or HH subbands.

• V.    Blur detection scheme

Our algorithm is based on the phenomena of intentional blurring pixel difference (IBD) algorithm proposed by crest et al. [8]. This blur detection scheme works on the principle that it is difficult to observe difference between blurred image and re-blurred version of same image. It can be easily observed that when we blur sharp image there is high loss of details but reblurring of blurred image causes low loss. Fig.5 demonstrates the concept.

Fig 5: (a) Original sharp image, (b) blurred version of (a), (c) reblurred version of (b) with same extent

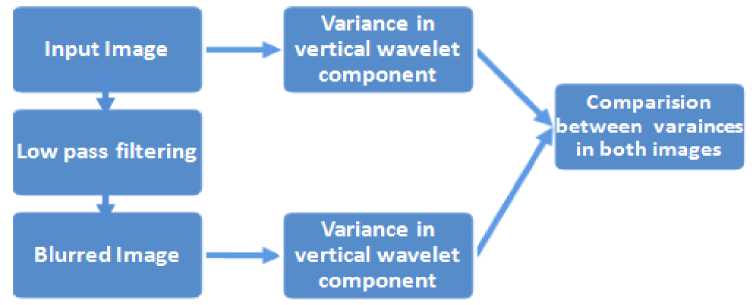
Fig 6: Block diagram of intentional blur algorithm

With the inspiration of intentional blurring scheme, we are able to detect blur on an image by blurring it and comparing the variations in vertical wavelet coefficients before and after the low-pass filtering step. As a result, the first step consists in the estimation of the intensity variations in V l of the input image. On this same image, we apply a low-pass filter and compute variations in V l components. Then, the comparison between these variations allows us to evaluate the blur influence. Thus, a high variation between the original and the blurred image means that the original image was sharp whereas a slight variation between the original and the blurred image means that the original image was already blurred. This description is summarized in Fig.6.

The blur detection algorithm starts by filtering the original image with low pass filter in spatial domain as given in equation (10).

[1  1  1]                (9)

The filtered image is obtained by convolution of input image f(x, y) and filter function h.

b ( x , У )=ℎ ∗ f ( x , У )           (10)

To analyze variance in vertical details of barcode region compute the Haar wavelet transform of input image and blurred image both using equation :

T = (11)

Where F is an Ν Χ Ν image matrix, H is a Ν Χ Ν Haar transformation matrix, and T is the resulting Ν Χ Ν transform. For the Haar transform, H contains the Haar basis functions, hк(z). They are defined over continuous interval z ∈ [0,1] for k=0,1,2,………Ν-1 , where Ν=2^п . To generate H, define the integer k such that k=2р+ԛ-1 , where 0≤р≤n-1 , q=0 or 1 for p=0, and 1≤ԛ≤2р for р≠0. Then the Haar basis functions are:

And

ℎ к ( г )=ℎ pq ( г )

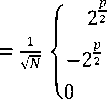
Ч≤z<

2? —2?

9-0 ^․ - ≤ z < 5

2? —2?

Ot ℎ erwise , z ∈ [0,1]

After computing Haar transformation, compute the variance in vertical detail coefficient of input image ( ^) and blurred image ( Vb ) in vertical direction as given below.

Var _ vf =  ∑x=o ( Vf (X,У) - ̅̅̅(̅̅̅,̅̅̅)̅)

Var _ Vb =  ∑x=n ( Vb (X,У)-̅̅̅(̅̅̅̅,̅̅̅))

where,

̅̅̅(̅̅̅,̅̅̅̅) =   ∑ x=o Vf (x,У)

̅̅̅̅(̅̅̅,̅̅̅)= ^ ∑ x=o Vb (x,У)

for X =0,1,…, M -1, and у =0,1,……, N -1 .

In order to analyze the variance of vertical detail coefficients after blurring and compare with the variance of vertical detail coefficients before blurring, variance absolute difference is computed by

Л_Var = max(0, Var_ vf - Var_ Vb)

Then find the sum of coefficients in Var _ Vf and A _ Var as:

5_ Var _ vf =∑y=o VarVf(19)

S_A_Var =∑y=o A_Var(20)

^ℎо =ℎОО ( z )= = , z ∈ [0,1]           (12)

To get final blur factor normalize above sum coefficients using

В F =

sVarv

It is evident that the higher the value of the blur factor (BF), it is more accepted that the input image was blurred.

• VI.    Simulation results

  The performance of the proposed technique has been evaluated using many camera based barcode images. The WWU Muenster Barcode Database [22] of barcode images has been used in order to carry out experimental work. We have taken 100 barcode images. Then, the three different classes of blur (motion, defocus and mixed) were synthetically introduced with different parameters to make the databases of 4000 images (i.e., 1000 images with each class of blur and 1000 without blur). All the algorithms were implemented in MATLAB running on Intel Core2Duo machine with 2.40 GHz processor and 2 GB of RAM memory. The threshold value chosen for blur detection is .4 for both IBD scheme and proposed method.

Table 1: Results

Blur Type	Accuracy (%)
	IBD method [8]	Proposed method
Motion	90.4	96.8
Defocus	99.2	100
Combined	96.2	100
No-Blur	74.4	98.8

Images are contaminated by different types of noise. Most common types of noise are impulsive and Gaussian noise, which affect the image at the time of acquisition due to noisy sensors. Noise also contaminates the image during transmission due to channel errors. Although there are different noise models, this work confines to dealing with blur in the occurrence of Gaussian noise which is the most common scenario in practical applications [3, 4]. The Gaussian noise model is expressed as:

1    - (*2 +У2/ „)

U С^,У) =---2 ^е       '^{2 a}

J J 2-rea2

It is characterized by its variance term o2.

In order to examine the robustness of the proposed method in presence of noise, additive Gaussian noise of 20db SNR is added to create noisy blurred images. Table 2 illustrates the results in presence of noise.

Table2: Results in presence of 20 db noise

Blur Type	Accuracy (%)
	IBD method [8]	Proposed method
Motion	82.2	92.8
Defocus	92.2	94.5
Combined	88.4	95.3
No-Blur	54.4	94.2

The simulation results are listed in table1 and table 2. Results demonstrate the effectiveness of our scheme over proposed by authors in [8] for determining blur. Fig.7 shows few results for blur detection in case of motion blurred, defocus blurred and combined blur in barcode images.

• VII.    Conclusion

In this paper, we have proposed a new blur detection scheme for barcode images taken by digital cameras. The scheme is based on intentional blur variance scheme of wavelet coefficients to discriminate blurred or sharp images. Experimental results show the higher blur detection accuracy compared to the other method without noise as well as in presence of noise. In the proposed algorithm, to achieve good result, threshold has been experimentally set. Automatically determining threshold value needs to further researches.

Acknowledgement

(a) Original Image (No Blur) Blur Factor .0062

(b) Motion Blurred Image

Blur Factor .9912

(c) Defocus Blurred Image Blur Factor .9904

(d) Combined Blurred Image Blur Factor .9958

Fig 7: An example of the proposed scheme to determine the blur factor in different blur categories