Wavelet-NARM Based Sparse Representation for Bio Medical Images

Published Online February 2015 in MECS

Numerous raw images are taken for various applications from cameras/sensors placed on satellites, space probes and aircrafts and bio medical images or pictures taken in normal day to day life. The quality of these raw images has to be enhanced to meet the requirements of the applications they are used into. The quality of an image can be defined by its resolution. Based on number and size of pixels the image is said to be either low resolution (LR) or high resolution (HR) image [1]. In LR image the number of pixels is less and the pixel size is large which results in loss of image sharpness and blurry image. In HR image the number of pixels is more and the pixel size is small, so it results in sharp and finely defined image. The high resolution image (HRI) gives precise details of an image.

The problem of reconstructing HR image from one or more of the LR observations is termed as super resolution. Super resolution image reconstruction offers many solutions to overcome some of low cost imaging sensors limitations and allows the utilization of high definition displays. So this enhancing technology plays very important role in medical imaging and satellite imaging, where analysis of low quality image is extremely difficult. Various techniques have been developed in image processing during the last four to five decades. One of the techniques for converting LR image to HR image is interpolation [2]. The different types of interpolations are nearest neighbour, bilinear and bi-cubic [3, 4]. The main drawback of this method is edge blurring, over smoothening and noise of the image. To rectify this problem, super resolution techniques are used.

Among these super resolution techniques, sparse representation is the best method to give a high quality image. There are many sparse representation models [514]. Here in the algorithm of sparse representation, a LR image is assumed to be an outcome of using a down sampled operator and blurring operator on HR image.

In general the image patches can be well represented as a sparse linear combination of elements from an appropriately chosen over complete dictionary [5]. Sparse representation for each patch of the LR input is estimated and with the coefficients of this representation high resolution output is generated. We can enforce the similarity of sparse representation between the low resolution and high resolution image patch pair with respect to their own dictionaries. Therefore the sparse representation of a low resolution image patch can be applied with the high resolution image patch dictionary to generate high resolution image patch.

But when Dirac delta is used as blurring kernel, i.e. identity matrix is used as blurring operator the whole algorithm gets reduced into an interpolation method [15].

An algorithm is needed to rectify this problem of interpolation method. So NARM method [15] is introduced so as to modify the blurring kernel. The NARM can be embedded into the standard sparse representation model leading to a new data fidelity term and making the sparse representation model (SRM) effective for image interpolation. This further improves the stability and accuracy of sparse coding.

This method when applied to the bio medical images produced unsatisfactory results. In order to improve the resolution of the diagnostic information in the bio medical images, wavelet decomposition is used with NARM. Wavelet transform decomposes the image into scaled components i.e. different sub bands (approximation band, horizontal band, vertical band and diagonal band). In this paper 3-level wavelet decomposition is performed by using Haar wavelet [16]. It produces one approximation band and nine detail sub bands. By making some of the detail sub band coefficients to zero, LR image is reconstructed. To this LR image the NARM based method [15] is applied to obtain the HR image. The performance of wavelet-NARM method is evaluated by mean square error (MSE), root mean square error (RMSE), peak signal to noise ratio (PSNR), mean absolute error (MAE), Pearson correlation co-efficient (PCC), universal quality index (UQI), structural content (STC), and structural similarity index (SSIM) [17], [18]. These values show that the proposed method performs better for biomedical images.

The rest part of the paper is as follows. Proposed method is discussed in Section-II. Results and Conclusions are discussed in Section-III and Section-IV respectively.

• II.    Proposed method

The proposed method for generation of super resolution image is given in Fig.1. The main blocks are wavelet decomposition and NARM.

Image Super Resolution:

Image super resolution aims to reconstruct HR counterpart image from one or several of its LR counterpart. Single image super-resolution can be formulated as

y = DHx + v           (1)

Where, x is the unknown original HR image, h denotes a blurring operator, D denotes down sampling operator, v represents an additive noise, and y is the observed LR data. Reconstructing x from equ.1 is an ill-posed inverse problem. The classical iterative back projection (IBP) algorithm [19] is used to reconstruct x but the reconstructed image is often noisy. So to reduce the computational cost and increase the quality of the image, sparse representation technique is used. In sparse representation model (SRM) the image is represented as sum of weighted coefficients, given by the equ. 2.

x = ya

Where, x is an image, y is the trained dictionary, a is coefficient matrix. The sparse based super-resolution model can be represented as a = argmina {||y-DHya||2 + Xail 1}       (3)

Where, X is constant, || a | is norm of a .

Considering that, the observation is noise free and the blur kernel H is the identity matrix, SRM problem becomes an image interpolation problem which has the disadvantage of edge blurring. To overcome this problem NARM method is introduced [14].

Fig. 1. Block diagram of NARM based method

Nonlocal Autoregressive Modelling (NARM):

Naturally, images have a rich amount of repetitive patterns. For a given unknown image patch, many similar patches which are either close or far to this patch might be found. This type of nonlocal similarity has been effectively used in image de-noising [20-23], de-blurring [24, 25] and super resolution [26, 27]. NARM aims to model a given pixel as the linear combination of its nonlocal neighbouring pixels. It is developed based on the assumption that a given patch can be well approximated by its nonlocal neighbours, which is the basic principle of nonlocal means filtering. To improve the SRM based image interpolation, the nonlocal selfsimilarity constraint is incorporated with the observation model y = Dx in which the canonical sampling matrix D is coherent with the dictionary y making the standard SRM less effective for image interpolation. The missing HR pixel to be reconstructed is denoted as x and calculated as the weighted average of its local neighbour.

The pixel x may have many similar nonlocal neighbours, denoted by x ^j that can be used to approximate x by weighted average.

Wavelet Decomposition

Image transforms are mainly used in image filtering and data description which is used to divide a signal into different scale components. Wavelet decomposition [28] decomposes the image into approximation band and detail bands (horizontal, vertical and diagonal). In level 3 wavelet decomposition different images are constructed by considering different sub-band coefficients and making other sub-band coefficients to zero. The reconstructed images are: R image (reconstructed image by combining all sub band coefficients), RA image (reconstructed by making all other sub band coefficients to zero except level 3 approximation band coefficients), RZ1 image (reconstructed by making level 1 detail sub band coefficients to zero), RZ2 image (reconstructed by making level 2 detail sub band coefficients to zero), RZ3 image (reconstructed by making level 3 detail sub band coefficients to zero), R1 image (reconstructed by making level 2 and level 3 detail sub bands coefficients to zero), R2 image (reconstructed by making level 1 and level 3 detail sub bands coefficients to zero), and R3 image (reconstructed by making level 1 and level 2 detail sub bands coefficients to zero). The detail reconstructed image is shown in Fig.2.

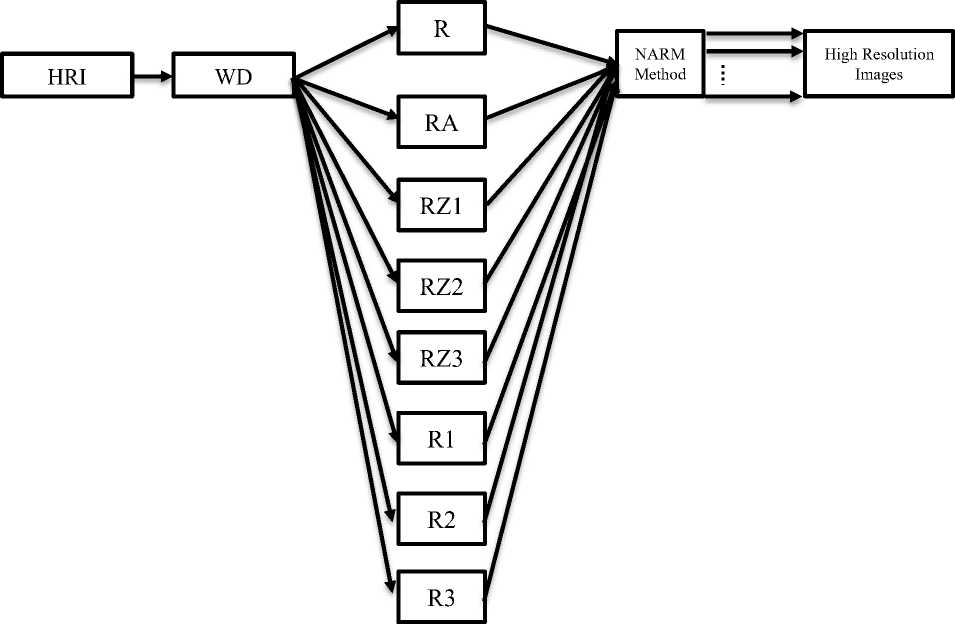
Fig. 2. Block diagram of Wavelet-NARM based sparse representation

In this paper Haar [16] wavelet is used. The Haar wavelet is a series of rescaled square-shaped functions which collectively form a wavelet basis. The analysis of wavelet is similar to Fourier analysis but drawback of this technique is that it is not continuous and therefore not differentiable.

• III.    Results And Discussion

Some high resolution test images are taken to form the database (given in Fig.3). The database consists of Lena, Starfish, Leaves, Parthenon, House, Girl, Foreman, Fence,

Camera Man, and Butterfly images. The high resolution images are first converted into low resolution images and then interpolated method is applied on those images. The resultant images are compared with the high resolution images using performance measures like MSE, PSNR, UQI, SSIM, and STC. The same procedure is followed for the NARM based method also. The resultant performance measures are compared and tabulated in Table.1. For NARM based method the MSE, RMSE, MAE is low as compared to interpolated (bi-cubic) method. PCC, UQI and PSNR for NARM method are high as compared to the interpolated method.

(a)                        (b)                        (c)                        (d)                       (e)

(f)

(g)

(h)

(i)

(j)

Fig. 3. HR images: (a) Lena, (b) Starfish, (c) Leaves, (d) Parthenon, (e) House, (f) Girl, (g) Foreman, (h) Fence, (i) Camera man, and (j) Butterfly

Table 1. Calculation of Performance measures for test images

TEST IMAGES	METHOD	MSE	RMSE	PSNR	MAE	PCC	UQI	STC	SSIM
Butterfly	bic_2	0.004	0.069	71.291	0.034	2.52E+05	0.632	1.004	0.999
	NARM_2	0.001	0.032	77.794	0.016	2.60E+05	0.786	1.002	0.999
Fence	bic_2	0.006	0.078	70.246	0.041	239726.6	0.503	1.002	0.999
	NARM_2	0.003	0.059	72.626	0.033	249361.9	0.634	1.003	0.999
Girl	bic_2	0.001	0.026	79.831	0.017	0.017	0.579	1.013	0.999
	NARM_2	0.000	0.024	80.478	0.016	2.61E+05	0.543	1.004	0.999
Parthenon	bic_2	0.002	0.052	73.796	0.031	2.52E+05	0.619	1.003	0.999
	NARM_2	0.002	0.053	73.590	0.031	2.51E+05	0.593	1.003	0.999
Starfish	bic_2	0.002	0.049	74.358	0.029	2.52E+05	0.707	0.999	0.999
	NARM_2	0.000	0.026	79.585	0.015	2.51E+05	0.834	1.001	0.999
Camera man	bic_2	0.003	0.060	72.507	0.028	2.52E+05	0.469	1.006	0.999
	NARM_2	0.001	0.044	75.191	0.019	2.51E+05	0.591	1.006	0.999
Foreman	bic_2	0.001	0.022	81.219	0.012	2.52E+05	0.621	0.998	0.999
	NARM_2	0.000	0.011	87.178	0.006	2.51E+05	0.724	1.000	0.999
House	bic_2	0.001	0.035	77.056	0.018	2.52E+05	0.466	0.999	0.999
	NARM_2	0.000	0.019	82.413	0.011	2.51E+05	0.565	1.001	0.999
Leaves	bic_2	0.005	0.077	70.406	0.045	2.52E+05	0.619	1.005	0.999
	NARM_2	0.000	0.031	78.191	0.015	2.51E+05	0.817	1.002	0.999
Lena	bic_2	0.001	0.032	78.035	0.018	2.52E+05	0.698	1.001	0.999
	NARM_2	0.000	0.017	83.215	0.009	2.51E+05	0.790	1.001	0.999

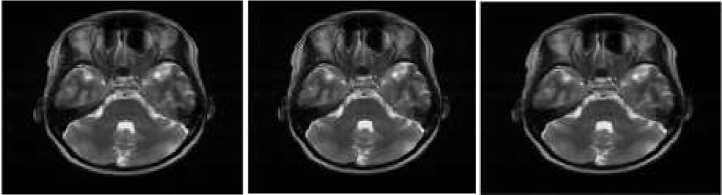
Fig. 4 shows the output of the bi-cubic method and NARM method. Fig. 4(a) is the low resolution image. To this image both interpolated method and NARM based methods are applied. Fig. 4(b) is the output of the bicubic method. In this image the edges are slightly blurred. Fig. 4(c) is the output of the NARM based method. In this image the edges becomes sharp. The output of the NARM based method is almost same to that of the high resolution image given in Fig. 4(d). The results of the above two methods are compared with the original HR image. The NARM method gives better results as compared to bi-cubic interpolation method. The above mentioned methods are applied to the MRI images taken Apollo Hospital, Calcutta. Fig. 5(a) is the MRI Image in which the tumour is represented in the middle of the image. It is white in colour. The tumour is clearly visible in the NARM image as compared to the bi-cubic method. The performance measures are calculated for bi-cubic and NARM based method and tabulated in Table 2. The RMSE, MAE, are less and PCC, SSIM, are found high in NARM method as compared to bi-cubic method.

The NARM based method when used on bio medical images like fundus image, did not produce a satisfactory result. In order to improve the performance of resolution NARM is used on wavelet decomposed image. This method is termed as wavelet-NARM. Wavelet decomposition is applied to the fundus image before applying the NARM. Wavelet decomposition gives rise to approximation coefficients, and detail coefficients (vertical, horizontal, and diagonal coefficients). Further decomposition is achieved by applying decomposition to approximation coefficient. In this case 3-level wavelet decomposition is performed by Haar mother wavelet. Totally 10 bands are generated (nine detail bands and one approximation band).

(a)                           (b)                            (c)                            (d)

Fig. 4. HR image by bi-cubic and NARM method: (a) low resolution image, (b) output image of bi-cubic method, (c) output image of NARM method, (d) high resolution image. The images are cropped to show the differences clearly.

(a)                                    (b)                                    (c)

Fig. 5. Output of bi-cubic and NARM method for MRI images: (a) MRI image of brain, (b) output of bicubic method, and ( c) output of NARM method

Table 2. Calculation of Performance measures for MRI image

TEST IMAGE	MSE	RMSE	PSNR	MAE	PCC	UQI	STC	SSIM
NARM_2	0.000	0.029	78.631	0.007	261534.8	0.822	1.007	0.999
Bi-cubic	0.000	0.030	78.522	0.008	261517.7	0.728	1.003	0.999

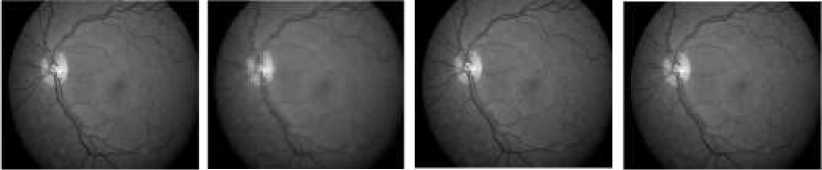
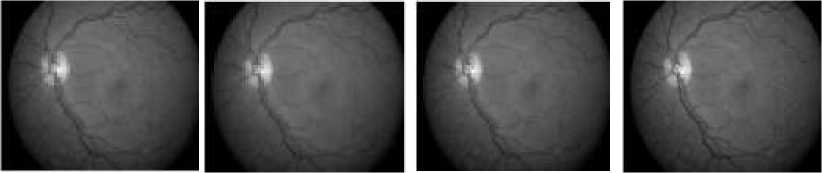
By considering the different band coefficients the images are reconstructed. For example, by considering only the approximation coefficients only and making other coefficients to zero, we obtain the image only due to approximation coefficients only. Similarly we can obtain the reconstructed images by considering the different band coefficients. In this case we have considered eight reconstructed images by combining the different band coefficients. To these reconstructed images NARM method is applied. In these eight images, some contains each and every redundant detail of original image where as others contain the necessary data of the original image, making the data to get compressed. This technique followed by NARM method gave good results in bio medical images. RA is the reconstructed image obtained by considering the approximation band coefficients in level-3. RZ1, RZ2 and RZ3 are the reconstructed image by making level-1, level-2 and level-3 detail coefficients to zero respectively and keeping other band coefficients. R1, R2, R3 are the reconstructed images obtained by keeping level-1, level-2 and level-3 coefficients respectively and making other band coefficients to zero. Fig.6 shows the different reconstructed images obtained after wavelet decomposition. The NARM method is applied to the wavelet decomposed fundus images. Output of the NARM method for different reconstructed images is shown in Fig.7. Performance measures are calculated by comparing the resultant images with the original image and tabulated in Table 3. The same procedure is applied on a set of fundus images and it is found that RZ1 image gives better performance among the set of scaled images by wavelet decomposition. For RZ1 reconstructed image has higher PSNR and UQI values as compared to the other images. From this it may concluded that RZ1 image better for fundus image to obtain the high resolution image.

(a)                               (b)                               (c)                               (d)

(e)                               (f)                               (g)                               (h)

Fig. 6. Reconstructed fundus images after wavelet decomposition: (a) reconstructed image, (b) RA image, (c) RZ1 image, (d) RZ2 image, (e) RZ3 image, (f) R1 image, (g) R2 image, and (h) R3 image

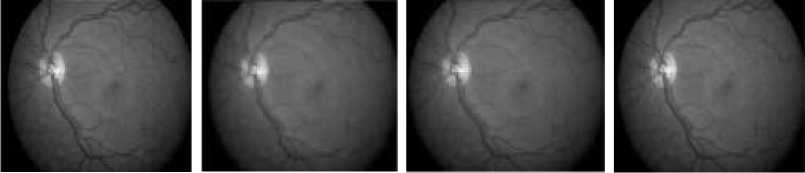
(a)                              (b)                               (c)                              (d)

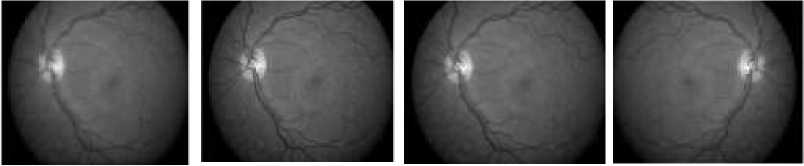
(e)                                 (f)                                  (g)                                 (h)

Fig. 7. Fundus images after using NARM method: (a) R image, (b) R1 image, (c) R2 image, (d) R3 image, (e) RA image, (f) RZ1 image, (g) RZ2 image, (h) RZ3 image

• IV.    Conclusion

In this paper bi-cubic and NARM methods are discussed to obtain the high resolution image. The performance of the high resolution image is studied by different performance measures. From the different performance measure it may be concluded that NARM based method is better as compare to the interpolation method. NARM method also works better for highlighting the exact shape location and boundary of the tumour in the MRI images. The NARM based method fails to find the diagnostic information in the fundus image. To obtain the high resolution image from the fundus image, wavelet decomposition is applied to the fundus image. Here 3-level wavelet decomposition is performed with Haar mother wavelet. The decomposition process give rise to one approximation band at third level and nine detail bands (three at each level). By making the coefficients to zero at each level different images are reconstructed to which bi-cubic and NARM methods are applied. NARM method performs better as compared to bi-cubic method in wavelet bands also. Applying super resolution method on the reconstructed images in wavelet decomposition helps in reducing the computational time as it works in less number of coefficients. NARM based method has given a better performance in different situations and this can be used in medical fields to find the diagnostic information. RZ1 is the reconstructed image obtained by considering approximation band at level-3 and horizontal band, vertical band and diagonal band at level-1. NARM method applied to RZ1 gives higher UQI (0.84) and PSNR (78.61). This method can be further extended for different mother wavelet for specific applications.

• [1]    Rafel C. Gonzalez, Richard E. Woods, “Digital Image Processing,” 3^rd Edition, Prentice Hall publications, 2008.

• [2]    R. G. Keys, “Cubic convolution interpolation for digital image processing,” IEEE Trans. Acoust., Speech, Signal Process., vol. 29, no. 6, pp. 1153–1160, Dec. 1981.

• [3]    H. S. Hou and H. C. Andrews, “Cubic splines for image interpolation and digital filtering,” IEEE Trans. Acoust., Speech, Signal Process., vol. 26, no. 6, pp. 508–517, Dec. 1978.

• [4]    X. Zhang and X. Wu, “Image interpolation by adaptive 2D autoregressive modeling and soft-decision estimation,” IEEE Trans. Image Process., vol. 17, no. 6, pp. 887–896, Jun. 2008.

• [5]    J. Yang, J. Wright, T. Huang, and Y. Ma, “Image superresolution via sparse representation,” IEEE Trans. Image Process., vol. 19, no. 11, pp. 2861–2873, Nov. 2010.

• [6]    W. Dong, L. Zhang, G. Shi, and X. Wu, “Image de blurring and super resolution by adaptive sparse domain selection and adaptive regularization,” IEEE Trans. Image Process., vol. 20, no. 7, pp. 1838–1857, Jul. 2011.

• [7]    Jian Zhanga, Chen Zhaob, Ruiqin Xiongb, Siwei Mab, Debin Zhaoa “Image Super-Resolution via DualDictionary Learning And Sparse Representation,” in IEEE International Symposium on Circuits and Systems (ISCAS), 2012.

• [8]    A. M. Bruckstein, D. L. Donoho, and M. Elad, “From sparse solutions of systems of equations to sparse modeling of signals and images,” SIAM Rev., vol. 51, no. 1, pp. 34–81, Feb. 2009.

• [9]    E. Candès, M. B. Wakin, and S. P. Boyd, “Enhancing sparsity by reweighted L1 minimization,” J. Fourier Anal. Appl., vol. 14, no. 5, pp. 877–905, 2008.

• [10]    M. Elad, M. A. T. Figueiredo, and Y. Ma, “On the role of sparse and redundant representations in image processing,” Proc. IEEE, vol. 98, no. 6, pp. 972–982, Jun. 2010.

• [11]    R. Rubinstein, A. M. Bruckstein, and M. Elad, “Dictionaries for sparse representation modeling,” Proc. IEEE, vol. 98, no. 6, pp. 1045–1057, Jun. 2010.

• [12]    E. Candès, J. Romberg, and T. Tao, “Robust uncertainty principles:  Exact signal reconstruction from highly

  incomplete frequency information,” IEEE Trans. Inf. Theory, vol. 52, no. 2, pp. 489–509, Feb. 2006.

• [13]    E. Candès and T. Tao, “Near optimal signal recovery from random projections: Universal encoding strategies?” IEEE Trans. Inf. Theory, vol. 52, no. 12, pp. 5406–5425, Dec. 2006.

• [14]    J. Mairal, F. Bach, J. Ponce, G. Sapiro, and A. Zisserman, “Non-local sparse models for image restoration,” in Proc. IEEE Int. Conf. Comput. Vision, Tokyo, Japan, Sep. 2009, pp. 2272–2279.

• [15]    Weisheng Dong, Lei Zhang, Rastislav Lukac, Guangming Shi, “Sparse Representation Based Image Interpolation With Nonlocal Autoregressive Modeling,” in IEEE Transactions On Image Processing, Vol. 22, No. 4, April 2013.

• [16]    Piotr Porwik, Agnieszka Lisowska, “The Haar–Wavelet Transform in Digital Image Processing: Its Status and Achievements”, by Machine GRAPHICS & VISION vol.13, 2004, pp .79-98.

• [17]    Kyle Nelson, Asim Bhatti, Saeid Nahavandi “Performance Evaluation of Multi Frame Super Resolution Algorithms” in International Conference on Digital Image Computing Techniques and Applications (DICTA), 2012.

• [18]    Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: From error measurement to structural similarity,” IEEE Trans. Image Process., vol. 3, no. 4, pp. 600–612, Apr. 2004.

• [19]    M. Irani and S. Peleg, “Motion analysis for image enhancement: Resolution, occlusion, and transparency,” J.

Visual Commun. Image Represent., vol. 4, no. 4, pp. 324– 335, Dec. 1993.

• [20]    A. Buades, B. Coll, and J. M. Morel, “A non-local algorithm for image denoising,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2005, pp. 60–65.

• [21]    A. Buades, B. Coll, and J. M. Morel, “Nonlocal image and movie denoising,” Int. J. Comput. Vis., vol. 76, no. 2, pp. 123–139, 2008.

• [22]    K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, “Image denoising by sparse 3-D transform-domain collaborative filtering,” IEEE Trans. Image Process., vol. 16, no. 8, pp. 2080–2095, Aug. 2007.

• [23]    L. Zhang, W. Dong, D. Zhang, and G. Shi, “Two-stage image denoising by principal component analysis with local pixel grouping,” Pattern Recognit., vol. 43, pp. 1531–1549, Apr. 2010.

• [24]    S. Kindermann, S. Osher, and P. W. Jones, “Deblurring and denoising of images by nonlocal functionals,” Multisc. Model. Simul., vol. 4, no. 4, pp. 1091–1115, 2005.

• [25]    X. Zhang, M. Burger, X. Bresson, and S. Osher, “Bregmanized nonlocal regularization for deconvolution and sparse reconstruction,” Dept. Math., UCLA, Los Angeles, Tech. Rep. 09-03, 2009.

• [26]    M. Protter, M. Elad, H. Takeda, and P. Milanfar, “Generalizing the nonlocal-means to super-resolution reconstruction,” IEEE Trans. Image Process., vol. 18, no. 1, pp. 36–51, Jan. 2009.

• [27]    W. Dong, G. Shi, L. Zhang, and X. Wu, “Super-resolution with nonlocal regularized sparse representation,” Proc. SPIE Visual Commun. Image Process., vol. 7744, p. 77440H, Jul. 2010.

• [28]    Michael Elad “Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing”, Springer, ISBN 978-1-4419-7010-7.