WGEP — новый способ противодействия перекрёстным членам в преобразовании Вигнера — Вилля

Обработка сигналов – крайне важная составляющая процесса вибродиагностики вне зависимости от того, работает с сигналами человек или нейронная сеть. Преобразование сигналов позволяет получить так называемую спектрограмму (или скалограмму, если используется Вейвлет-преобразование), которая позволяет легче определять признаки сигналов и их поведение во времени.

Существует много методов преобразования сигналов, каждый из которых подходит под свою задачу в зависимости от его скорости работы, разрешения во временном и частотном диапазонах и артефактов. При работе с нейронными сетями особое внимание уделяется борьбе с артефактами, чтобы на вход нейронной сети подавались как можно более точные данные.

В статье предлагается метод борьбы с артефактами, присущими методу PWVD, WGEP, разработанный в процессе использования на практике другого метода сглаживания, известного как EMD PWVD, который и лег в основу WGEP.

Почему EMD PWVD

Для работы с непрерывными сигналами требуются методы обработки, алгоритм работы которых отличается быстротой, но поскольку интерпретировать результаты согласно изначальной концепции должна нейронная сеть, результаты, как уже было сказано, также должны быть четкими и наглядными, чтобы упростить поиск признаков сигналов. Такие общеизвестные методы, как кратковременное преобразование Фурье (далее – КВПФ) и вейвлет-преобразование, конечно, обладают большой скоростью, однако их разрешение в частотно-временной области сильно зависит от таких факторов, как длина оконной функции или частота, на которой идет обработка сигнала.

В процессе поиска методов преобразования сигналов для производительной и качественной обработки непрерывных виброакустических сигналов с целью их дальнейшей подачи в нейронную сеть, классифицирующую дефекты технологического оборудования, было обращено внимание на метод преобразования Вигнера – Вилля (англ. Wigner – Ville Distribution) благодаря его высокому разрешению как в частотном, так и временном диапазоне.

К главным недостаткам данного метода можно отнести его артефакты – перекрестные члены (англ. cross terms), являющиеся следствием билинейности PWVD [1]. Среди методов борьбы с ними особое внимание получил метод EMD PWVD, соединяющий в себе разложение сигнала на внутренние моды и псевдопреобразование Вигнера – Вилля. Алгоритм реализации EMD PVWD довольно прост. Он заключается в разбиении сигнала на внутренние моды (IMF), к которым затем применяется метод PWVD. Результаты преобразования накладываются друг на друга в результирующий массив данных [2].

Применение упрощенной формы EMD PWVD

Поскольку, как было сказано выше, метод обработки непрерывных сигналов должен отличаться скоростью вычислений, при первой попытке применения EMD PWVD в качестве эксперимента вышеупомянутый метод был реализован в своей максимально упрощенной форме – согласно своему описанию в статье создателя EMD PWVD Хонгвея Фана [2].

Однако проведенные эксперименты по использованию «упрощенного» EMD PWVD не принесли желаемых результатов, так как артефакты, называемые «перекрестными членами», не исчезли с итоговой спектрограммы (см. Рисунок 1).

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год

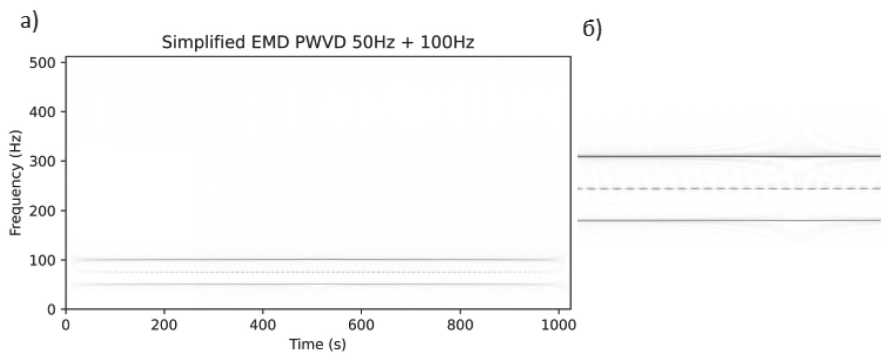
Рисунок 1. Результат преобразования сигнала из двух синусоид 50 и 100 Гц при помощи EMD PWVD ( а ); приближенный фрагмент графика ( б ): заметны перекрестные члены в виде пунктирной линии посередине

Источник: здесь и далее рисунки выполнены авторами.

Исследования показали, что корректная реализация метода EMD PWVD несколько сложнее, чем кажется на первый взгляд, что привело к идее разработки метода, учитывающего главную идею простого в реализации EMD PWVD-преобразования сигнала по его внутренним модам.

Фильтр Гаусса

Идея применения фильтра Гаусса для борьбы с перекрестными членами берет свое начало из метода сглаживания, предложенного Люком Кустерсом в библиотеке для языка Python – Wigner DPY1. Он, в свою очередь, основывался на методе, предложенном в статье [3]. Основная идея состояла в попытке сгладить перекрестные члены сигнала в расчете на то, что они исчезнут или станут менее заметными.

В результате применения фильтра Гаусса перекрестные члены между линиями 50 и 100 Гц исчезли, однако разрешение в частотном диапазоне сильно упало, что можно увидеть в «размытом» изображении линий в частотном диапазоне. К тому же амплитуда сигнала на 50 Гц заметно ниже амплитуды на 100 Гц, хотя в изначальном сигнале они одинаковые (см. Рисунок 2).

Также при добавлении нового сигнала с частотой в 75 Гц из-за близкого расположения линий между ними возникают артефакты. Одного фильтра Гаусса явно недостаточно, что, в свою очередь, подводит к следующему шагу (см. Рисунок 3).

WGEP – новый способ противодействия перекрестным членам в преобразовании

Вигнера – Вилля

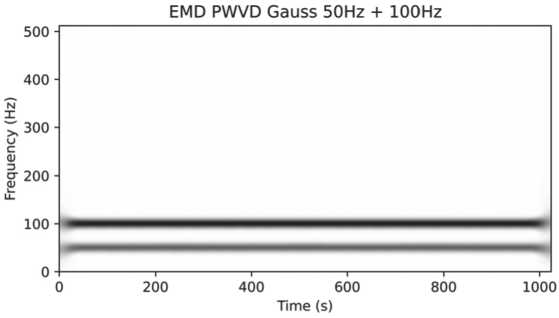
Рисунок 2. Результат преобразования сигнала из двух синусоид 50 и 100 Гц при помощи EMD PWVD с фильтром Гаусса: перекрестные члены исчезли, значение среднеквадратического отклонения (σ) равно 12

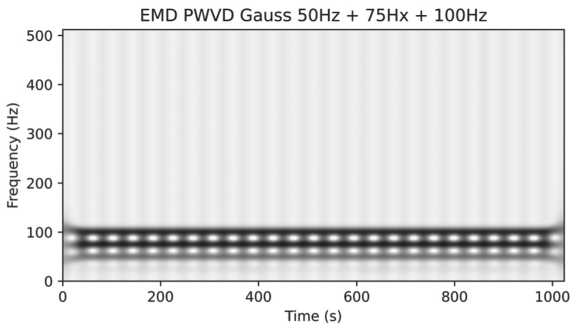
Рисунок 3. Р езультат преобразования сигнала из трех синусоид 50, 75 и 100 Гц при помощи EMD PWVD с фильтром Гаусса. Видны множественные артефакты

Коэффициент средних энергий

Поскольку, как показано ранее, низкие частоты теряют в амплитуде, было проведено умножение каждой строки спектрограммы на некий коэффициент, соответствующий частному между средней энергией частоты до фильтра Гаусса и после него. К тому же умножение на коэффициент должно было вернуть четкость сигнала на нужной частоте, потерянную при сглаживании. В результате сигнал не только стал четким, но и почти полностью лишился перекрестных членов. Лишь при очень сильном приближении можно заметить крайне неяркую линию ниже 50 Гц на Рисунке 5.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год

б)

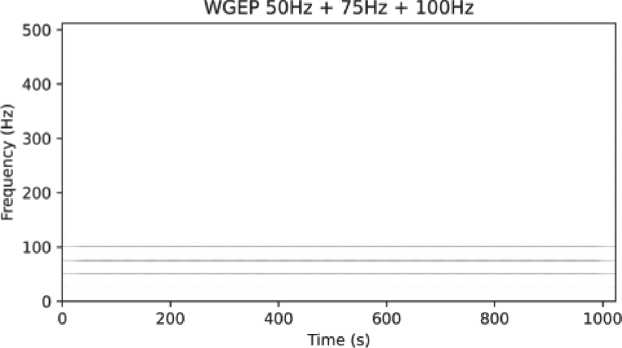
Рисунок 4. Результат преобразования сигнала из трех синусоид 50, 75 и 100 Гц при помощи EMD PWVD с фильтром Гаусса и умножением на коэффициент ( а ); приближенный фрагмент графика ( б ): артефакты исчезли

0          200

Рисунок 5. Приближенное изображение спектрограмммы.

Видна неяркая линия ниже 50 Гц (4-я сверху)

Итоговый алгоритм метода выглядит следующим образом.

• 1.    Разбить сигнал на внутренние моды, получив n внутренних мод.

• 2.    Провести PWVD над внутренней модой i , пока i <  n , получив массив PWVDi.

• 3.    Высчитать среднюю (или суммарную) энергию ei для каждой частоты PWVDi.

• 4.    Применить фильтр Гаусса над PWVDi, получив PWVD_Gi.

• 5.    Высчитать среднюю (или суммарную) энергию egi для каждой частоты PWVD_Gi.

• 6.    Определить коэффициент k как частное от деления ei на egi, избегая деления на ноль.

• 7.    Домножить PWVD_Gi на k, получив взвешенный результат PWVD_G_Wi.

• 8.    Суммировать PWVD_G_Wi с результирующим массивом PWVDr.

• 9.    Увеличить i на единицу и перейти к шагу 2.

Также можно после окончания цикла умножить результирующий массив на средний коэффициент для каждой частоты, что позволит несколько уравнять амплитуды сигналов на высоких и низких частотах.

WGEP – новый способ противодействия перекрестным членам в преобразовании

Вигнера – Вилля

В силу природы метода и использовавшихся для его реализации шагов его можно обозначать как WGEP (Weighted Gaussian EMD PWVD, или взвешенное Гауссово преобразование Вигнера – Вилля внутренних мод).

Перекрестные эксперименты

Для подтверждения того, что положительный результат стал итогом применения основной концепции EMD PWVD, были проведены тесты, в которых вышеупомянутый метод сглаживания применялся при простом PWVD без разбиения сигнала на внутренние моды. Эксперименты показали, что данный метод сглаживания борется с перекрестными членами, только если изначальный сигнал разбит на внутренние моды, как в методе EMD PWVD.

На Рисунках 6 и 7 показан результат преобразования сложного сигнала без разбиения и с разбиением на внутренние моды соответственно. Сигнал состоит из нескольких синусоид (50, 75, 100 и 300 Гц), причем некоторые из них прерываются от одного (100 и 300 Гц) до нескольких (50 Гц) раз.

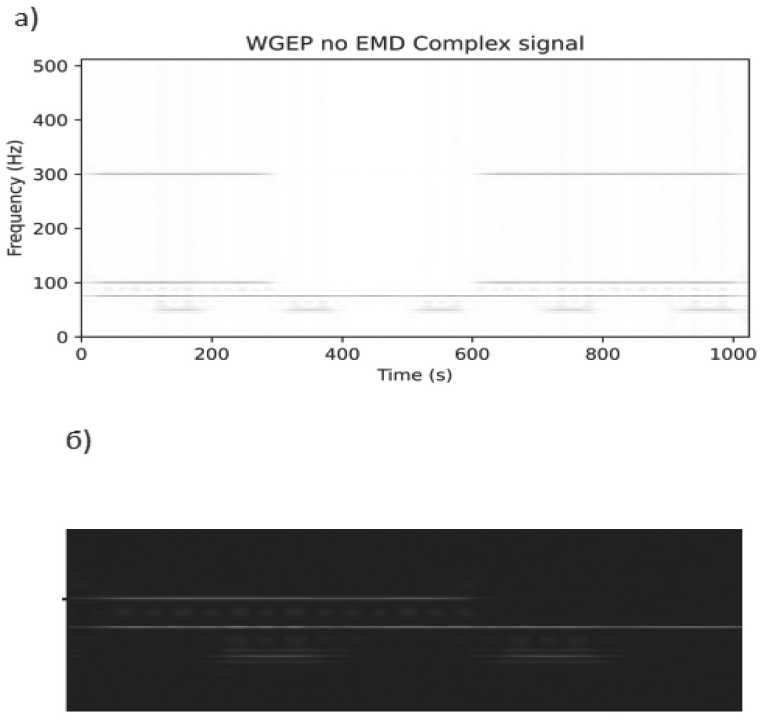
Рисунок 6. Результат преобразования сложного сигнала из нескольких синусоид при применении фильтра Гаусса и коэффициента без разбиения на IMF ( а ); приближенный фрагмент спектрограммы (цвета инвертированы) ( б ). Видны множественные артефакты в виде размытых пунктирных линий (2-я и 4-я сверху)

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год

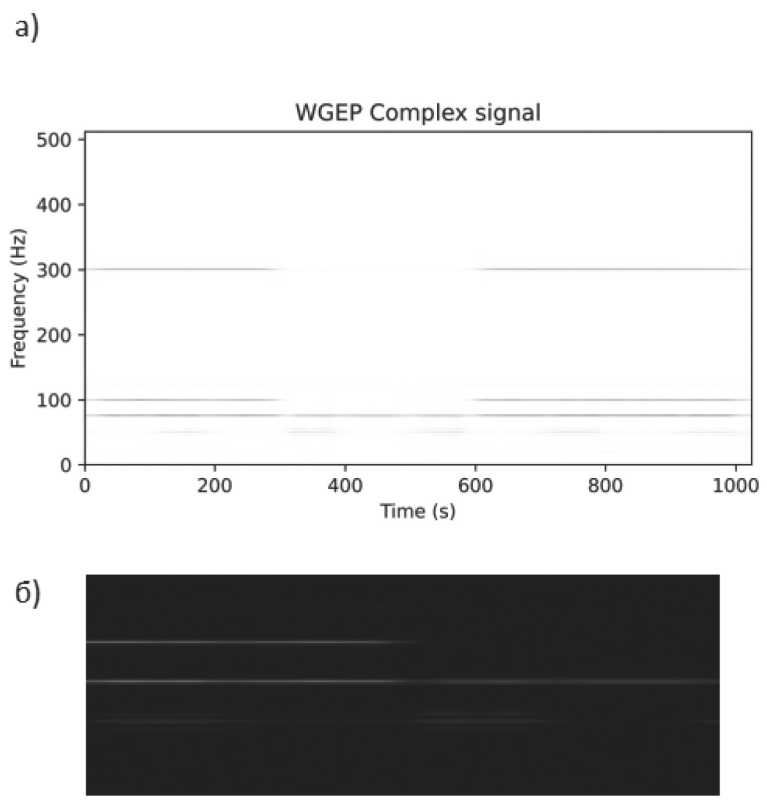
Рисунок 7. Результат преобразования сложного сигнала из нескольких синусоид при помощи WGEP ( а ); приближенный фрагмент спектрограммы, аналогичный фрагменту на Рисунке 6 (цвета инвертированы) ( б ): артефакты практически исчезли

Замеры по времени

Поскольку одним из основных факторов оценки эффективности метода WGEP является скорость работы, было проведено сравнение скоростей со встроенным методом сглаживания библиотеки Wigner DPY. В результате стало ясно, что WGEP выигрывает у встроенного метода. Для этого использовался встроенный функционал генерации сигналов библиотеки Wigner DPY, позволяющий создавать сигналы с требуемой частотой дискретизации и длиной, равной частоте дискретизации. При небольшой длине сигнала (1024 семпла) разница почти незаметна, но при увеличении частоты дискретизации и длины сигнала эффективность WGEP повышается (см. Таблицу).

WGEP – новый способ противодействия перекрестным членам в преобразовании

Вигнера – Вилля

Таблица

Сравнение эффективности WGEP и встроенного метода Wigner DPY

Метод/длина сигнала, семплы, и частота дискретизации, Гц	1024	2048	4096	8192
WGEP	≈ 1,3 с	≈ 6,5 с	≈ 32,2 с	≈ 145,6 с
Wigner DPY	≈ 2,2 с	≈ 17 с	≈ 129,2 с	нехватка ОЗУ, ожидается ≈ 904 с
Сравнительная эффективность	≈ 1,7 с	≈ 2,6 с	≈ 4 с	ожидается ≈ 6,2 с

Источник: таблица составлена авторами.

Можно заметить, что при увеличении длины сигнала в 2 раза время выполнения WGEP увеличивается примерно в 4…5 раз при увеличении времени метода из библиотеки Wigner DPY примерно в 7 раз. Применение сглаженного Wigner DPY над сигналом длиной 8192 семпла было неудачным из-за нехватки ОЗУ, однако можно экстраполировать, что в более благоприятных условиях он бы затратил примерно 904 с, или около 15 минут, в то время как WGEP справился, в отличие от Wigner DPY, с задачей обработки сигнала длиной 8192 семпла примерно за 145 с.

На графике (см. Рисунок 8) по оси Y показана эффективность WGEP по сравнению с методом библиотеки Wigner DPY при разных длинах сигнала, включая длины короче 1024 семплов, не вошедшие в Таблицу. Значение по оси X соответствует множителю числа 1024 (начальная длина сигнала в семплах), Y – эффективность WGEP по сравнению со встроенным методом библиотеки Wigner DPY.

Судя по графику, метод WGEP обеспечивает преимущество примерно со значения 0,33, что соответствует примерной длине сигнала в 338 семплов.

Проведенные исследования позволяют сделать следующие утверждения.

• 1.    Несмотря на то что WGEP успешно борется с артефактами, у него есть ряд недостатков, большей частью происходящих из природы преобразования Вигнера – Вилля. Так, скорость преобразования IMF зависит от длины подаваемого на обработку сигнала (или, применительно к обработке непрерывных сигналов, длины окна). Увеличение длины окна в 2 раза приводит к увеличению времени обработки в 4…5 раз, поэтому в случае работы с непрерывными сигналами следует использовать небольшую длину окна.

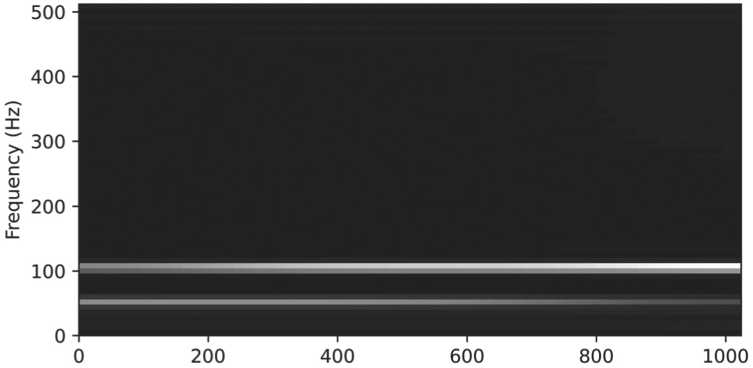
• 2.    Второй недостаток: при использовании небольшой длины окна и высокой частоте дискретизации теряется разрешение в частотном диапазоне, как показано на Рисунке 9.

Эти два недостатка приводят к необходимости находить баланс между длиной окна и скоростью работы метода. Необходимо заметить, что эксперименты проводились с использованием языка Python на стандартном ЦП частотой 3,4 ГГц. Эксперимент, реализованный на более быстром языке программирования и запущенный на более мощном компьютере со специализированным процессором цифровой обработки сигналов, вполне вероятно, сможет показать приемлемую скорость даже при большой длине окна.

Также стоит заметить, что лучше всего этот метод подходит для преобразования таких сигналов, у которых линии частот прерываются как можно реже. На Рисунке 7, б со сложным сигналом можно заметить, что прерывистая линия сигнала на 50 Гц (1-я снизу) сильно проседает в амплитуде и выглядит тусклой по сравнению с другими линиями.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год

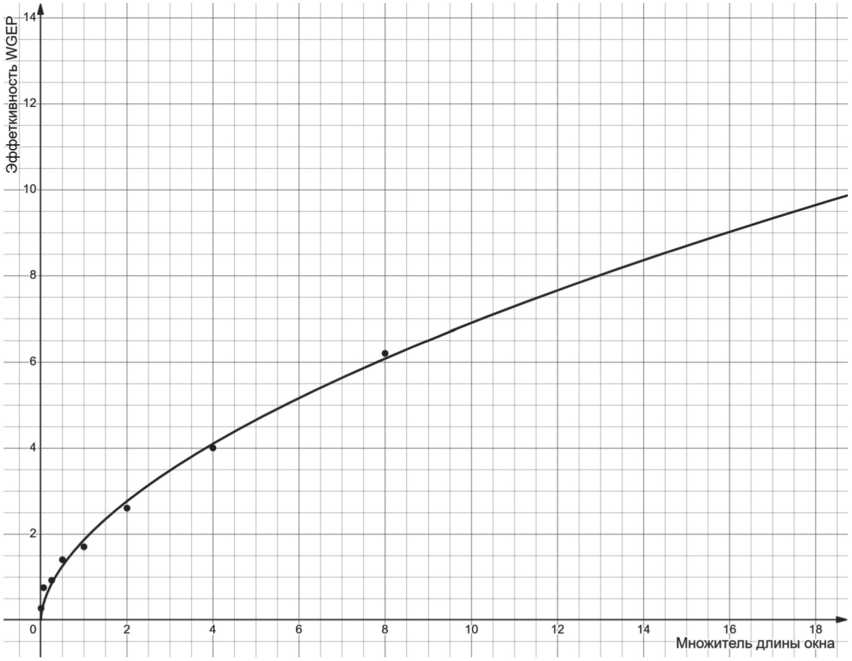
Рисунок 8. График зависимости эффективности WGEP от длины сигнала

64 samples 1024 Hz

Time (s)

Рисунок 9. Спектрограмма сигнала длиной 64 семпла и частотой дискретизации 1024 Гц Заключение

В качестве результата проведенной работы предлагается метод сглаживания перекрестных членов WGEP, отличающийся сравнительной простотой и хорошей скоростью выполнения. И хотя он не лишен недостатков, теоретически он вполне может использо-

WGEP – новый способ противодействия перекрестным членам в преобразовании Вигнера – Вилля ваться при обработке непрерывных сигналов перед их подачей на нейронную сеть. Специализированное оборудование и реализация на более быстром языке программирования также может увеличить его эффективность. Однако для лучшего понимания его рамок целесообразного использования и возможностей, а также для практического использования в обработке непрерывных сигналов требуются дальнейшие исследования.

Поскольку изначальная концепция применения EMD PWVD, приведшая к разработке WGEP, подразумевала его работу в процессе вибродиагностики технологического оборудования при помощи нейронных сетей, целесообразно связывать дальнейшие исследования именно с этой областью, однако WGEP вполне может применяться и в смежных областях.