WOA Enabled Fuzzy-C-Means Segmentation for Accurate Detection of Polycystic Kidney Disease

Polycystic Kidney disease (PKD) affects the kidney and lead to complications and hospitalization. PKD forms several cyst clusters, which happens a kidney to enlarge and lose over function in due time. The symptoms are high blood pressure and back pain. It is an inherited disease which involves bilateral kidneys. PKD should be identified in earlier stage, because symptoms may not visibly appear until late stages of cyst development. Radiological imaging method like Magnetic Resonance Imaging (MRI) of the patient is used to detect and diagnose the PKD. PKD is categorized into two major classifications such as Autosomal dominant PKD (ADPKD) and Autosomal recessive PKD (ARPKD). ADPKD patients affected but not that much of ARPKD They lead a normal life; conversely, ARPKD can cause kidney dysfunction and leads to kidney failure. The removal cyst is the remedial measure to reduce the rigorousness of the disease. The early detection of a disease is based on the accurate segmentation of MRI probe. Although many algorithms are proposed to solve the medical imaging segmentation, but still it remains a challenging task in computer vision. Unified framework for achieving fast image segmentation is still in research. There are two reasons for the difficulty in medical image segmentation one is that the medical imaging is a multi-solution problem and another is complexity due to to noising effect and intensity non-uniformity. Renal column, renal cortex, renal medulla and renal pelvis are the major segments to discover the kidney disease. Feature extraction is needed to provide remarkable attributes, histogram characteristics, geometric features and gray level attributes. The probe image segmentation algorithms is constructed on a kernel fuzzy C-means, But the feature based FCM implemented with superpixel information which will improve the efficacy of image segmentation.

There are existing algorithms like FB-K means, IB-FCM and IB-K-Means. Several identification tools are available for imaging analysis such as ITK, FSL, GIMIAS and Elastix etc. The authors in [1] proposed an exacting imaging acquisition system to identify and analyze kidney segmentation based on diverse processing. The authors in [2] suggested a complex valued implied shape model to identify 3D shape model. The model offered anatomical knowledge to the non-medical observers. A fully automatic method is suggested in [3] to identify four distinctive components of kidney. They used modified random forest (MRF) method to segment and analyze through localization phase. An effective model-based methodology is proposed in [4] for segmenting abdominal CT images. Clinical diagnosis and extraction is produced through the location of the spine, elliptic region and adaptive region. In [5] higher end spatial communication is provided to show the regional attributes and tissue classification. .FPGA based CAD system is proposed in [6] to pre-processing, de-noise and segmentation. The Multi-Layer perceptron (MLP) is used to train the extracted features and to classify the image with PKD and without PKD. In [7] a refine method is utilized to do fine segmentation. The coarse segmentation is based on spatial information and K-means fuzzy. Refined segmentation is grounded on Improved Grow Cut (IGC) algorithm. A graph-cuts method is suggested segmentation in US images by mixing texture information and image intensity information [8-10]. Deep CNN and U-Net are demonstrated in recent works, but it is time consuming and computational complexity when the number of layers is increased [11-16]. Although a diversity of approaches have been implemented, many works resolve the kidney segmentation problem as a boundary detection problem Classical FCM frequently loss spatial information resulted in poor performance for image segmentation In this work WOA inspired by the humpback’s social behavior of whales. The contributions are listed as

• •    To develop PKD detection system by implementing a feature based Fuzzy C--means clustering (FFCM) enhanced with WOA for enhancing centroid for segmentation and detection.

• •    To optimize the segmentation process with the whale optimization algorithm to do fitness value for the accurateness in IKD database MRI images.

• •    To compare the experimental results with prevailing methodologies refereed in previous research so as to enable the prominence of the suggested PKD detection system

2.    Materials and Methods

• 2.1    PKD Image Preprocessing

The work is organized as follows. The proposed PKD detection method for diagnosing PKD is illustrated in Section 2. The experimental findings and a comparison with the current approaches are available in Section 3. The conclusion part of the paper is in Section 4.

The articulation of Proposed PKD system using Optimal WOA feature with FFCM segmentation algorithm is detailed below Fig. 1. Initially the probe images are converted into blocks and all the attributes are detached so that FFCM features are optimally joins the group centroids using WOA. The centroid function is considered to show the intensity of MRI of kidney cyst. Here, the tumor/cyst segment from the normal and abnormal types of kidney clustered segment, the suggested PKD system is articulated.

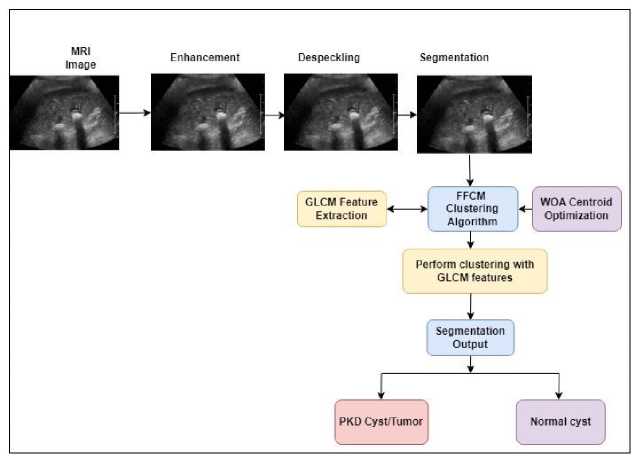
Fig. 1. Articulation of PKD system

Medical Image Preprocessing is a vital part of diagnosis and detection of disease. The main aim is to enhance the quality and to eliminate the removable noise. The image enhancement and de-speckling are the two preliminaries in preprocessing. To enhance the quality of kidney images, a sigmoid filter is used. The input image is considered as H and then sigmoid filter is applied. The mathematical representation is as follows

^Enh   ^(Hmax  Hmin) ^    iT^ri                                  (1)

1+е v +н_т[_п

The enhanced version of an input image is H Enh . The minimum and maximum gray scale image is represented as Н_тах & m_mln. a and y are the parameters to represent the center and width of the image. The preprocessed image is shown in Figure 2.

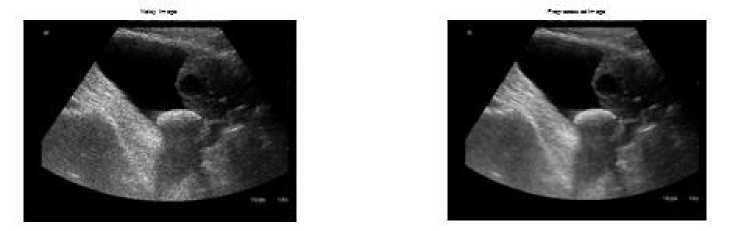
Fig. 2. MRI Noisy Image and preprocessed Image

After preprocessing, bilateral filter is proposed for despeckling. This kind of speckle noise and analyzes its performance.

x⁽t) = Z_s en(t) W ⁽ s,t ⁾ z(s)

Assuming the multiplicative model z(t) = x(t)u(t) with x(t) and z( t) are the true and observed intensity values of pixel t. u( t) is the gamma random variable and the weighted average of predictors z(s) is drawn from a small neighborhood Ω(t). The weight associated with the predictor is given us to prevent over-filtering.

w (s,t) = Cexp{—a\\s — t\\² + A_od_o[o(s),o(t)] — A_sd_s[z(s),z(t)])

The normalizing constant is C and the weights Л_O,A_S depend on spatial distance as well as amplitude distance. The normalized Euclidean distance is computed as

d о (s,t) = -^L ^ _ke p [O i (s + k} — O i ( t + k)]²

M is the number of bands. p is the patch size t is the patch center in spatial offset and S is the search area. The distance is the random variable with homogeneous signal and is denoted as

D [u(s),u(t)] = I о g №==]

^u(s)u(t)]

As we know that u(s)u(t) are the independent Gamma distributed RV’s with unity mean and the shape parameter varies from L=1, L=4 and L=16.

The edges and boundaries are clearly visible after de-speckling. The comparative study is made to show that the proposed bilateral de-speckling filter resulted in removing speckle noise as shown in Figure 4.

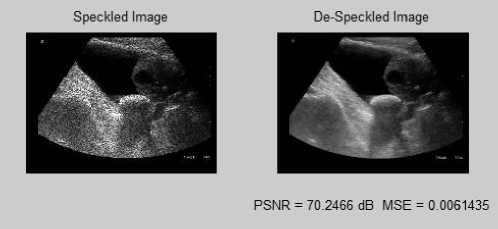
Fig. 3. De-speckled image output

Speckled Image Savitzky-Golay Filetered Image

Original Image

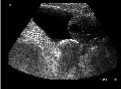
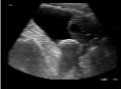
Median Filetered Image

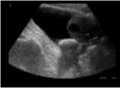
De-Speckled Image

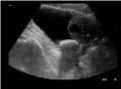
PSNR = 70.2466 dB MSE = 0.0061435

Fig. 4. Comparative study of proposed de-speckling

• 2.2    Feature based FCM (FFCM) clustering for segmentation

Feature based FCM is centered on clustering by curtailing an objective function There are hard clustering and soft clustering algorithms, k-means is a hard clustering algorithm and is searching to initial clustering centers or membership. C-means is a soft algorithm that recovers the deficiencies of k-means at the cost of increasing iterations.

Fig. 5. Attributes of Feature Extraction

Figure 5 is a depiction of feature extraction attributes for consideration. The input image consists of group of attributes which are considered as U = {и ,, и 2,u 3............um } and W = {w1,w2 , w3............wm } are the weight parameters of cluster group centers. The cluster centroid is chosen randomly as n=3.

The fuzzy association function is defined as

^ k = --^                          (6)

The gray-level co-occurrence matrix is denoted as

G ( i,j, о, tp )

l" _XZ" _X G( i, J , о ,

)

G ( i, j, о,cp ) is the frequency component and the adjacent pixels are i and j. o is the offset value and cp is the direction segment.

The fuzzy centroids are calculated as

_ (^jrfuj ) ^w = .z- ^j)^

The distance function n _ dki+dkRt =

D^l represents the amalgamation of pixel and region dissimilarity.

d_kRi   sum ( ) ^∑ i ^∈ RtdkjRi

Ri is the region which is obtained by the mean shift.

In (4) ^R[Rj =‖ mean ( Ri )- mean ( Rj )‖ is the Euclidean distance between the mean values of neighborhood regions. Z is a normalized constant. Instead of using pixels for clustering problem, gray levels are taken into account for decreasing the computational complexity. The objective function of proposed FFCM is

^m =∑    ^∑ k^lYi^k , I ^‖ f^l

-

V_k ^‖2

In (5)  , is the fuzzy membership of gray value l and the weighting exponent m in association with the kth clustering center vk ,f is a gray level image with gray level values 1≤I≤q, Yi is the number of pixels.

^∑    =

The enhanced FCM implements the histogram to reduce the complexity. The objective function От is to minimize and update the membership function

minO_x ( S , W )=∑  ∑ к=1^к ^r2 ( _Uj , W_k )

Where s =[ ^-jk ]    and rfk ( Uj , ^wk )=‖ Uj - ^wk ‖ represent the distance.

The proposed FFCM algorithm is summarized as follows. Initialize randomly the membership partition values, cluster centers, fuzzification degree, weighting factor and error.

• 2.3    Whale optimization algorithm

The whale optimization algorithm is a meta-heuristic algorithm presented to make the universal optimum for fuzzy centroid function until the segmentation quality is met. WOA is inspired by the actions of humpback whales hunting process. It swims in the prey oriented region at a circle which will be reduced slowly with a spiral shaped nature. Here the algorithm is used to explore or exploit basis depends on searching or foraging for prey.

Step 1: Initialization

The population is initialized with $1 ( i =1,2,3… m ) N set cluster centroid, coefficients U and V , Maximum Iteration count x and optimum vector ^⃗⃗⃗ _∗ ^⃗ ()

Step 2: Fitness Function

The task is to optimize the centroid value based upon the accuracy of segmentation function.

f ( Si ) =max( segmentationaccuracy ₎₌

J K                                  J TP+TN+FN+FP

We know that TP-True positive, TN-True negative

FN-False Negative and FP –False Positive

Step 3: Surrounding Prey

As already explained Humpback whales find the finest location and increase the quantity of iteration.

⃗ =| v . ⃗⃗⃗ _∗ ⃗ ( x )- S ( x )|

⃗ ( X +1)= ∗ ⃗ ( X )-

⃗ ⃗ ․ ⃗⃗⃗⃗ if d <0.5

Step 4 Updating Spiral position

The position are updated in spiral form to attack the prey and the mathematically represented as

⃗⃗ • V     4

⃗ ( X +1)= ^⃗ _ehx соѕ(2 Til ) + ⃗⃗⃗ _∗ ⃗ ( X ) if d ≥0.5

Step 5 Searching for prey

-?

⃗⃗⃗⃗⃗⃗⃗⃗⃗ ( X )- S ( X )|

| ^{⃗ ⃗} |>1 – Exploiting FFCM algorithm

| ^{⃗ ⃗} |<1 – Explore and update the finest centroid.

Step 6: Termination

After completion of the maximum iteration, cluster centroid is fixed and the finest collection of segmentation results are the outcome of WOA enabled feature based FCM. Each pixel is assigned to the closest cluster center in the order of the minimum distance, and we then compute the new clusters of cities. The cycle is repeated until it is finished Criteria is satisfied.

• 2.4    Feature Extraction using Gray-Level Co-Occurrence Matrix

The Gray-level Co-occurrence matrix is the technique used here for feature extraction. Image texture analysis is used here to extract distinguished features of a kidney tumor or kidney cyst and the soberness of PKD. The objective of GLCM is to allocate an identified model into groups of images.

Feature based FCM + WOA clustering Algorithm

Initialize	:   Values for Ajk , n , W, S° =[0] e- Termination criterion {0, 1]
Ensure	all center vectors W^ :   all membership degrees ^Jk loop counter b = 1
Repeat	:   update clustering centroid using WOA update membership degrees update objective functions
Until Return Apply	:   ‖ 0^ - ^m ‖< e , b >1 :   Membership degrees ^ki Each data item into the cluster whose ^Jk >  max End if

The size is reduced to speed up the testing and training phase of the system and also the system to ameliorate the quality of the image. The performance is evaluated using the parameter mean square error (MSE) which is adopted as fitness function during the training phase of CAD system and is expressed as

MSE=∑ j ∈ t^∑ P=1 (t ^Jp -уp)

^p is the labeled class and Ур is the obtained output from the CAD system.

3.    Results and Discussion 3.1    Dataset used

The publicly available database for analyzing PKD disease image is used for evaluation and the discussed methodology is experimented as well to improve and assist the diagnosis of the PKD severity.

The considered database consists of 118 images with 512×512 pixels per slice. The region of interest is kidney background and tumor/cyst part with which the segmentation grading scale is fixed as per the latest medical standard. All kidney cyst greater than 1.5 mm is the degree of PKD symptom and is graded for severity. Patients vary in size from microscopic to around 5 cm in diameter, with a thin, transparent wall. These cysts can be linked to major diseases that impede kidney function but don't frequently result in consequences.

US chronic disease indicators: The dataset population offers a consensus-developed cross-cutting collection of 124 indicators that enable states, territories, and major metropolitan areas to consistently define, gather, and report data on chronic diseases.

Table 1. Summary of PKD results

Dataset	PKD % of detection	Degree Scale	Degree of cyst severity
IKD - 50 Normal images	87%	0 %	No visible Tumor/cyst
IKD – 68 abnormal images	90%	1-24 %	Minimal effect
	93%	25-49 %	Mild effect
	86%	50-69 %	Moderate effect
	91%	70-99 %	Severe PKD
	90%	100 %	PKD affected

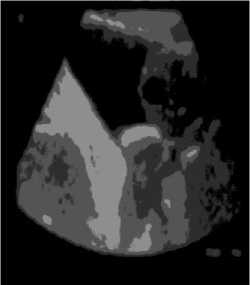
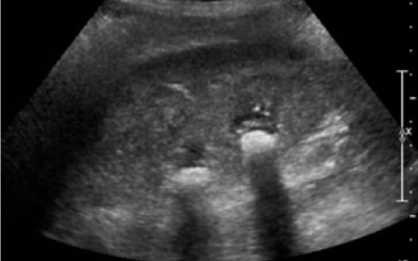
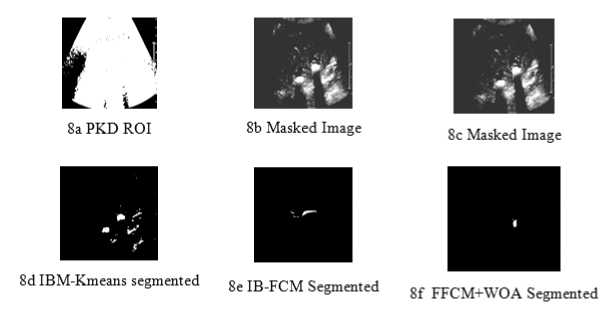
A diagnostic system can frequently arise when evaluating PKD. These patients may exhibit general symptoms like shortness of breath or chest pain. To demonstrate the proposed FFCM, we segment images in real time and compare the results with recent literature. Performance metrics of the FFCM are contrasted with those of the well-known benchmark segmentation algorithms BSDS and MSRC. It is observed that 45 out of 50 photographs are recognized as healthy hearts without occlusion and 54 out of 68 images were diagnosed as having occluded arteries. True positive classification accuracy is 83.07%, and true negative classification accuracy is 90%.

If the patient presents with symptoms of a renal cyst, such as obstruction of the urine or stomach pain, the differential diagnosis is broad. Because the tissues of the kidneys are symmetrical, pain caused by a renal cyst can be traced to almost any organ. It's crucial to keep in mind, too, that most kidney cysts are asymptomatic and are usually found by chance.

Segmentation result

Fig. 6. Proposed FFCM Segmentation Image(without optimization)

Fig. 7.FFCM+WOA segmented Image(with optimization)

Fig. 8. 8a PKD ROI: 8b Masked Image : 8c masked image: 8d IBM-K means segemented :8e IB-FCM Segemented 8f FFCM WOA Segmented

Table 2. Comparison of Performance parameters

S.No	Parameters	MGRF [15]	FFCM+WOA
1	MSE	0.3664	0.025
2	PSNR	52.4911	70.245
3	Loss Percentage	20	13
4	Accuracy	94	97

The performance of the proposed and existing classification procedures is compared in Table 2 using Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR) metrics. These two error measures are what are utilized to compare image quality. The total squared error between the input and output images is known as the MSE. For low MSE levels, the error is also reduced. The PSNR shows the peak signal-to-noise ratio (in decibels (dB) between two images. This ratio is used to assess the image quality of the input and output. High PSNR levels result in greater image quality.

Table 3. Performance metrics

Method	Precision	Recall	Accuracy	Dice
FCM	0.95	0.875	0.85	0.762
EFCM+WOA	0.95	0.925	0.97	0.764

Because of our model's excellent accuracy (97.%), there is very little chance that it will be misdiagnosed, which is crucial for practical use. In addition, our model has a high recall (92.52%), which indicates that there is very little chance of a missed diagnosis.

A small portion of the pixels in the ROIs of a medical segmentation picture are often marked as background, with the remainder pixels being part of the image. Since the accuracy score takes into account actual negative results, it will always produce an erroneous high score.

By comparison, the most often used metrics for semantic segmentation are IoU and dice coefficient because they penalise false positives, a typical feature in highly class unbalanced datasets such as MIS. Nevertheless, depending on the task's particular use cases, one may prefer to employ dice coefficient over IoU or vice versa.

Table 4 Classification Performance of the proposed WOA+EFCM with existing classifiers

Contributers	Data	Method	Accuracy (%)	Sensitivity (%)	Specificity (%)
[10]	US	SOM-SVM	87.51	86.12	88.54
[11]	US	LFO-ASVM	93.62	90	96.24
[13]	WDBC	MBA-RF	96.71	91.32	93.23
[17]	CT	BAS-BPNN	96.31	96.32	95.62
Proposed method	MRI	WOA + FFCM	97	96.43	94.9

The medical image datasets are collected for using various scanners and imaging methods, an effective technique using transfer learning was applied to fine-tune the categorization task and increase accuracy. It was observed that the classification accuracy of the available approaches was 87.51% (SOM-SVM), 93.62% (LFOA-SVM), 96.71% (MBA -RF), and 96.31% (BAS-BPNN) [10, 11,13, 17].

4.    Conclusion

It is essential to diagnose kidney disease using MRI scanning techniques. Doctors can make more precise decisions with the aid of the proposed PKD model. This research suggested a CAD model that combines a whale optimization with the feature based FCM method to diagnose kidney PKD disease. In this system, the speckle noise was reduced with bilateral filter, and the contrast of the images was improved with a sigmoid filter. The dimensions of the resulting features were reduced by GLCM. After that, FFCM+WOA was employed to optimize the segmentation process. For training and centroid optimisation, traditional FCM needs more time. This suggested method utilized the knowledge of GLCM and fix finest FFCM to modify the weighting factors, thereby speeding up training and computation.