Z-коэффициент как параметр автоматической классификации текстов

Классификация текстовых документов - направление информационных технологий, которое имеет непосредственное значение для адекватного функционирования информационно-поисковых систем, электронных библиотек, систем анализа мнений пользователей, программ фильтрации спама, систем распознавания плагиата и экстремистского контента, авторской атрибуции текстов [4]. Автоматическая классификация выполняется программой-классификатором, выдающей пользователю имя класса, с которым соотносится входной текст. Под классом обычно понимается жанр; тематическая рубрика или категория; кластер - группа документов, объединённых по некоторому признаку. С целью их выявления проводится анализ распределения лингвистических единиц текста (терминов), соответственно, программы-классификаторы относятся к лингвистическому программному обеспечению. Поскольку предполагается, что имя класса не выражено в явном виде, а его распознавание требует применения эвристических методов, классификаторы относятся интеллектуальным информационным системам. Классификаторы относятся к программному обеспечению, предназначенному для поддержки принятия решений, а их пользователями являются менеджеры, администраторы, руководители разных уровней, в полномочия которых входит принятие управленческих решений.

Широкое распространение классификационных технологий делает актуальным разработку новых и модификацию существующих методов классификации с целью повышения её эффективности. Цель настоящей работы - оценить эффективность применения Z-коэффициента в качестве параметра автоматической классификации текстовых документов на примере решения задачи авторской атрибуции текстов.

Программы-классификаторы включают два модуля: модуль предварительной обработки анализируемого текста и модуль основной обработки. Модуль предварительной обработки выполняет распознавание терминов, в качестве которых могут выступать стеммы, леммы, слова, словосочетания (n-гра-мы), предложения. Модуль основной обработки выполняет: 1) взвешивание терминов; 2) вычисление индекса анализируемого текста; 3) сопоставление индекса текста с индексом некоторого эталонного текста или корпуса текстов и определение класса анализируемого документа. По результатам взвешивания каждому термину приписывается числовой коэффициент, отражающий его дискриминатив-ную силу – способность идентифицировать данный класс текстов. Высокие числовые коэффициенты указывают на большую дискриминативную силу. Числовые коэффициенты, приписанные терминам, являются параметрами классификации. На основе параметров вычисляется общий индекс документа, который сопоставляется с индексом эталонного текста или корпуса, включающего тексты, наиболее типичные для данного класса. По результатам сопоставления вычисляется либо степень смысловой близости между анализируемым и эталонным текстами, либо расстояние между ними. В первом случае применяется словарный подход, во втором - дистантный. В соответствии с дистантным подходом меньшее расстояние указывает на большую близость документов и большую вероятность того, что они относятся к одному классу. Если применяется словарный подход, то, напротив, больший числовой коэффициент указывает на большую близость документов.

В рамках словарного подхода начисляются коэффициенты за каждое вхождение в анализируемый текст терминов из заранее составленного словаря, а индекс документа определяется по сумме коэффициентов терминов. В рамках дистантного подхода анализируются различные виды отклонений распределения единиц текста от некоторого распределения, которое считается эталонным для данного класса. Меньшее отклонение указывает на большую близость текста к этому классу. Широко применяется среднеквадратичное отклонение, которое вычисляется как квадратный корень из дисперсии случайной величины. В современных математических и табличных процессорах, языках программирования дисперсия, а иногда среднеквадратичное отклонение (σ), высчитывается автоматически. Ранее [1] мы показали возможность использования среднеквадратичного отклонения для вычисления индекса документа на основе отклонений распределения стоп-слов от коэффициента Ципфа. Ещё одна метрика, которую можно использовать в рамках дистантного подхода – Z-коэффициент [3, 6], позволяющая высчитывать отклонения отдельных терминов, в отличие от среднеквадратичного отклонения, применяющегося ко всему числовому ряду. Z-коэффициент вычисляется по формуле:

Zq(t ) = iZ_^22

где f - частотность термина t., ц - среднеарифметическая величина частотностей терминов данно- го текста, σ – среднеквадратичное отклонение.

Вычисление Z-коэффициента с целью классификации текстов предусматривает выполнение следующих процедур. 1) Находятся частотности терминов данного текста и составляется ранжированный список. Нами в качестве терминов будут использованы стоп-слова из расширенного списка Фокса, включающего 426 терминов [7], а их частотности будут находиться с помощью разработанного нами приложения Y-sets [8]. 2) Для числового ряда с частотностями терминов находятся среднеарифметическая величина и среднее квадратичное отклонение. 3) По формуле (1) для каждого термина вычисляется Z-коэффициент. Коэффициенты терминов представляют собой классификационные параме- тры. 4) На основе параметров вычисляется индекс всего текста. Он может быть вычислен как сумма коэффициентов отдельных терминов. Заметим, что вычисления по формуле (1) могут давать отрицательные коэффициенты. В этом случае классификационный индекс текста может вычисляться на основе только положительных значений отклонений терминов. Поскольку термины с положительными значениями Z-коэффициента занимают позиции вверху ранжированного списка, переход к отрицательным значениям может служить пороговым уровнем, отделяющим термины с наибольшей дискримина-тивной силой. 5) Полученный индекс документа сопоставляется с индексом эталонного текста – текста наиболее типичного для данного класса документов. Расстояния между текстами вычисляются как разница по модулю между индексами. Меньшая разница будет указывать на большую близость текстов и вероятность того, что они относятся к одному классу. В качестве эталонного текста нами был взят роман английского писателя XIX в. Ч. Диккенса Oliver Twist (файл Tw), который считается типичной и одной из наиболее известных работ автора, а в качестве входных текстов - книга того же автора Nicholas Nickleby (файл Nb) и произведение английского автора начала XX в. Дж. Голсуорси The Man of Property (файл Mn). Книги были загружены с портала проекта Гутенберг [2], на котором размещаются отредактированные и вычитанные произведения с истекшим сроком авторского права. Из этих текстов нами были удалены сведения о самом проекте. Выбор художественных текстов объясняется большим разнообразием лексического состава; также произведения авторов XIX – начала XX века характеризуются большим объёмом, что позволяет получать достоверные сведения об отклонениях распределения анализируемых терминов.

Таким образом, задача тестирования состояла в том чтобы найти расстояния между текстами одного автора и текстами разных авторов: Dis( Nb, Tw ), Dis( Mn, Tw ). Если Dis( Nb, Tw )Mn, Tw), то это будет подтверждением возможности использования метрики “Z-коэффициент” с целью классификации текстов. Если же Dis(Nb, Tw)>Dis(Mn, Tw), то это будет свидетельствовать о неэффективности данной метрики. В табл. 1 приводятся статистические данные анализируемых текстов и их индексы, полученные в результате суммирования Z-коэффициентов отдельных терминов с положительными значениями этого коэффициента.

Таблица 1

Статистические данные и индексы текстов

Проведенный тест дал отрицательный результат: Dis( Nb, Tw )=| 92.816-84.745|=8.071, Dis( Mn, Tw )=|86.635-84.745|=1.89. Расстояние между текстами разных авторов оказалось на 76.6% меньше, чем расстояние между текстами одного автора. Можно предположить, что на результат повлияла значительная разница в размерах текстов: в файле Nb в 2.05 раза больше токенов, чем в файле Tw , и в 2.9 раза больше, чем в файле Mn . В этой связи было решено выровнять тексты по размеру с помощью выравнивания по нижнему пределу и повторить экспериментальный тест, применив ту же методику. Выравнивание по нижнему пределу предусматривает удаление части текстов, так чтобы у них осталось такое же количество токенов, как в самом маленьком по размеру тексте. В нашем случае таким текстом является файл Mn , содержащий 113149 токенов. Соответственно, с конца двух других файлов были удалены части текстов, с тем, что в них осталось такое же количество токенов. В таб. 2 (на с. 232) приводятся результаты второго теста.

Таблица 2

Статистические данные и индексы выравненных текстов

Второй тест также дал отрицательный результат: Dis( Nb, Tw )=|87.37-82.16|=5.21, Dis( Mn, Tw )=|86.635-82.16|=4.476. Расстояние между текстами разных авторов оказалось на 14.093% меньше, чем расстояние между текстами одного автора. В этой связи было решено провести третий экспериментальный тест, использовав в качестве параметра отклонение от распределения Ципфа, которое применяется в разработанном нами ранее Y -методе автоматической классификации текстов [1]. В соответствии с этим методом для каждого термина вычисляется коэффициент Ципфа по формуле:

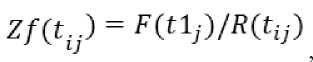
где '■ ' ' - частотность первого по рангу термина t . в некотором j -м тексте, а R - номер ранга слова. Далее для каждого термина вычисляется отклонение от коэффициента Ципфа как разница по модулю между частотностью термина и его коэффициентом. Индекс текста вычисляется как среднее квадратичное числового ряда, содержащего отклонения. В задачу настоящей работы входит тестирование Z -коэффициента, поэтому индексы текстов будут вычисляться на основе числового ряда с положительными Z -коэффициентами, которые находятся на основе отклонений от распределения Ципфа. Таким образом, последовательно создаётся пять числовых рядов: ряд R с рангами слов; ряд F , содержащий реальные частотности слов; ряд Zf с коэффициентами Ципфа; ряд DevZf , включающий разницы по модулю между двумя показателями, ряд Zq , содержащий Z -коэффициенты терминов. В таб. 3 результаты вычислений для первых трёх терминов и индексы текстов. Тест проводился на выравненных текстах, данные которых приводятся в таб. 2.

Таблица 3

Результаты вычислений (выборка) и индексы текстов

Данный тест дал положительный результат: Dis( Nb, Tw )=|112.294-115.287|=2.992, Dis( Mn, Tw )=|100.361-115.287|=14.925. Расстояние между текстами одного автора оказалось на 79.952% меньше, чем расстояние между текстами разных авторов.

В заключение отметим, что Z -коэффициент обычно используется для нормализации других параметров [5]. Нами впервые было проведено тестирование возможности его использования в качестве отдельного параметра при решении задачи авторской атрибуции в рамках дистантного подхода к классификации текстовых документов. Было проведено три теста: на полных текстах, на выравненных текстах, на выравненных текстах в сочетании с отклонениями от распределения Ципфа. Экспериментальное тестирование показало, что использование указанного коэффициента в качестве отдельного параметра даёт отрицательный результат как на полных, так и на выравненных текстах. Положительный результат был достигнут в результате последнего теста, когда Z -коэффициент вычислялся на основе отклонений от распределения Ципфа. Таким образом, была подтверждена высокая эффективность использования этого вида отклонения для решения задач автоматической классификации текстовых документов. Использование отклонений от распределения Ципфа лежит в основе разработанного нами Y-метода автоматической классификации, который на художественных текстах показывает примерно такую же (более 80%) эффективность. В принципе, методику, предложенную в последнем тесте, можно рассматривать как вариант Y-метода. Следует, однако, отметить, что применение этого варианта предусматривает выполнение более сложных вычислений и создание дополнительного числового ряда с Z -коэффициентами. Очевидно, что необходимо провести дальнейшее тестирование этого варианта на текстах, относящихся к другим жанрово-стилистическим группам, например, научных и газетных.