Задача интерполяция функция с помощью кубическое сплайна

Слово "spline" в переводе с английского означает "упругая рейка". Такую рейку используют в качестве гибкого лекала при вычерчивании плоских кривых по опорным точкам (рис.1). Форма осевой линии рейки на участке между двумя соседними опорами описывается функцией[1].

Широкое распространение для интерполяции получило использование кубических сплайн-функций - специальным образом построенных многочленов третьей степени. Они представляют собой некоторую математическую модель гибкого тонкого стержня из упругого материала. Если закрепить его в двух соседних узлах интерполяции с заданными углами наклонов а и в (рис. 1), то между точками закрепления этот стержень (механический сплайн) примет некоторую форму, минимизирующую его потенциальную энергию.[1]

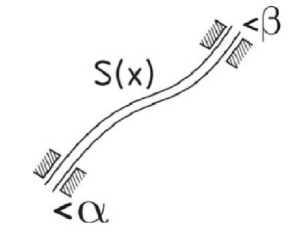
Рис. 1. Сплайн-функция

Для того что бы решить это задачу давайте с начала решим частная задачу рисуем что на отрезке от 0 до 1 у нас задним функция многочлен третей степени S(x) известная а коэффициенты пока неизвестная. Мы хотим определит по следующем данным по значения функция в точки 0 по производным функция в точки 0 и по значения функция в точки 1 по производным функция в точки 1. То есть известна . если функция S(x)

определяется таким образом то производна функция записываются естества так[3]

Четыре уравнения и удобно была записать матричный вид и потом решить с помощью алгоритм нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы). Для неособенной квадратной матрицы P обратной является матрица[2].

Где - определитель матрицы P , а - матрица, союзная с матрицей P . Союзной с квадратной матрицей P называется матрица того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы , транспонированной относительно матрицы P . Таким образом, если[2], и

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

• 1.    Найти определитель данной матрицы P . Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

• 2.    Найти матрицу, транспонированную относительно P .

• 3.    Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

• 4.    Применить формулу (2): умножить число, обратное определителю матрицы P , на союзную матрицу, найденную на шаге 4.

• 5.    Проверить полученный на шаге 4 результат, умножив данную матрицу P на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно.[2]

Здесь, для чего все это нам нужно вычислит второй производный функция S(x) где k=1, 2, ..., n-1 Таким образом мы самом дело получили систему лиленых уравнения отнисително zk . Мы используем граничные условие так (можно использовать другая граничные условие) ,Это система имеет такое матрица, Система уравнения выгладить так, Данная система уравнений однозначно определяется расширенной матрицей системы.

Решим систему уравнений с помощью C#.

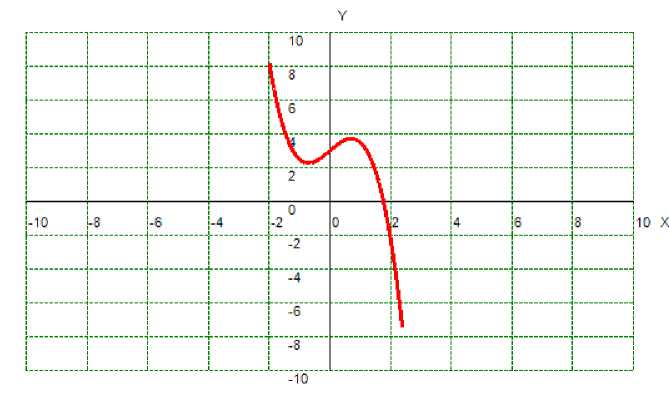
Сплайн-функция . –М.: Машиностроение, 2014. – 1 с.

Тонис. Лекция 7.4. Кубические сплайны – 1, 2

"Экономика и социум" №12(55) 2018