Задача минимизации доз облучения при техническом обслуживании АЭС

Автор: Ляхов Олег Алексеевич

Журнал: Проблемы информатики @problem-info

Статья в выпуске: 1 (30), 2016 года.

Бесплатный доступ

Показано, что условие однократного обхода вершин в математической формализации задачи оптимизации траектории перемещения работников в радиационно опасных зонах приводит к потере эффективных решений. Ослабленное условие - „посетить каждый объект не менее чем по одному разу" способствует уменьшению облучения персонала АЭС. Определены условия, при которых оптимальные решения задач в стандартной формулировке и с ослабленными условиями совпадают и различаются. Рассмотрен способ решения "ослабленной" задачи. Приведены численные примеры.

Техническое обслуживание аэс, математическая модель, выбор маршрута, минимизация доз облучения

Короткий адрес: https://sciup.org/14320296

IDR: 14320296

Текст научной статьи Задача минимизации доз облучения при техническом обслуживании АЭС

Введение. Комплекс мер, направленных на снижение облучения персонала АЭС, включает совершенствование управления радиационно опасными работами. В [1, 2] выделены этапы цикла управления ремонтными работами АЭС, включающего планирование, подготовку, выполнение и оценку результатов работ; регламентированы функции этапов, рассмотрены методы оценки доз облучения. В [3] предложена математическая модель, которая может быть использована в управлении радиационно опасными работами на этапе составления планов. Модель предназначена для построения маршрутов передвижения ремонтного персонала по зараженным участкам, снижа ющего суммарное облучение. Исходная формулировка задачи заключается в следующем:

— техническое обслуживание и ремонт АЭС в зоне с высоким уровнем радиации сопряжены с облучением ремонтного персонала, которое складывается из доз, получаемых при выполнении работ, включая подготовительно-заключительные операции, и доз, получаемых при перемещении от одного объекта к другому;
— требуется определить маршрут передвижения ремонтного персонала по зараженным участкам, минимизирующий суммарное „транзитное¹¹ облучение.

В [3] предложено использовать задачу коммивояжера для решения этой проблемы. Там же приведена незамкнутая задача коммивояжера с требованием обхода всех вершин без возврата в исходный пункт.

Задача коммивояжера формулируется следующим образом: требуется найти наиболее короткий маршрут путешественника (бродячего торговца, транспортного средства и т. д.), которому нужно посетить каждый город из заранее заданного списка по одному разу и вернуться в исходный пункт (незамкнутая задача не требует возвращения в начальную точку). В теории графов задача сводится к поиску гамильтонова контура минимальной длины. Она также может быть поставлена как комбинаторная или как задача целочисленного программирования (см., например, [4], Т. 2, С. 252-254).

Задача коммивояжера широко используется в различных сферах человеческой деятельности от календарного планирования до проектирования сложных технических систем. Наиболее известные практические проблемы, сводящиеся к задаче коммивояжера, — задача о переналадках [5, С. 231], [6, С. 93], задача о коммуникациях [7, С. 166], задача составления расписаний транспортных средств и многие другие, — не всегда полностью соответствуют их математической формализации. Условие однократного посещения каждого пункта (условие „однократности“) является излишним по отношению к большей части исходных ситуаций. Так, в [4, Т. 1, С. 162] требуется определить маршрут минимальной длины школьного автобуса, подвозящего на занятия учеников из различных районов города. В [3] приведена следующая постановка: требуется выполнить работы на всех заранее заданных объектах (местах выполнения работ); известны дозы облучения, получаемые при перемещении между технологическими операциями; требуется так составить маршрут передвижения ремонтных бригад, чтобы суммарная доза облучения, полученная при перемещении между объектами, была минимальной. При этом каждый объект посещается один раз. Однако, если выгоднее посетить один из пунктов дважды, то этому ничего не препятствует, кроме условия однократности, которому трудно найти объяснение, исходя из словесных описаний проблемы доставки учеников на занятия или минимизации доз облучения при ремонте АЭС.

Большое число публикаций посвящено методам решения задачи коммивояжера, тогда как оценка степени пригодности математической модели для тех или иных реальных ситуаций (верификация) нечасто привлекает внимание исследователей.

В данной статье рассмотрены вопросы адекватности модели, используемой для решения задачи коммивояжера, реальной практической проблеме минимизации облучения ремонтного персонала АЭС. Описаны случаи потери эффективных решений в связи с требованием однократного посещения зараженных участков. Предложена модель с возможностью повторного посещения пунктов, которая позволяет сократить дозу облучения ремонтных бригад. Приведены численные примеры, подтверждающие снижение облучения персонала в сравнении с известной задачей коммивояжера.

Потеря эффективных маршрутов перемещения работников в радиационно опасных зонах в связи с условием „однократности" в задаче коммивояжера. Несоответствие модели задачи коммивояжера с условием „однократности¹¹ исходной постановке может быть иллюстрировано составлением маршрута ремонтного персонала по зараженным участкам АЭС на примере, приведенном на рис. 1, где каждой дуге сопоставлено расстояние между пунктами (обозначенными кружками), которые она соединяет. В данном случае это дозы облучения, получаемые при перемещении от одного объекта к другому.

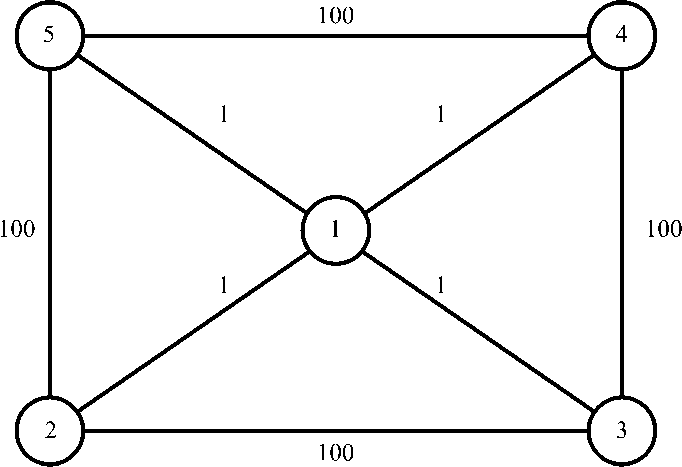
Рис. 1. Графическая модель перемещения ремонтной бригады

Минимальное облучение в исходной задаче коммивояжера составляет 302 (маршрут 1—>2—>3—>4—>5—>1 ), а с повторным посещением вершин — 8 (маршрут 1—>2—^1—>3—^1—>4—^1—>5—^1).

Вследствие требования посещения каждого объекта по одному разу ремонтный персонал вынужден передвигаться по дугам (2, 3), (3, 4), (4, 5), тогда как дуги (1, 3), (1, 4), (1, 5) не вошли в оптимальный план из-за требования однократного включения в маршрут вершины 1.

Пусть в условиях примера невозможно непосредственное передвижение по дугам (2, 3), (3, 4), (4, 5), (5, 2) в прямом и обратном направлениях. Тогда не существует ни одного неограниченного по дозе облучения решения задачи коммивояжера с условием „однократности", а оптимальный маршрут „ослабленной" задачи остается прежним.

Таким образом, излишнее относительно постановки задачи условие приводит к потере эффективных, а иногда и допустимых решений.

Решение „ослабленной⁴⁴ задачи коммивояжера. Задачу коммивояжера, в которой разрешено только одно посещение вершины (в дальнейшем — задачу 1), сопоставим с задачей коммивояжера с возможностью неоднократного посещения вершин (задачей 2). Обозначим через х^ число проходов по дуге ^г,з\г,з = 1,п, где ?г — количество вершин (объектов ремонта, городов и т. д.).

В математической модели задачи 1 условия „однократности" формализуются следующим образом (по одному входу и выходу для каждой вершины):

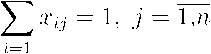
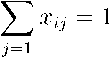
г = 1,п, где Ху Е [0,1], целые.

Для задачи 2 эти соотношения заменяются на балансовые уравнения (число входов в вершину равно числу выходов): 52 ^xij = 52 ^ХЛ 3 ⁼ Ф^и, ^гД^е ^xij ^ 0, целые.

2=1 г=1

Пусть А = {«у} — матрица, в которой о-у ^ 0 - исходное расстояние между вершинами г и j. Расстояние интерпретируется в зависимости от конкретной формулировки задачи. Это может быть продолжительность, вес, доза облучения и т. д. В обеих задачах целевая функция — минимизация затрат обхода всех вершин и возвращения в исходную точку — п п записывается одинаково: И аижи "^ min. Л' = {а^} — матрица, в которой аб > О минимальное расстояние из г в ф г, j = 1,п. Задача 2 может быть сведена к задаче 1 заменой исходной матрицы А на Л' [9, С. 652; 10, С. 19].

Для обеих задач справедливы следующие два утверждения.

1. Если для всех дуг (г,Д, гД = 1,щ выполнено неравенство треугольника а^ < min Д^ + ск^-), то оптимальные решения задач 1 и 2 совпадают.
2. Каждому оптимальному решению задачи 1 с матрицей К соответствует оптимальное решение задачи 2 с матрицей А.

Действительно, несовпадение решений задач 1 и 2 означает, что в оптимальном пути задачи 2 обязательно найдется вершина г, посещенная более одного раза. Из этого следует нарушение условия неравенства треугольника на дуге между непосредственно предшествующей и непосредственно следующей за вершинами. Таким образом, задачи 1 и 2 для матриц с выполненным неравенством треугольника эквивалентны.

Решения задач 1 и 2 с матрицей А' совпадают. При этом любое решение задачи 2 с матрицей А' является допустимым для задачи 2 с матрицей А. Из а^ ^ «б A j = 1,/г, следует, что оптимальное решение задачи 2 с матрицей А „не лучше“ решения задачи 2 с матрицей А', для которой задачи 1 и 2 эквивалентны, что доказывает второе утверждение.

Таким образом, решение „ослабленной“ задачи коммивояжера сводится к построению матрицы А', решению задачи 1 с матрицей Л', восстановлению маршрута по дугам оптимального пути ДД, таким, что ащ > аб.

Пример: решение задачи 2 (см. рис. 1).

А =

" 0 1 1 1 1 "

1 0 100 100 100

1 100 0 100 100

1 100 100 0 100

1 100 100 100 0

; ^ =

"01111"

1 0 2 2 2

1 2 0 2 2

1 2 2 0 2

1 2 2 2 0

Оптимальный путь в задаче 1 с матрицей А* : 1 щ 2 > 3 щ 4 —>5—>1. Заменим дуги 2 —> 3, 3 Д 4, 4 —> 5 на пути минимальной длины, соединяющие начальные и конечные вершины этих дуг: 2 —> 1 —> 3, 3 Д 1 д 4. 4 -д 1 -д 5. Получим оптимальный путь в задаче 2 с матрицей А.

Численные примеры минимизации облучения при ремонте АЭС. В [2, 3] рассмотрены замкнутая задача коммивояжера (вход и выход через один начальный пункт) и незамкнутая, в которой заданы вход и выход и не требуется возврат в исходную точку. Там же для оценки эффективности оптимизации пути перемещения персонала в радиационно опасных зонах были приведены результаты расчетов реальных вариантов. Исходные данные этих примеров, заимствованные из [3, С. 46], приведены в матрице доз облучения при движении работника между ремонтными объектами (в единицах измерения эффективных доз облучения персонала — микрозивертах (мкЗв), ос — недопустимая доза облучения при передвижении между соответствующими объектами или отсутствие прямого пути между ними):

	" 0	8,2	ОО	ОО	ОО	сю	оо	оо	ОС	23,0	5,6	7,5 "
	8,2	0	11,0	'ОО	ОО	оо	оо	ОС	22,0	13,2	9,8	11,0
	ОО	11,0	0	23,0	ОО	оо	17,5	ОС	17,5	22,0	11,5	31,0
	ОО	ОО	23,0	0	7,8	оо	'ОС	21,5	11,0	13,2	24,0	ОС
	ОО	ОО	ОО	7,8	0	11,0	19,0	7,8	16,5	19,8	оо	ОС
А =	ОО	ОО	ОО	ос	11,0	0	19,0	20,0	27,5	оо	00	оо
	ОО	ОО	17,5	оо	19,0	19,0	0	21,0	ос	оо	00	оо
	ОО	ос>	ОО	21,5	7,8	20,0	21,0	0	15,0	оо	ОС	оо
	ОО	22,0	17,5	11,0	16,5	27,5	'ОС'	15,0	0	13,0	оо	оо
	23,0	13,2	22,0	13,2	19,8	оо	'ОС	ОС	13,0	0	10,0	оо
	5,6	9,8	11,5	24,0	оо	оо	оо	ОС	оо	10,0	0	22,0
	7,5	11,0	31,0	ОО	ОО	оо	оо	оо	ос	оо	22,0	0 _

Для данной матрицы А построим маршруты минимальной длины для замкнутой и незамкнутой задачи с использованием „ослабленной¹¹ модели. Рассчитаем А'.

	" 0	8,2	17,1	28,8	35,4	46,4	34,6	43,2	28,6	15,6	5,6	7,5 "
	8,2	0	11,0	26,4	33,0	44,0	28,5	37,0	22,0	13,2	9,8	15,7
	17,1	11,0	0	23,0	30,8	36,5	17,5	32,5	17,5	21,5	11,5	24,6
	28,8	26,4	23,0	0	7,8	18,8	26,8	15,6	11,0	13,2	23,2	36,3
	35,4	33,0	30,8	7,8	0	11,0	19,0	7,8	16,5	19,8	29,8	42,9
А! =	46,4	44,0	36,5	18,8	11,0	0	19,0	18,8	27,5	30,8	40,8	53,9
	34,6	28,5	17,5	26,8	19,0	19,0	0	21,0	35,0	38,8	29,0	42,1
	43,2	37,0	32,5	15,6	7,8	18,8	21,0	0	15,0	27,6	37,6	50,7
	28,6	22,0	17,5	11,0	16,5	27,5	35,0	15,0	0	13,0	23,0	36,1
	15,6	13,2	21,5	13,2	19,8	30,8	38,8	27,6	13,0	0	10,0	23,1
	5,6	9,8	11,5	23,2	29,8	40,8	29,0	37,6	23,0	10,0	0	13,1
	7,5	15,7	24,6	36,3	42,9	53,9	42,1	50,7	36,1	23,1	13,1	0
Оптимальные пути незамкнутой					задачи с		входом через вершину 5					и выходом через

11 приведены на рис. 2. Для условий однократности значение целевой функции в точке оптимума 140,6 мкЗв, для ослабленной задачи — 139,4 мкЗв. В остальных примерах из [3] (их перечень совпадает с приведенным в таблице) решения ослабленной и стандартной задачи совпали.

Таким образом, за счет повторного посещения вершины 5 удалось сократить дозу облучения ремонтного персонала в сравнении с маршрутом стандартной задачи.

В условиях предыдущего примера изменим исходную матрицу А (6 элементов в последних строке и столбце заменены на „М“, что в новой матрице обозначает то же самое, что и знак сю, т. е. невозможность передвижения по соответствующей дуге):

	■ 0	8,2	оо	оо	оо	ОО	ОС	оо	ОС	23,0	5,6	7.5
	8,2	0	11,0	ос-	оо	ОС	ос-	оо	22,0	13,2	9,8	М
	сю	11,0	0	23,0	оо	оо	17,5	оо	17,5	22,0	11,5	м
	сю	ос	23,0	0	7,8	ОС	оо	21,5	11,0	13,2	24,0	ос
	сю	ос	оо	7,8	0	11,0	19,0	7,8	16,5	19,8	оо	ос
А =	оо	ОС	00	оо	11,0	0	19,0	20,0	27,5	оо	оо	оо
	оо	ОС	17,5	ос	19,0	19,0	0	21,0	ос	'ЭС	оо	оо
	оо	ОС	оо	21.5	7,8	20,0	21,0	0	15,0	ОС	оо	оо
	оо	22,0	17,5	11,0	16,5	27,5	ос	15,0	0	13,0	оо	оо
	23,0	13,2	22,0	13,2	19,8	оо	оо	оо	13,0	0	10,0	ОС
	5,6	9,8	11,5	24,0	оо	оо	-ЭС	оо	оо	10,0	0	м
	7,5	М	М	оо	оо	оо	-ЭС	оо	оо	ос	М	0

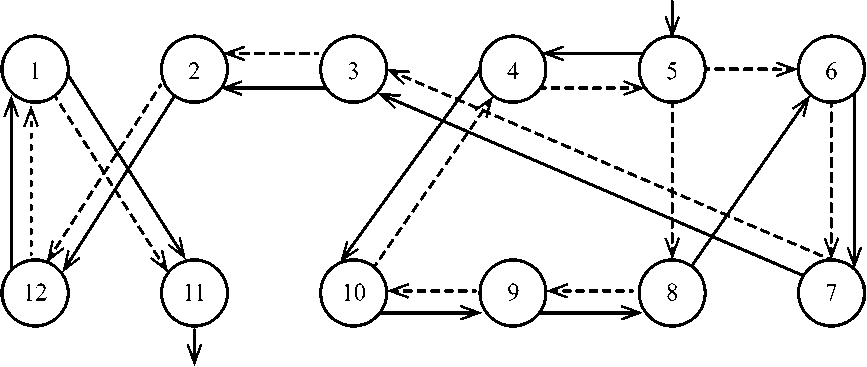
Рис. 2. Оптимальные маршруты (пунктирными стрелками обозначен путь задачи с возможностью повторного посещения вершин)

Результаты решения ослабленной задачи приведены в таблице.

Результаты решения ослабленной задачи

Таблица

	Значение целевой функции (в мкЗв)	Оптимальный путь
Замкнутая задача	144,3	1-2-3-7-6-5-8-9-4-10-11-1-12-1
Незамкнутая задача, вход — 1, выход — 5	143,9	1-12-1-11-10-2-3-7-6-5-8-9-4-5
Незамкнутая задача, вход — 1, выход —11	138,7	1-12-2-3-7-6-5-8-9-4-10-11
Незамкнутая задача, вход — 5, выход — 6	133,3	5-8-9-4-10-11-1-12-1-2-3-7-6
Незамкнутая задача, вход — 5, выход —11	144,1	5-8-9-10-4-5-6-7-3-2-1-12-1-11

Для данного примера нет ни одного допустимого по дозе облучения ремонтного персонала решения задачи с условием „ однократности“.

Заключение. Условие однократного посещения вершин в математической модели задачи коммивояжера не является необходимым для большого числа известных практических ситуаций. Его замена на ослабленное — „посетить каждый пункт не менее чем по одному разу" — способствует улучшению „оптимальных" решений проблем, исходя из их исходных постановок.

На реальных примерах показано, что при построении безопасных маршрутов передвижения ремонтного персонала по зараженным участкам АЭС „ослабленная" модель позволяет уменьшить дозы облучения ремонтных бригад в сравнении с решениями, полученными по модели с однократным посещением объектов.

Приведены примеры, в которых при отсутствии допустимых по дозе облучения маршрутов задачи коммивояжера с условием однократности „ ослабленная“ модель позволяет найти оптимальные решения.

Решение „ослабленной11 задачи сводится к последовательному выполнению следующих действий:

— преобразование матрицы А в А' ;
— решение задачи коммивояжера с однократным посещением вершин одним из известных методов с исходной матрицей расстояний А' ;
— восстановление оптимального решения „ослабленной¹¹ задачи.

Список литературы Задача минимизации доз облучения при техническом обслуживании АЭС

ТАШЛЫКОВ О. Л., СЕСЕКИН А.Н., ГОНЧАР А. А., ЩЕКЛЕИН С.Е. Об алгоритмизации задачи оценки дозовых нагрузок при планировании ремонтного обслуживания АЭС/Сборник трудов седьмой научно-практической конференции, посвященной 40-летию работы Белоярской АЭС. Заречный, 2004. Т. 3. С. 161-166.
ТАШЛЫКОВ О. Л., ЩЕКЛЕИН С.Е., МАРКЕЛОВ Н.И. Математическое моделирование дозовых полей при планировании облучения ремонтного персонала//Ядерная энергетика. 2004. № 1. С. 39-44.
СЕСЕКИН А. Н., ТАШЛЫКОВ О. Л., ЩЕКЛЕИН С. Е. и др. Использование метода динамического программирования для оптимизации траектории перемещения работников в радиационно опасных зонах с целью минимизации облучения//Ядерная энергетика. 2006. № 2. С. 41-48.
ВАГНЕР Г. Основы исследования операций. М.: Мир, 1973.
СМОЛЯР Л. И. Модели оперативного управления в дискретном производстве. М.: Наука, 1978.
ШКУРВА В. В. Задача трех станков. М.: Наука, 1976.
Плотников В. Н., ЗВЕРЕВ В. Ю. Оптимизация оперативно-организационного управления в дискретном производстве. М.: Машиностроение, 1980.
Исследование операций/Под. ред. Моудера Д., Элмаграби С. М.: Мир, 1981.
HARDGRAVE WILLIAM W., NEMHAUSER GEORGE L. On the Relation Between the Traveling Salesman and the Longest Path Problems//Operations Research. 1962. V. 10. N 5. P. 647-657.
МЕЛАМЕД И. И., СЕРГЕЕВ С. И., СИГАЛ И. X. Задача коммивояжера. Вопросы теории//Автоматика и телемеханика. 1989. № 9. С. 3-33.

Еще

Статья научная