Задача моделирования аппаратурных спектров гамма-излучения от облака радиоактивного выброса на АЭС в рамках развития концепции гибридного мониторинга

В ИБРАЭ РАН на протяжении длительного времени ведутся исследования по развитию подходов и методов для совершенствования концепции гибридного мониторинга [1]. Гибридный мониторинг предполагает использование расчётного моделирования и данных измерений для проведения прогноза радиационной обстановки и оценки доз облучения при авариных ситуациях с выходом радиоактивности в атмосферу. Использование экспериментальных данных для уточнения результатов моделирования переноса радиоактивности в атмосфере может улучшить точность оценок содержания радионуклидов в окружающей среде и доз облучения населения. Для определения параметров измерительного оборудования, исследования возможности идентификации и определения активности радионуклидов в облаке выброса наиболее универсальным способом является применение математического моделирования, в то время как в силу специфики рассматриваемых задач проведение экспериментальных исследований является крайне затруднительным. ИБРАЭ РАН имеет многолетний опыт по решению задач атмосферного переноса, в том числе с помощью программного комплекса «Нострадамус» [2, 3] на основе лагранжевой стохастической траекторной модели, использование результатов определения содержания радио-

нуклидов в облаке выброса может позволить проводить моделирование аппаратурных спектров детекторов гамма-излучения с учётом сложной формы облака выброса и вариаций метеорологических условий.

В настоящей работе представлено описание подхода для моделирования аппаратурных спектров гамма-излучения от облака выброса произвольной формы, приведены результаты применения данного способа для расчёта спектров сцинтилляционного детектора с использованием упрощённой модели облака выброса. Результаты работы позволят осуществлять выбор параметров оборудования, измерений, способов обработки измерений для повышения точности прогнозов доз облучения, проводимых с помощью расчётных кодов по моделированию распространения радионуклидов в воздухе.

Материалы и методы

Для решения задачи моделирования аппаратурных спектров от облака выброса необходимо представление облака как источника гамма-излучения. В качестве упрощённого описания облака выброса широко используется гауссова модель [4], при определённых приближениях в задачах, связанных с определением характеристик поля излучения, применяются модели облака в виде линейного источника и бесконечного полупространства [4, 5]. Однако, как показывает опыт проведения расчётов распространения радионуклидов в атмосфере с помощью программного комплекса «Нострадамус» [2], основанного на лагранжевой модели атмосферного переноса, с использованием модели WRF для определения метеорологических параметров, облако выброса может иметь достаточно сложную форму. В связи с этим, наиболее универсальным подходом можно считать представление облака в виде совокупности элементарных источников, каждый из которых можно было бы считать точечным.

В результате в рамках проведённых работ была разработана процедура расчёта аппаратурных спектров, состоящая из нескольких этапов:

• •    расчёт энергетического распределения плотности потока в точке расположения детектора на основе данных для точечных источников;

• •    определение аппаратурного спектра детектора с использованием результатов первого этапа и рассчитанных аппаратурных спектров от единичного потока излучения, падающего на детектор.

Преимуществами такой последовательности решения общей задачи моделирования аппаратурных спектров являются относительная простота задач каждого этапа и, в случае использовании метода Монте-Карло, как, например, в данной работе, возможность их эффективного решения с точки зрения минимизации времени на подготовку исходных данных и проведение расчётов. Кроме того, выполнив однократно расчёты первого этапа, данная процедура обеспечивает возможность их многократного использования для проведения вычислений с различными детекторами. Таким образом, для каждого нового детектора потребуется проведение только второго этапа расчёта.

Первый этап включает в себя определение плотности потока от облака выброса в предполагаемой точке расположения детектора на основе заданного разбиения облака на элементарные источники и предварительно выполненных расчётов энергетического распределения плотности потока от точечных изотропных источников гамма-излучения для различных расстояний и значений энергии источника. Для исследований, проведённых в рамках данной работы, определение энергетического распределения плотности потока от точечного изотропного источника проводилось с помощью метода Монте-Карло [6-9] в сферической геометрии, использовалась оценка плотности потока по пересечениям. Энергетическое распределение плотности потока рассчитывалось на определённой сетке по энергии источника и расстоянию от источника до точки детектирования. Предполагалось, что сетка по расстоянию включает в себя значения до 1 км, в то время как сетка по энергии охватывает диапазон от 100 до 3000 кэВ, в котором находится основная часть гамма-линий известных радионуклидов.

В случае, когда между источником и детектором находится слой материала большой толщины (условно более 5-7 длин свободного пробега гамма-излучения в данной среде), проведение вычислений методом Монте-Карло сталкивается с известными трудностями [10, 11], что требует применения дополнительных мер, к числу которых можно отнести применение методов уменьшения дисперсии. В воздухе длина свободного пробега гамма-излучения с энергией в диапазоне от 100 до 3000 кэВ составляет десятки и сотни метров [12], этим было обусловлено использование в расчётах плотности потока методов «геометрическое расщепление» и «русская рулетка» с разбиением геометрии на слои размером порядка 1 длины свободного пробега, каждому из которых сопоставлялись значения ценностей. При выборе значений ценностей учитывались рекомендации, содержащиеся в работах [10, 11].

Чтобы избежать вычислений для слишком большого числа гамма-линий радионуклидов, которые потенциально могут содержаться в облаке выброса, был принят подход, в соответствии с которым первоначально производятся расчёты энергетического распределения плотности потока для набора значений энергий (узлов сетки), охватывающего диапазон от 100 до 3000 кэВ, затем на основе этих данных методом интерполяции определяется вклад для каждой гамма-линии с последующим суммированием вкладов ото всех гамма-линий данного нуклида. Имея результаты расчёта энергетического распределения плотности потока на заданной сетке по энергии источника, путём интерполяции можно получать необходимые результаты для любого радионуклида со сколь угодно сложным энергетическим составом гамма-излучения. Данные о характеристиках излучения радионуклидов, включая энергию и выход излучения на распад, могут быть взяты из соответствующих публикаций МКРЗ, в настоящей работе использовались данные публикации 38 МКРЗ [13], на основе которых получена большая часть доступных и широко применяемых при моделировании последствий аварий данных для оценки доз облучения. Расчёт плотности потока на заданной сетке по энергии источника с последующей интерполяцией позволит обеспечить независимость процедуры моделирования спектров от радионуклидного состава облака выброса.

При интерполяции энергетического распределения плотности потока по энергии источника возникают определённые трудности, так как с изменением энергии источника происходит смещение и изменение размера отдельных областей и элементов структуры плотности потока по энергетической шкале. При этом изменение компонентов структуры, таких как пик нерассеянного излучения, комптоновский континуум, комптоновский край, пик аннигиляционных гамма-квантов имеет различный характер зависимости от энергии источника. Таким образом, применение прямой интерполяции между энергетическими группами с одинаковыми номерами невозможно. В связи с этим, с учётом анализа имеющихся опубликованных данных [14-16], в которых рассматривается более сложная задача интерполяции функции отклика детектора, было решено использовать алгоритм, основанный на разбиении энергетического распределения плотности потока на несколько областей по энергии, в каждой из которых интерполяция производится отдельно. Разбиение на такие энергетические диапазоны производится с учётом особенностей структуры плотности потока. В качестве границ диапазонов, перемещаясь влево по шкале энергии, могут быть взяты: пик, соответствующий нерассеянному излучению; край комптоновского рассеяния; максимум в левой части распределения. Ширина таких энергетических диапазонов различна для энергетических распределений плотности потока, соответствующих различным значениям энергии источника. При интерполяции в пределах данного диапазона производится разбиение энергетических распределений плотности потока для соседних значений сетки по энергии источника на одинаковое количество виртуальных энергетических групп, после чего интерполяция в данном диапазоне производится обычным образом (например, линейная интерполяция по энергии источника или интерполяция в логарифмическом масштабе по шкале энергии источника), используя значения плотности потока в соответствующих виртуальных группах.

Обработка пика аннигиляционных гамма-квантов, который можно наблюдать в структуре энергетического распределения плотности потока при энергиях источника выше 1022 кэВ, производится отдельно. Первоначально во всех рассчитанных энергетических распределениях плотности потока для точечных источников выделяются пики аннигиляционных гамма-квантов, их значения хранятся и интерполируются отдельно. После выполнения процедуры интерполяции пиков полученное значение плотности потока в соответствующей энергетической группе (с энергией 511 кэВ) прибавляется к остальной части энергетического распределения плотности потока. Для определения значения плотности потока в энергетической группе, соответствующей энергии источника, интерполяция не используется, плотность потока в этом случае определяется с помощью известного аналитического выражения для точечного изотропного источника [9]. Необходимые в этом случае данные по коэффициентам ослабления гамма-излучения для воздуха в диапазоне энергий 100-3000 кэВ с хорошей точностью описываются зависимостью, обратной квадратному корню из полинома второй степени.

Так как с изменением расстояния от источника структура энергетического распределения плотности потока остаётся постоянной, для определения плотности потока в промежуточных точках сетки по расстоянию может быть использован обычный алгоритм интерполяции по значениям в группах с одинаковыми порядковыми номерами.

После того, как определено энергетическое распределение плотности потока в точке расположения детектора, становится возможным проведение расчётов аппаратурных спектров на основе предварительно полученной функции отклика детектора, нормированной на единичную плотность потока падающего на детектор излучения, путём операции свертки:

G(E-) = ^™“д(Е,Е').ф(Е') dE', где д(Е,Е') - функция отклика детектора для единичного потока гамма-излучения с энергией Е'; <(Е') - энергетическое распределение плотности потока в точке расположения детектора; Emax - максимальное значение энергии, в данной работе Emax=3000 кэВ.

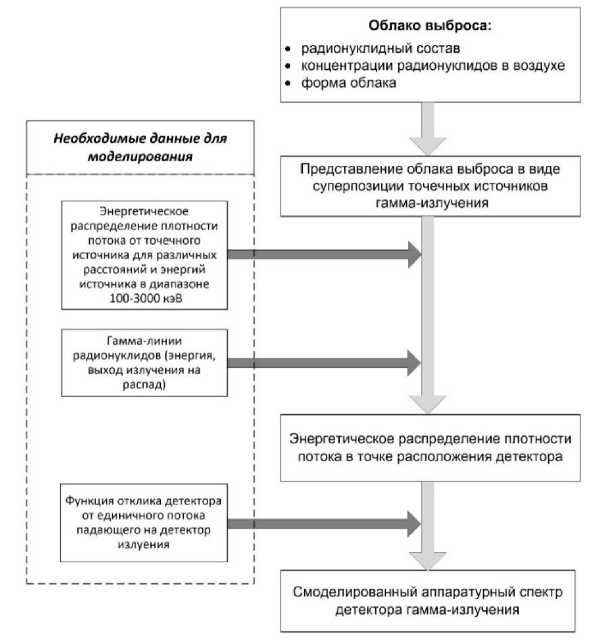
Рис. 1. Схема процедуры расчёта аппаратурных спектров детекторов от гамма-излучения радионуклидов, содержащихся в облаке выброса.

В целом последовательность расчёта аппаратурных спектров с указанием основных этапов и необходимых расчётных данных представлена на рис. 1. Данный способ моделирования аппаратурных спектров является универсальным по отношению к радионуклидному составу облака выброса и позволяет с достаточной степенью оперативности осуществлять расчёты спектров для различных детекторов, используя заранее рассчитанные данные при облучении детектора единичным потоком гамма-излучения с энергией в диапазоне от 100 до 3000 кэВ.

Результаты и обсуждение

С целью реализации выбранного подхода к моделированию аппаратурных спектров от облака выброса были проведены расчёты энергетического распределения плотности потока от точечного изотропного источника гамма-излучения для различных расстояний и энергий источника. Расчёты проводились с помощью метода Монте-Карло с применением методов уменьшения дисперсии «геометрическое расщепление» и «русская рулетка» [10, 11]. Модель геометрии расчёта предполагала, что источник и точка определения плотности потока находятся в бесконечной среде, заполненной воздухом. Для применения методов уменьшения дисперсии геометрия разбивалась на слои толщиной в одну длину свободного пробега, соответствующую энергии гамма-излучения источника, и менее, каждому слою ставилось в соответствие значение ценностей, руководствуясь подходами, описанными в [10, 11]. Это дало возможность провести расчёты для расстояний до 10 и более длин свободного пробега.

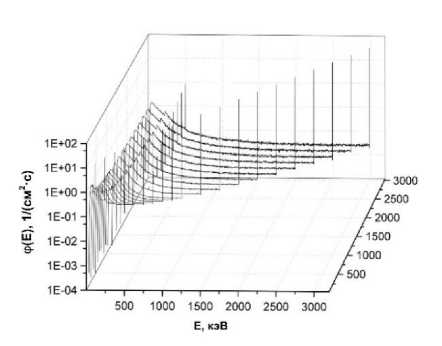
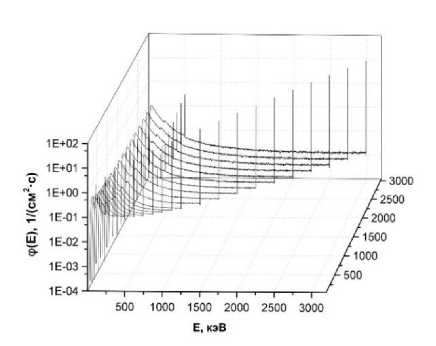
Результаты определения энергетического распределения плотности потока были получены на заранее заданной сетке по расстоянию и энергии источника. Сетка по энергии источника E включает в себя значения от 100 до 3000 кэВ с шагом, варьирующимся от 10 до 50 кэВ: 10 кэВ - E<500 кэВ, 20 кэВ - E<1000 кэВ и 50 кэВ - E<3000 кэВ. Из соображений компромисса между объёмом необходимых вычислений и минимизацией ошибки применения интерполяции выбраны следующие значения расстояний от источника до точки определения плотности потока: 10, 25, 50 м и далее с шагом 25 м до 1000 м. Было проведено сравнение результатов определения энергетического распределения плотности потока в точках, являющихся серединами интервалов сетки по энергии и расстоянию, путём интерполяции и с помощью непосредственного расчёта методом Монте-Карло. В результате получено, что указанные выше параметры сетки обеспечивают значение среднеквадратичной ошибки на уровне менее 10% в серединных точках интервалов для большей части рассматриваемого диапазона энергий источника и расстояний от источника до точки детектирования. На рис. 2а и 2б представлены полученные энергетические распределения плотности потока от точечного изотропного источника активно- стью 1 Ки для расстояний 75 и 100 м.

а

Рис. 2. Энергетические распределения плотности потока от точечного источника гамма-излучения активностью 3,7·10¹⁰ Бк для расстояний 75 (а) и 125 (б) и энергий источника от 100 до 3000 кэВ.

б

На основе этих данных были смоделированы аппаратурные спектры сцинтилляционного детектора NaI 063x63 мм для упрощённой модели облака выброса в виде бесконечного линейного источника с равномерным распределением активности по длине. Для определения аппаратурных спектров предварительно был проведён расчёт функции отклика детектора NaI 063x63 мм при облучении его плоскопараллельным потоком гамма-излучения с энергией от 100 до 3000 кэВ с шагом 1 кэВ. Линейный источник представлялся как совокупность элементарных точечных источников. Разбиение на элементы производилось таким образом, чтобы размер элемента был существенно меньше расстояния до точки детектирования. Как показали проведённые оценки, при использовании критерия регистрации 90% плотности потока [17, 18] для определения условно бесконечного размера L линейного источника c учётом процессов взаимодействия излучения с воздухом справедливо соотношение: 0,5 ■ L > d, где d- кратчайшее расстояние до источника. Используя данные приближения, были рассчитаны аппаратурные спектры детектора NaI 063x63 мм для расстояний до 600 м от линейного источника активностью 1 Бк/см. Данные о гамма-линиях радионуклидов брались из публикации 38 МКРЗ [13], расчёты спектров были проведены для всех 838 радионуклидов, информация о которых содержится в данной публикации. В расчётах не учитывались гамма-линии, вклад которых в выделяемую на один акт распада энергию составлял менее 10% от суммарного вклада всех гамма-линий радионуклида. В качестве примера, некоторые результаты моделирования спектров для значимых гамма-излучателей, которые могут присутствовать в воздухе вследствие выброса на АЭС, представлены на рис. 3.

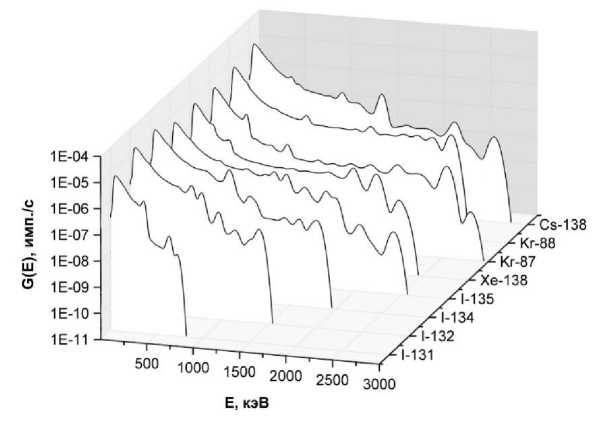
Рис. 3. Рассчитанные аппаратурные спектры детектора NaI 063x63 мм на расстоянии 120 м от линейного источника активностью 1 Бк/см.

Выводы

В результате проведённых исследований в рамках совершенствования концепции гибридного мониторинга был разработан подход, позволяющий проводить моделирование аппаратурных спектров детекторов гамма-излучения для облака выброса произвольной формы с различным радионуклидным составом. Представленный способ моделирования также обладает свойствами универсальности по отношению к выбору типа детектора и его энергетического разрешения для проведения расчётов. Решение задачи определения аппаратурных спектров при прохождении облака выброса расчётным путём может быть использовано при исследовании возможностей детектирования радионуклидов в облаке с помощью проведения наземных измерений с конечной целью восстановления источника выброса и использования этих данных для проведения прогнозов радиационной обстановки. В случае реализации концепции гибридного мониторинга, информация, получаемая после обработки результатов измерений, будет использоваться для повышения точности проводимого с помощью расчётных программ по моделированию распространения радионуклидов в атмосфере прогнозов доз облучения населения. Описанный в настоящей работе подход был опробован на задаче определения спектров сцинтилляционного детектора для приближенной модели облака в виде бесконечного линейного источника, получены аппаратурные спектры для расстояния от источника до 600 м и всех радионуклидов, данные о гамма-излучении которых содержатся в публикации 38 МКРЗ. Полученные результаты могут быть использованы для проведения быстрых оценок, при этом возможно более широкое применение подхода к моделированию аппаратурных спектров, в том числе для расчётов, когда облако выброса имеет произвольную форму. Также в рамках развития существующего подхода планируются дальнейшие работы по моделированию различных сценариев аварийных ситуаций на АЭС с помощью программного комплекса «Нострадамус».