Задача о бесконечной пластине, нагруженной нормальной силой, движущейся по сложной траектории

Введение. Исследование динамических явлений, обусловленных действием подвижной нагрузки, представляет собой актуальную задачу, имеющую прикладное значение (например, при решении вопросов развития транспорта). В работах, посвященных указанной проблеме, рассматривались различные задачи с подвижной нагрузкой. В частности, показано, как на полуплоскость или полупространство (упругое изотропное, трансверсальное изотропное, вязкоупругое) действует нагрузка, движущаяся по бесконечной прямой линии с постоянной скоростью. В этом случае при решении задачи вводится подвижная система координат, связанная с движущейся силой, что позволяет исключить время из числа независимых переменных [1–5]. Часть работ посвящена изучению действия на бесконечную пластину или полосу (упругую или вязкоупругую) равномерно движущейся по прямолинейной траектории нагрузки. При этом используется тот же метод исключения временной переменной или рассматривается квазистатическая постановка задачи [6–12]. Наибольший интерес представляют задачи, в которых длина траектории движения нагрузки конечна, а сама траектория представляет собой кривую линию. Часто этом случае используется конечноэлементное моделирование движущейся нагрузки [11– 13]. В ряде работ при решении подобных задач используются вариационные методы (в частности метод Рэлея — Ритца) [14–16] или разновидность метода Галеркина, позволяющая сводить задачу к обыкновенным дифференциальным уравнениям. При этом рассматриваются разнообразные объекты приложения подвижной нагрузки (плиты, слоистые плиты, вязкоупругие плиты, полупространства — как изотропные, так и анизотропные) [17–19]. В данной статье представлен метод, который развивает идеи, изложенные в работах [20–23].

Материалы и методы. Рассмотрим бесконечную пластину, лежащую на упругом винклеровском основании, которая находится под действием нормально приложенной силы, перемещающейся по замкнутой траек- тории.

Задача сводится к интегрированию уравнения движения пластины, лежащей на упругом винклеровском основании [14]:

где W — прогиб пластины; D =

Eh ³

12(1 -v ²)

; Е — модуль Юнга; v — коэффициент Пуассона; h — толщина пла

стины; с 2 =”; Р — плотность материала; k = ^; K — коэффициент податливости упругого основания; P — сосредоточенная сила, движущаяся по замкнутой кривой у с постоянной скоростью a.

Введем координату 5 , отсчитываемую от некоторой фиксированной точки кривой у . Тогда сила P , движущаяся вдоль кривой у со скоростью a , будет описываться соотношением P = P ( 5 - at ). Функция P ( 5 - at )

периодическая по t , c периодом T = —, где L — длина кривой у .

Решение. Рассмотрим установившийся режим. Разложим функцию P(5 - at) в ряд Фурье по перемен- ной t на отрезке

L ; L 2 a ; 2 a

В этом случае коэффициенты разложения предстанут виде:

Механика

L

/2 a              _ ,   ,

2 iak п t/ ck =     P(s — at)e    Ld dt.

• — L

Сделав замену переменной интегрирования в интеграле 5 — at = z , получим:

L

2 ik пs/           2 ik ns/ eLeL

= d—k        , aa

/2       _  /

• — 2 ik nz/

с_к = I P ( z ) e     L d dz

L

/2

где d k — коэффициенты разложения в ряд Фурье на отрезке

LL ---

2 2

функции P ( z ).

Тогда подвижную нагрузку можно представить в виде ряда Фурье:

1      _?         2 ik п ( 5 — at )

P ( 5 — at ) = — / d - _ke      ^z

a к=—^

Учитывая линейность задачи, ее решение можно представить в виде:

то w = £ d-kWк ,

•

к=—то где Wk — прогибы пластины, обусловленные действием вертикальной нагрузки, распределение которой вдоль

кривой у описывается функцией e L^L , изменяющейся во времени по закону e

•

Для определения W k воспользуемся фундаментальным решением уравнения (1), которое соответствует P = 8 ( x — Х о ) 8 ( у — у о )e " ^{1 ю} k t , где ® k = 2^ .

Используя принцип предельного поглощения и традиционные методы построения решений дифферен- ш 2 циальных уравнений, можно получить фундаментальное решение уравнения (1), которое при к > у- имеет c

вид:

w k ⁽ x , У , x o , У о ) =

"A-[ K о ( a R ) — K о ( a2 R ) ] , 4 ns D

где R = 1 ( x ^— x o ) ² + ( У ^— У о ) ² I 2 , ^s

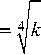
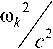
i n              — i П a, = se /4, a1 = se /4, Kо (z) — функция Макдональда.

^юк ²  _{a Q a} _

При k < -у- решение имеет вид:

c

w k ⁽ x , У , ^х о , У о ) =

-4- ^Н о¹) ( y r ) — K о ( Y R ) , 4 пу D L 2                  J

/     2

где Y = ⁴   k 2— k , Н Q1) ( y R ) — функция Ганкеля.

V c²

Тогда W k = ф W k ( x , У , Х о ( s ), У о ( s )) e

^L ds . Используя известные формулы теории тонких пластин и

Y полученную по приведенным выше соотношениям формулу, определяющую прогиб W (2), можно вычислить перемещения ux, иУ и напряжения ax, аУ и аХУ в любой точке пластины.

При больших k приходится вычислять интеграл от быстро осциллирующих функций. Для этого использовалась квадратурная формула, основанная на замене кубическим сплайном слабо осциллирующей части

2 ik пs подынтегральной функции, а сильно осциллирующий множитель e  LL рассматривался как весовая функ-

ция [15].

Результаты исследования. Итак, бесконечная пластина лежит на упругом винклеровском основании.

На нее действует нормальная сила, перемещающаяся по траектории, изображенной на рис 1.

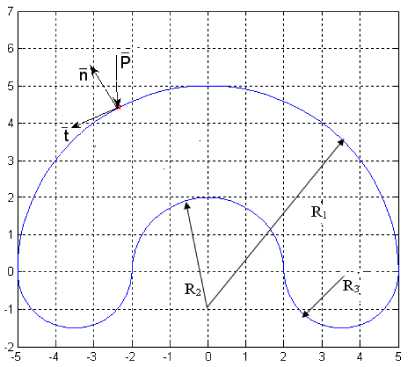
Рис. 1. Траектория движения нагрузки

Расчеты проводились при следующих исходных данных: h = 0,25 м; с = 221 м/c; E = 2324694 0 H /м²; v = 0,36 . На рис. 2 приведены результаты расчетов, соответствующие K = 1,864 м”⁴ и a = 125м/с.

x 10-8

-500

-1000

t

-1500

-2000

-2500

-5

IF

г

Stt

Snt

Sntt

-500

-2000

-2500

5    -5

X....

Н

t

Stn

Snn

Sntn

Рис. 2. Изменение перемещений и напряжений

Данные графики описывают изменения перемещений и напряжений в системе координат, связанной с точкой приложения движущейся силы Р . Ось t направлена по касательной к траектории движения t , а ось n — по внешней нормали к области, ограниченной траекторией n (см. рис. 1) при z = h 2 .

При этом вектор перемещений и тензор напряжений соответственно представлялись в виде

Механика

U = Ut • t + Un • n + W • k , S = St • tt + Sn • nn + Stn • ( tn + nt ) , где k — нормаль к пластине.

На рис. 2 показано изменение вдоль оси t компонент вектора перемещений Wt , Utt , Unt , тензора напряжений Stt , Snt , Stnt и изменение этих величин вдоль оси n — Wn , Utn , Unn и Stn , Snn , Stnn .

Согласно расчетам, характер поведения указанных величин во всех точках траектории остается неизменным. Расчеты показали также, что при изменении скорости движения нагрузки а в пределах от 0 до 125 м/с компоненты вектора перемещений и тензора напряжений возрастали незначительно (на 3-4%).

Для изучения распространения энергии упругих волн вычислялись компоненты вектора Умова - Пой-тинга e i = - S ij ⋅∂ t u i ( S ij — компоненты тензора напряжений, u i — координаты вектора перемещений), направление которого указывает направление распространения энергии, а длина описывает количество энергии, переносимое через единицу поверхности, перпендикулярной к направлению данного вектора в единицу времени.

На рис. 3. представлено распространение энергии упругих волн около движущейся сосредоточенной силы (положение силы обозначено красной звездочкой).

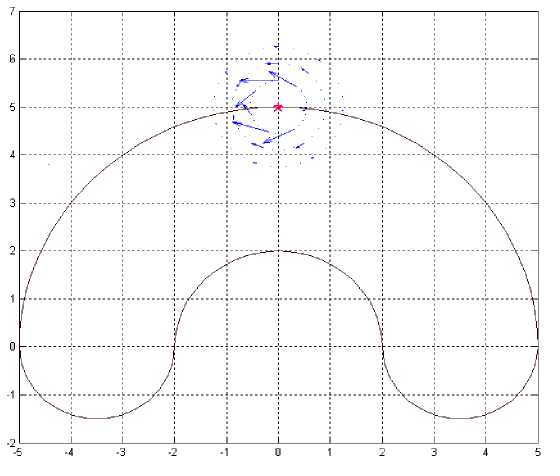
Рис. 3. Распространение энергии упругих волн

Обсуждение и заключения. Анализ полученных результатов показывает, что при указанных выше пределах изменения скорости длина вектора Умова - Пойтинга практически пропорциональна скорости движения нагрузки и качественная картина распространения энергии вблизи силы слабо изменяется в процессе движения. Характер поведения рассчитанных выше перемещений и напряжений во всех точках траектории остается неизменным, а их значения слабо зависят от скорости движения нагрузки a при изменении этой скорости в пределах от 0 до 125 м/c .

Применение предложенного метода к бесконечной пластине, лежащей на упругом основании, не исчерпывает его возможности. Он может быть использован при рассмотрении более сложных объектов (плиты сложной формы, слоистые плиты, вязкоупругие плиты). Рассмотренный метод отличается от упомянутых выше большей экономичностью, так как использует для построения решения уже известные решения задач. Окончательное решение выражается в удобном виде — как сумма криволинейных интегралов.

Полученные результаты могут быть использованы в процессе проектирования дорог. Изучение распространения энергии упругих волн от движущихся транспортных средств позволит оценить воздействие указанных волн на строения, расположенные вблизи дороги. С учетом данных о характере изменения перемещений и напряжений оценивается износ дорожного покрытия.

Библиографический список